标签:迷宫问题 val 方向 arch 记录 next com lag ext
广度优先搜索
1.算法的基本思路
算法设计的基本步骤为:
1)确定图的存储方式;
2)图的遍历过程中的操作,其中包括为输出问题解而进行的存储操作;
3)输出问题的结论。
2.算法框架
从广度优先搜索定义可以看出活结点的扩展是按先来先处理的原则进行的,所以在算法中要用“队”来存储每个E-结点扩展出的活结点。为了算法的简洁,抽象地定义:
queue为队列类型,
InitQueue( ) 为队列初始化函数,
EnQueue(Q,k)为入队函数,
QueueEmpty(Q) 为判断队空函数,
DeQueue(Q) 为出队函数。
实际应用中,用数组或链表实现队列。
开辟数组visited记录visited结点的搜索情况。
在算法框架中以输出结点值表示“访问”。
1)邻接表表示图的广度优先搜索算法
int visited[n]; /n 为结点个数/
bfs(int k,graph head[])
{int i; queue Q ; edgenode *p; /定义队列/
InitQueue(Q); /队列初始化/
print(“visit vertex”,k); / 访问源点vk/
visited[k]=1;
EnQueue(Q,k);
/vk已访问,将其入队。/
while(!QueueEmpty(Q)) /队非空则执行/
{ i=DeQueue(Q);
/ vi出队为E-结点/
p=head[i].firstedge; /取vi的边表头指针/
while(p<>null) /扩展E-结点 /
{if(visited[p->adjvex]=0) /若vj未访问过/
{ print (“visitvertex”,p->adjvex);/访问vj/
visited[p->adjvex]=1;
EnQueue(Q,p->adjvex);} /访问过的vj人队/
p=p->next ; } /找vi的下一邻接点/
}
2)邻接矩阵表示的图的广度优先搜索算法
bfsm(int k, graph g[][100],int n)
{int i,j;
CirQueue Q; InitQueue(Q);
print ("visit vertex", k); /访问源点vk/
visited[k]=1;
EnQueue(Q,k);
while(not QueueEmpty(Q))
{i=DeQueue(Q); /vi出队/
for(j=0;j<G->n;j++) /扩展结点/
if(g[i][j]==1 and visited[j]=0)
{print("visit
vertex",j);
visited[j]=1;
EnQueue(Q,j);} /访问过的vj人队/
}
}
广度优先搜索的应用
【例1】已知若干个城市的地图,求从一个城市到另一个城市的路径,要求路径中经过的城市最少。
算法设计:
图的广度优先搜索类似与树的层次遍历,逐层搜索正好可以尽快找到一个结点与另一个结点相对而言最直接的路径。
如图5-6表示的是从城市A到城市H的交通图。从图中可以看出,从城市A到城市H要经过若干个城市。现要找出一条经过城市最少一条路线。
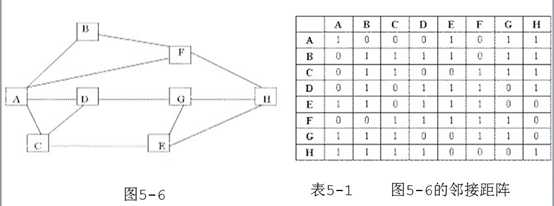
具体过程如下:
1)将城市A(编号1)入队,队首qh置为0、队尾qe置为1。
2)将队首所指的城市所有可直通的城市入队(如果这个城市在队中出现过就不入队),然后将队首加1,得到新的队首城市。重复以上步骤,直到城市H入队为止。当搜到城市H时,搜索结束。
3)输出最少城市线路。
数据结构设计:
1)线性数组a作为活结点队的存储空间。
2)队列的每个结点有两个成员:a[i].city记录入队的城市,a[i].pre记录该城市的前趋城市在队列中的下标,这样通过a[i].pre就可以倒推出最短线路。
3)设置数组visited[]记录已搜索过的城市。
算法如下:
int jz[8][8]= {{1,0,0,0,1,0,1,1},{0,1,1,1,1,0,1,1}, {0,1,1,0,0,1,1,1}, {0,1,0,1,1,1,0,1}, {1,1,0,1,1,1,0,0},{0,0,1,1,1,1,1,0}, {1,1,1,0,0,1,1,0}, {1,1,1,1,0,0,0,1}};
struct {int city, pre;} sq[100];
int qh,qe,i,visited[100];
main( )
{int i,n=8;
for(i=1;i<=n,i=i+1) visited[i]=0;
search( );
}
search( )
{qh=0; qe=1;sq[1].city=1;sq[1].pre=0;visited[1]=1;
while( qh<>qe) /当队不空/
{qh=qh+1; /结点出队/
for(i=1;i<=n,i++) /扩展结点/
if (jz[sq[qh].city][i]=1 and visited[i]=0)
{ qe=qe+1; /结点入队/
sq[qe].city=i;sq[qe].pre=qh;visited[qe]=1;
if (sq[qe].city=8) out( );
}
}
print(“No avaliable way.”);
}
out( ); /输出路径/
{print(sq[qe].city);
while(sq[qe].pre<>0)
{qe=sq[qe].pre;
print(‘--‘,sq[qe].city);}
}
算法分析:时间复杂度是O(n);空间复杂性为(n2),包括图本身的存储空间和搜索时辅助空间“队”的存储空间。
【例2】走迷宫问题
迷宫是许多小方格构成的矩形,在每个小方格中有的是墙(图中的“1”)有的是路(图中的“0”)。走迷宫就是从一个小方格沿上、下、左、右四个方向到邻近的方格,当然不能穿墙。设迷宫的入口是在左上角(1,1),出口是右下角(8,8)。根据给定的迷宫,找出一条从入口到出口的路径。
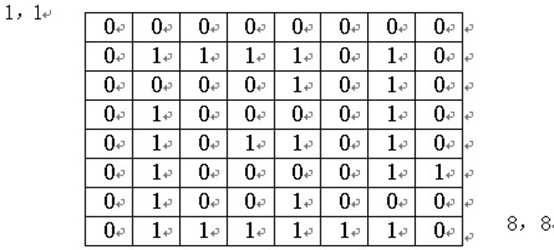
算法设计:
从入口开始广度优先搜索可到达的方格入队,再扩展 队首的方格,直到搜索到出口时算法结束。
对于迷宫中任意一点A(Y,X),有四个搜索方向:
向上A(Y-1,X)
向下A(Y+1,X)
向左A(Y,X-1)
向右A(Y,X+1)
当对应方格可行(值为0),就扩展为活结点。
数据结构设计:
用数组做队的存储空间,队中结点有三个成员:行号、列号、前一个方格在队列中的下标。搜索过的方格不另外开辟空间记录其访问的情况,而是用迷宫原有的存储空间置元素值为“-1”时,标识已经访问过该方格。
为了构造循环体,用数组fx={1,-1,0,0}、fy={ 0,0,-1,1 }模拟上下左右搜索时的下标的变化过程。
算法如下:
int maze[8][8]= {{0,0,0,0,0,0,0,0},{0,1,1,1,1,0,1,0}, {0,0,0,0,1,0,1,0},{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},
{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},{0,1,1,1,1,1,1,0}};
int fx[4]={1,-1,0,0}, fy[4]={ 0,0,-1,1 }; //下标起点为1
struct {int x,y, pre;}sq[100];
int qh,qe,i,j,k;
main( )
{
search( );
}
search( )
{qh=0;qe=1;maze[1][1]=-1;
sq[1].pre=0; sq[1].x=1; sq[1].y=1;
while( qh<>qe) /当队不空/
{qh=qh+1; /出队/
for(k=1;k<=4;k=k+1) /搜索可达的方格/
{i=sq[qh].x+fx[k]; j=sq[qh].y+fy[k];
if (check(i,j)=1)
{ qe=qe+1; sq[qe].x=i; sq[qe].y=j; /入队/
sq[qe].pre=qh; maze[i][j]=-1;
if (sq[qe].x=8 and sq[qe].y=8)
{out( );return;} }}
print(“Non solution.”);}
check(int i,int j)
{int flag=1;
if(i<1 or i>8 or j<1 or j>8) flag=0; /是否在迷宫内/
if(maze[i][j]=1 or maze[i][j]=-1) flag=0; /是否可行/
return(flag);
}
out( ) /输出过程/
{print(“(”,sq[qe].x,”,” sq[qe].y,”)”);
while(sq[qe].pre<>0)
{ qe=sq[qe].pre;
print(‘--‘, “(”,sq[qe].x,”,” sq[qe].y,”)”);}
}
标签:迷宫问题 val 方向 arch 记录 next com lag ext
原文地址:https://www.cnblogs.com/gd-luojialin/p/10384714.html