标签:width oca type 不用 概率 元素 链式 数字分析 没有
查找表:
由同一类型的数据元素(或记录)构成的集合
静态查找表:
查找的同时对查找表不做修改操作(如插入和删除)
动态查找表:
查找的同时对查找表具有修改操作
关键字
记录中某个数据项的值,可用来识别一个记录
主关键字:
唯一标识数据元素
次关键字:
可以标识若干个数据元素
查找算法的评价指标
关键字的平均比较次数,也称平均搜索长度ASL(Average Search Length)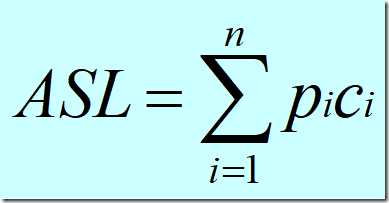
n:记录的个数
pi:查找第i个记录的概率 ( 通常认为pi =1/n )
ci:找到第i个记录所需的比较次数
应用范围:
顺序表或线性链表表示的静态查找表
表内元素之间无序
顺序表的表示
typedef struct { ElemType *R; //表基址 int length; //表长 }SSTable;
第2章在顺序表L中查找值为e的数据元素
int LocateELem(SqList L,ElemType e) { for (i=0;i< L.length;i++) if (L.elem[i]==e) return i+1; return 0;}
改进:把待查关键字key存入表头(“哨兵”),从后向前逐个比较,可免去查找过程中每一步都要检测是否查找完毕,加快速度。
int Search_Seq( SSTable ST , KeyType key ){ //若成功返回其位置信息,否则返回0 ST.R[0].key =key; for( i=ST.length; ST.R[ i ].key!=key; - - i ); //不用for(i=n; i>0; - -i) 或 for(i=1; i<=n; i++) return i; }
顺序查找的性能分析:
空间复杂度:一个辅助空间。
时间复杂度:
1) 查找成功时的平均查找长度
设表中各记录查找概率相等
ASLs(n)=(1+2+ ... +n)/n =(n+1)/2
2)查找不成功时的平均查找长度 ASLf =n+1
顺序查找算法有特点:
算法简单,对表结构无任何要求(顺序和链式)
n很大时查找效率较低
改进措施:非等概率查找时,可按照查找概率进行排序。
若k==R[mid].key,查找成功
若k<R[mid].key,则high=mid-1
若k>R[mid].key,则low=mid+1
设表长为n,low、high和mid分别指向待查元素所在区间的上界、下界和中点,k为给定值
初始时,令low=1,high=n,mid=?(low+high)/2?
让k与mid指向的记录比较
若k==R[mid].key,查找成功
若k<R[mid].key,则high=mid-1
若k>R[mid].key,则low=mid+1
重复上述操作,直至low>high时,查找失败
int Search_Bin(SSTable ST,KeyType key){ //若找到,则函数值为该元素在表中的位置,否则为0 low=1;high=ST.length; while(low<=high){ mid=(low+high)/2; if(key==ST.R[mid].key) return mid; else if(key<ST.R[mid].key) high=mid-1;//前一子表查找 else low=mid+1; //后一子表查找 } return 0; //表中不存在待查元素 }
折半查找的性能分析:
查找过程:每次将待查记录所在区间缩小一半,比顺序查找效率高,时间复杂度O(log2 n)
适用条件:采用顺序存储结构的有序表,不宜用于链式结构
分块有序,即分成若干子表,要求每个子表中的数值都比后一块中数值小(但子表内部未必有序)。
然后将各子表中的最大关键字构成一个索引表,表中还要包含每个子表的起始地址(即头指针)。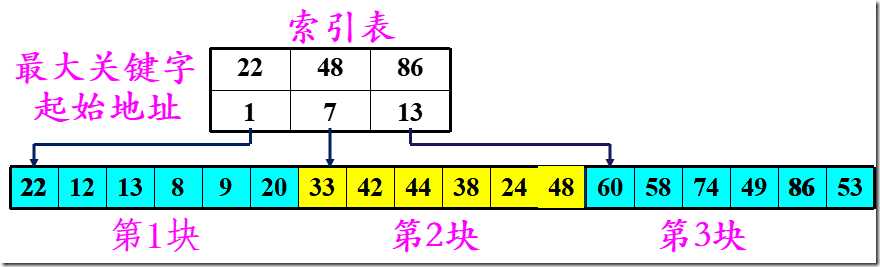
① 对索引表使用折半查找法(因为索引表是有序表);
② 确定了待查关键字所在的子表后,在子表内采用顺序查找法(因为各子表内部是无序表);
分块查找性能分析:
优点:插入和删除比较容易,无需进行大量移动。
缺点:要增加一个索引表的存储空间并对初始索引表进行排序运算。
适用情况:如果线性表既要快速查找又经常动态变化,则可采用分块查找。
二叉排序树
平衡二叉树
B-树
B+树
键树
二叉排序树或是空树,或是满足如下性质的二叉树:
(1)若其左子树非空,则左子树上所有结点的值均小于根结点的值;
(2)若其右子树非空,则右子树上所有结点的值均大于等于根结点的值;
(3)其左右子树本身又各是一棵二叉排序树
得到一个关键字的递增有序序列
(1)若二叉排序树为空,则查找失败,返回空指针。
(2)若二叉排序树非空,将给定值key与根结点的关键字T->data.key进行比较:
① 若key等于T->data.key,则查找成功,返回根结点地址;
② 若key小于T->data.key,则进一步查找左子树;
③ 若key大于T->data.key,则进一步查找右子树。
BSTree SearchBST(BSTree T,KeyType key) { if((!T) || key==T->data.key) return T; else if (key<T->data.key) return SearchBST(T->lchild,key); //在左子树中继续查找 else return SearchBST(T->rchild,key); //在右子树中继续查找 } // SearchBST
若二叉排序树为空,则插入结点应为根结点
否则,继续在其左、右子树上查找
树中已有,不再插入
树中没有,查找直至某个叶子结点的左子树或右子树为空为止,则插入结点应为该叶子结点的左孩子或右孩子
插入的元素一定在叶结点上
从空树出发,经过一系列的查找、插入操作之后,可生成一棵二叉排序树
将因删除结点而断开的二叉链表重新链接起来
防止重新链接后树的高度增加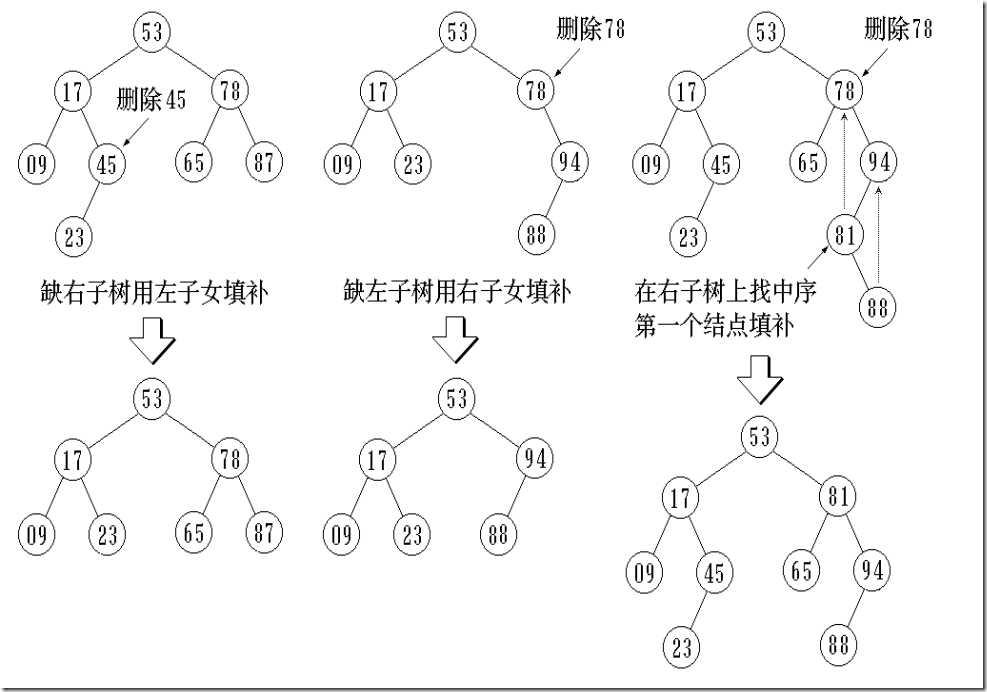
查找的性能分析:
平均查找长度和二叉树的形态有关,即,
最好:log2n(形态匀称,与二分查找的判定树相似)
最坏: (n+1)/2(单支树)
左、右子树是平衡二叉树;
所有结点的左、右子树深度之差的绝对值≤ 1
平衡因子:该结点左子树与右子树的高度差
任一结点的平衡因子只能取:-1、0 或 1;如果树中任意一个结点的平衡因子的绝对值大于1,则这棵二叉树就失去平衡,不再是AVL树;
对于一棵有n个结点的AVL树,其高度保持在O(log2n)数量级,ASL也保持在O(log2n)量级。
如果在一棵AVL树中插入一个新结点,就有可能造成失衡,此时必须重新调整树的结构,使之恢复平衡。我们称调整平衡过程为平衡旋转。

基本思想:记录的存储位置与关键字之间存在对应关系,Loc(i)=H(keyi) 
优点:查找速度极快O(1),查找效率与元素个数n无关
哈希方法(杂凑法)
选取某个函数,依该函数按关键字计算元素的存储位置,并按此存放;
查找时,由同一个函数对给定值k计算地址,将k与地址单元中元素关键码进行比,确定查找是否成功。
哈希函数(杂凑函数):哈希方法中使用的转换函数
冲 突:不同的关键码映射到同一个哈希地址 key1?key2,但H(key1)=H(key2)
同义词:具有相同函数值的两个关键字
Hash(key) = a·key + b (a、b为常数)
优点:以关键码key的某个线性函数值为哈希地址,不会产生冲突。
缺点:要占用连续地址空间,空间效率低。
Hash(key)=key mod p (p是一个整数)
关键:如何选取合适的p?
技巧:设表长为m,取p≤m且为质数
1.开放定址法(开地址法) 2.链地址法
基本思想:有冲突时就去寻找下一个空的哈希地址,只要哈希表足够大,空的哈希地址总能找到,并将数据元素存入。 
Hi=(Hash(key)+di) mod m ( 1≤i < m )
其中:m为哈希表长度
di 为增量序列 1,2,…m-1,且di=i
优点:只要哈希表未被填满,保证能找到一个空地址单元存放有冲突的元素。
缺点:可能使第i个哈希地址的同义词存入第i+1个地址,这样本应存入第i+1个哈希地址的元素变成了第i+2个哈希地址的同义词,……,产生“聚集”现象,降低查找效率。
Hi=(Hash(key)+di) mod m ( 1≤i < m )
其中:m为哈希表长度
di 为随机数
基本思想:相同哈希地址的记录链成一单链表,m个哈希地址就设m个单链表,然后用用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构
step1 取数据元素的关键字key,计算其哈希函数值(地址)。若该地址对应的链表为空,则将该元素插入此链表;否则执行step2解决冲突。
step2 根据选择的冲突处理方法,计算关键字key的下一个存储地址。若该地址对应的链表为不为空,则利用链表的前插法或后插法将该元素插入此链表。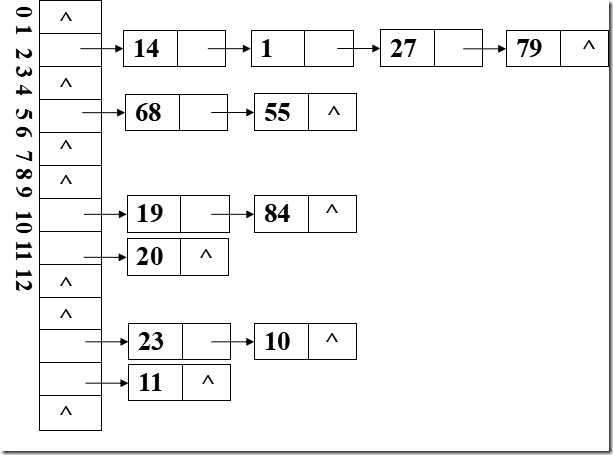
链地址法的优点:
非同义词不会冲突,无“聚集”现象
链表上结点空间动态申请,更适合于表长不确定的情况
标签:width oca type 不用 概率 元素 链式 数字分析 没有
原文地址:https://www.cnblogs.com/mohuishou-love/p/10400511.html