标签:present sharp ems push define where data empty rom
Input
Output
Sample Input
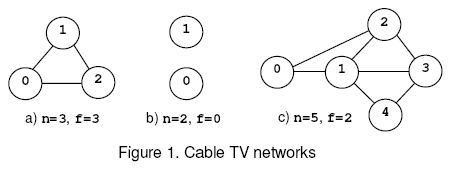
0 0 1 0 3 3 (0,1) (0,2) (1,2) 2 0 5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)
Sample Output
0 1 3 0 2
idea:
At first,这道题和最小割十分相似,可是我们要将割点转换为割边,将一个点拆成入点和出点
然后将入点向出点连一条边权为1的边,表示这个点删掉的代价为1,每一条无向边(a,b)需要将a的出点连向b的入点,反之亦然
这样删掉点就相当于删掉a的入点到a的出点这一条边,完成了点边转化
每一次,我们需要枚举源点和汇点,取最小值,源点要求是一个出点,汇点是一个入点,求最小割即保留源点和汇点的情况下使原图断开的最大花费
输出答案即可,上代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define MAXN 30002
using namespace std;
queue<int> Q;
int vals[MAXN],tot,t,n,m,ii,ij,to[MAXN],nxt[MAXN],val[MAXN],fir[MAXN],cur[MAXN],dep[MAXN];
void read(){
char ch=getchar();
while(ch!=‘(‘) ch=getchar();
ch=getchar(); ii=0;
while(‘0‘<=ch && ch<=‘9‘) ii=(ii<<1)+(ii<<3)+ch-‘0‘,ch=getchar();
ch=getchar(); ij=0;
while(‘0‘<=ch && ch<=‘9‘) ij=(ij<<1)+(ij<<3)+ch-‘0‘,ch=getchar();
}
void ade(int u,int v,int z){
//cout<<u<<" "<<v<<" "<<z<<endl;
val[++tot]=z;
to[tot]=v;
nxt[tot]=fir[u];
fir[u]=tot;
}
bool bfs(int s,int t){
memset(dep,0,sizeof(dep));
dep[s]=1; while(!Q.empty()) Q.pop();
Q.push(s);
while(!Q.empty()){
int x=Q.front(); Q.pop();
for(int k=fir[x];k!=-1;k=nxt[k]){
if(val[k] && !dep[to[k]]){
dep[to[k]]=dep[x]+1;
Q.push(to[k]);
}
}
}
if(dep[t]) return 1;
return 0;
}
int dfs(int x,int dis,int t){
if(x==t) return dis;
for(int k=cur[x];k!=-1;k=nxt[k]){
cur[x]=k;
if(dep[to[k]]==dep[x]+1 && val[k]){
int z=dfs(to[k],min(dis,val[k]),t);
if(z){
val[k]-=z; val[k^1]+=z;
return z;
}
}
}
return 0;
}
int Dinic(int s,int t){
int res=0,d;
while(bfs(s,t)){
rep(i,0,n*2-1) cur[i]=fir[i];
d=dfs(s,99999999,t);
while(d){
res+=d;
d=dfs(s,99999999,t);
}
}
return res;
}
int main(){
while(~scanf("%d%d",&n,&m)){
memset(fir,-1,sizeof(fir)); tot=-1;
rep(i,1,m){
read();
if(ii==ij) continue;
ade(ii+n,ij,99999999); ade(ij,ii+n,0);
ade(ij+n,ii,99999999); ade(ii,ij+n,0);
}
rep(u,0,n-1) ade(u,u+n,1),ade(u+n,u,0);
if(n==0 || m<n-1){
puts("0");
continue;
}
if(n==1){
puts("1");
continue;
}
rep(i,0,tot) vals[i]=val[i];
int ans=99999999;
rep(i,n,n+n-2){
rep(j,i+1,n+n-1)
{
rep(k,0,tot) val[k]=vals[k];
ans=min(ans,Dinic(i,j-n));
}
}
if(ans==99999999) ans=n;
printf("%d\n",ans);
}
return 0;
}
标签:present sharp ems push define where data empty rom
原文地址:https://www.cnblogs.com/handsome-zlk/p/10436555.html