标签:节点 math demo alt delete parent return node 删除节点
1 package Demo; 2 3 public class AVLtree { 4 private Node root; //首先定义根节点 5 6 private static class Node{ //定义Node指针参数 7 private int key; //节点 8 private int balance; //平衡值 9 private int height; //树的高度 10 private Node left; //左节点 11 private Node right; //右节点 12 private Node parent; //父母节点 13 14 15 Node(int key, Node parent){ //构造器中引用该构造器正在初始化的对象 16 this.key = key; 17 this.parent = parent; 18 19 } 20 } 21 public boolean insert(int key){ //判断这里是否能插入新的节点 22 if(root == null){ 23 root = new Node(key,null); 24 return true; 25 } 26 27 Node n = root; 28 while (true){ //如果根节点下的子节点和新插进来的子节点相同 29 if(n.key == key) 30 return false; //则不进行插入操作 31 32 Node parent = n; 33 34 boolean goLeft = n.key > key; //判断新的节点插入父母节点的左边or右边 35 n = goLeft ? n.left : n.right; //小的话插左边,大的话插右边 36 37 if(n == null){ 38 if(goLeft){ 39 parent.left = new Node (key,parent); 40 }else{ 41 parent.right = new Node(key,parent); 42 } 43 rebalance(parent); 44 break; 45 } 46 } 47 return true; 48 } 49 50 private void delete(Node node){ //删除节点 51 if(node.left == null && node.right == null){ 52 if(node.parent == null){ 53 root = null; 54 }else{ 55 Node parent = node.parent; 56 if(parent.left == node){ //如果父母节点的左孩子节点和根节点一样 57 parent.left = null; //则左节点为空 58 }else{ 59 parent.right = null; //反之右节点为空 60 } 61 rebalance(parent); 62 } 63 return ; 64 } 65 66 if(node.left != null){ //如果左节点不空 67 Node child = node.left; 68 while(child.right != null)child = child.right; 69 node.key = child.key; 70 delete(child); 71 }else{ 72 Node child = node.right; 73 while (child.left != null)child = child.left; 74 node.key = child.key; 75 delete(child); 76 } 77 } 78 79 public void Delete(int delKey){ 80 if(root == null) 81 return; 82 83 Node child = root; 84 while (child != null){ 85 Node node = child; //交换根节点给node , 再判断新的孩子节点插在哪里 86 child = delKey >= node.key ? node.right : node.left; 87 if(delKey == node.key){ 88 delete(node); 89 return; 90 } 91 } 92 } 93 94 private void setBalance(Node... nodes){ 95 for(Node n : nodes){ 96 reheight(n); 97 n.balance = height(n.right) - height(n.left); //平衡因子,任意节点左右子树高度差 98 } 99 } 100 101 private void rebalance (Node n){ 102 setBalance(n); 103 104 if(n.balance == -2){ 105 if(height(n.left.left) >= height(n.left.right)) 106 n = rotateRight(n); 107 else 108 n = rotateLeftThenRight(n) ; 109 110 }else if(n.balance == 2){ //等于2和-2都是不平衡的,需要重新调整 111 if(height(n.right.right) >= height(n.right.left)) 112 n = rotateLeft(n); 113 else 114 n = rotateRightThenLeft(n); 115 116 } 117 118 if(n.parent != null){ 119 rebalance(n.parent); 120 }else{ 121 root = n; 122 } 123 } 124 125 private Node rotateLeft(Node a){ 126 127 Node b = a.right; 128 b.parent = a.parent; 129 130 a.right = b.left; 131 132 if(a.right != null) 133 a.right.parent = a; 134 135 b.left = a; 136 a.parent = b; 137 138 if(b.parent != null){ 139 if(b.parent.right == a){ 140 b.parent.right = b; 141 }else{ 142 b.parent.left = b; 143 } 144 } 145 146 setBalance(a, b); 147 148 return b; 149 } 150 151 private Node rotateRight(Node a){ 152 153 Node b = a.left; 154 b.parent = a.parent; 155 156 a.left = b.right; 157 158 if(a.left != null){ 159 a.left.parent = a; 160 161 b.right = a; 162 a.parent = b; 163 164 if(b.parent.right == a){ 165 b.parent.right = b; 166 }else{ 167 b.parent.left = b; 168 } 169 } 170 171 setBalance(a, b); 172 173 return b; 174 } 175 176 private Node rotateLeftThenRight(Node n){ 177 n.left = rotateLeft(n.left); 178 return rotateRight(n); 179 } 180 181 private Node rotateRightThenLeft(Node n){ 182 n.right = rotateRight(n.right); 183 return rotateLeft(n); 184 } 185 186 private int height (Node n){ 187 if(n == null) 188 return -1; 189 return n.height; 190 } 191 192 193 194 public void printBalance(){ 195 printBalance(root); 196 } 197 198 private void printBalance(Node n){ 199 if(n != null){ 200 printBalance(n.left); 201 System.out.printf("%s ",n.balance); 202 printBalance(n.right); 203 } 204 } 205 206 private void reheight(Node node){ 207 if(node != null){ 208 node.height = 1 + Math.max(height(node.left),height(node.right)); //新的二叉平衡树高度为: 209 } 210 } 211 public static void main(String[] args) { 212 AVLtree tree = new AVLtree(); 213 214 System.out.println("Inserting values 1 to 10"); //最后输出的结果代表平衡因子,0为左右子树高度相等,1为左右子树高度相差1层 215 for (int i = 1; i < 10; i++) 216 tree.insert(i); 217 218 System.out.println("Print balance : "); 219 tree.printBalance(); 220 } 221 }
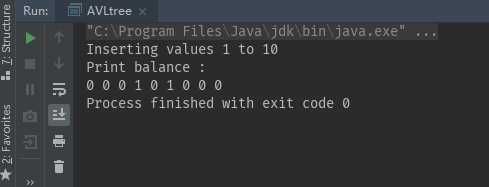 可以动手画一下生成的AVL树,亲测算法符合结果。
可以动手画一下生成的AVL树,亲测算法符合结果。
java项目---用java实现二叉平衡树(AVL树)并打印结果(详)
标签:节点 math demo alt delete parent return node 删除节点
原文地址:https://www.cnblogs.com/kkuuklay/p/10462193.html