标签:str 了解 代码 %s 自己 int 复杂度 解决 相等
KMP是啥?KMP当然是KMPlayer的简称啦
KMP算法是用来解决字符串匹配的一种算法,由D.E.Knuth、J.H.Morris和V.R.Pratt同时发现,然后它可以用来干啥呢?我们上个例题:
给定两个字符串\(S,T\),问\(T\)在\(S\)中出现了多少次,出现的起始位置不同即为不同
\(O(n^2)\)暴力!(我当然知道你会)
\(|S|,|T|\leqslant 10^5\),怎么做?
所以我们这时我们就需要引入KMP算法,它能在最坏\(O(n)\)的复杂度下解决子串匹配的问题
首先我们考虑一下\(O(n^2)\)的冗余在哪里?举个栗子吧,我令S=‘aaaaaaaaac‘,T=‘aaaac‘,然后跑一遍\(O(n^2)\),你会发现每次\(S_{i+5}\)与\(T_5\)失配后,它会从\(S_{i+1}\)从头开始匹配,但是,其实没必要重新开始对吧?因此你发现这个\(O(n^2)\)的算法做了非常多没有意义的匹配,导致时间复杂度急剧增加,然后就TLE了
发现问题自然需要解决,如何解决?KMP算法就基于这个冗余提出了优化方案,它建立了一个对于任意字符串\(S\)而言的Next(C++11中next是关键字,所以我使用大写,并在之后简称为\(N\)数组)数组,\(N_i\)表示\([S_1...S_i]\)中前缀后缀相等的长度,也就是有\([S_1...S_{N_i}]=[S_{i-N_i+1}..S_i]\),举个栗子,若字符串S=‘abcabc‘,则它的\(N\)数组为\(\{0,0,0,1,2,3\}\)(\(N_1=0\)是定义的)
有了\(N\)数组后有何用?既然是为了解决冗余的,那我们就来看看它如何解决这个冗余。我们依然采用之前的栗子,首先对于\(T\)串求出其\(N\)数组:\(\{0,1,2,3,0\}\),然后我们进行匹配,然后遇到\(S_5\)与\(T_5\)失配,然后怎么处理?
当然把它俩从头开始啊(\(n^2\)了啊喂,你\(N\)白求了);你发现\(T_4\rightarrow T_5\)过程中与\(S_4\rightarrow S_5\)失配了,然后想想\(N\)数组的性质,可能存在\(T_{N_4}\rightarrow T_{N_4+1}\)能匹配啊,然后你就只需要把枚举\(T\)的指针疯狂跳\(N\)数组,直到能匹配为止
然后我们画个图来理解一下
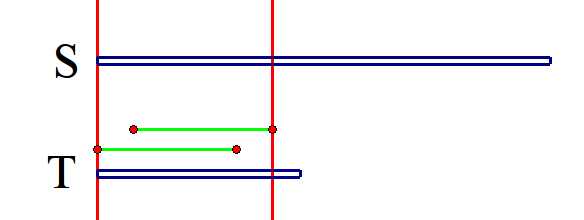
这里红色平行线之间的完全相同的部分,之后就是失配的字符,绿色的便是后缀和前缀相同的部分
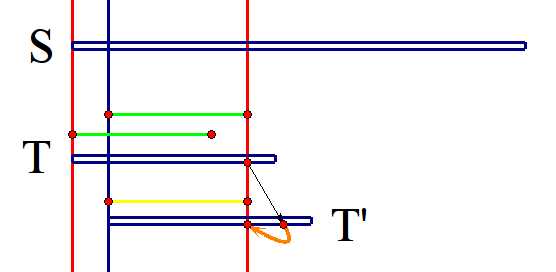
然后我们就将T往后挪一点点,黄色部分和绿色部分相同,然后黑色箭头则说明T中的位置在T‘中对应的位置,棕色箭头即为跳\(N\)数组的过程
然后我们贴个代码
for (int i=1,j=0;i<=Lens;i++){
while (j&&s[i]!=t[j+1]) j=Next[j];
if (s[i]==t[j+1]) j++;
if (j==Lent) j=Next[j],Ans++;//就算匹配了也要跳一次匹配其他的,因为是统计出现次数
}然后这题就做完了对吧?不对,我还没有讲\(N\)数组的构造方法……其实构造方法和匹配差不多,贴个代码,读者们可以自己看下
for (int i=2,j=0;i<=Lent;i++){
while (j&&t[i]!=t[j+1]) j=Next[j];
if (t[i]==t[j+1]) j++;
Next[i]=j;
}然后我们来考虑一下时间复杂度,显然是\(O(n)\)的,做道例题吧
求\(T\)在\(S\)中的出现位置,并且输出\(T\)的Next数组
直接套用板子就好
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x>=10) print(x/10);
putchar(x%10+'0');
}
const int N=1e6;
char t[N+10],s[N+10];
int Next[N+10];
int Lens,Lent,ans;
void get(){
for (int i=2,j=0;i<=Lent;i++){
while (j&&t[i]!=t[j+1]) j=Next[j];
if (t[i]==t[j+1]) j++;
Next[i]=j;
}
}
void work(){
get();
for (int i=1,j=0;i<=Lens;i++){
while (j&&s[i]!=t[j+1]) j=Next[j];
if (s[i]==t[j+1]) j++;
if (j==Lent) j=Next[j],printf("%d\n",i-Lent+1);
}
}
int main(){
scanf("%s",s+1);
scanf("%s",t+1);
Lens=strlen(s+1),Lent=strlen(t+1),ans=0;
work();
for (int i=1;i<=Lent;i++) i!=Lent?printf("%d ",Next[i]):printf("%d\n",Next[i]);
return 0;
}标签:str 了解 代码 %s 自己 int 复杂度 解决 相等
原文地址:https://www.cnblogs.com/Wolfycz/p/10482481.html