标签:svm set sla 这一 port 优化问题 col 就是 等价
学SVM看到对偶问题的时候很难受,因为看不懂,数学知识真的太重要了。后来在B站看到某up主的精彩推导,故总结如下。
由之前最大化间隔的计算可得SVM的基本型为:
$\underset{\mathbf{w},b}{min}\ \ \ \ \frac{1}{2}\left \| \mathbf{w}\right \|^{2}$
$s.t. \ y_{i}(\mathbf{w}^{T}\mathbf{x}_{i})+b\geqslant 1,\ \ \ \ i=1,2,\cdots ,m.$
现在将上式转化为其对偶问题,通过求解对偶问题来得到原始问题的解。
根据拉格朗日乘子法,对上式的每条约束添加拉格朗日乘子$\lambda _{i} \geqslant 0$,于是该问题的拉格朗日函数可写为:
$L(\mathbf{w},b,\lambda ) = \frac{1}{2}\left \| \mathbf{w} \right \|^{2}+\sum_{i=1}^{m}\lambda _{i}(1-y_{i}(\mathbf{w}^{T}\mathbf{x}_{i}+b))$ $\mathbf{\lambda }=(\lambda _{1};\lambda _{2};\cdots ;\lambda _{m})$
由此得到了重要的第一步,将带约束的原问题转化为了无约束的原问题,即:
$\underset{\mathbf{w},b}{min}\ \ \ \ \frac{1}{2}\left \| \mathbf{w}\right \|^{2}$ -------------------> $ \underset{\mathbf{w},b}{min}\ \underset{\mathbf{\lambda }}{max}\ L(\mathbf{w},b,\mathbf{\lambda})$
$s.t. \ y_{i}(\mathbf{w}^{T}\mathbf{x}_{i})+b\geqslant 1,\ \ \ \ i=1,2,\cdots ,m.$ -------------------> $s.t.\ \ \lambda _{i}\geqslant 0$
为什么这两种是等价的呢?从逻辑上可以简单分析:

接下来第二步转化就是将无约束的原问题转化为对偶问题,即:
$ \underset{\mathbf{w},b}{min}\ \underset{\mathbf{\lambda }}{max}\ L(\mathbf{w},b,\mathbf{\lambda})$ -------------------> $ \underset{\mathbf{\lambda }}{max}\ \underset{\mathbf{w},b}{min}\ L(\mathbf{w},b,\mathbf{\lambda})$
$s.t.\ \ \lambda _{i}\geqslant 0$ -------------------> $s.t.\ \ \lambda _{i}\geqslant 0$
在二次凸优化的条件下,这两者就是强对偶关系,是等价的。
综上,这一系列的步骤就是SVM基本型(带约束的原问题)——>不带约束的原问题——>对偶问题。
对于这个对偶问题,我们首先固定$\lambda$,求解$w,b$,由于$w,b$不受约束,所以这是无约束的优化问题,直接求导即可。这里需要说明的一点就是因为这是凸函数,二阶导数必然大于0,所以令偏导为零的点就是最小值点。计算过程如下所示:
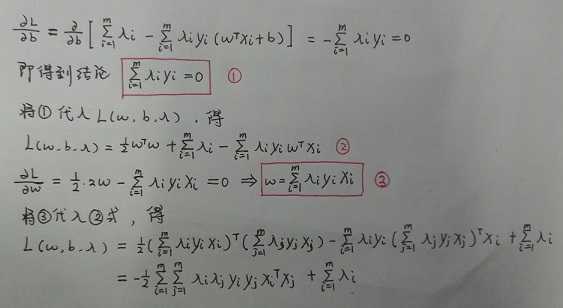
消去$\mathbf{w},b$后得到对偶问题:
$\underset{\mathbf{\lambda }}{max}\ \ \sum_{i=1}^{m} \lambda _{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda _{i}\lambda _{j}y_{i}y_{j}\mathbf{x}_{i}^{T}\mathbf{x}_{j}$
$s.t.\ \ \lambda _{i}\geqslant 0$
支持向量机(Support Vector Machine):对偶
标签:svm set sla 这一 port 优化问题 col 就是 等价
原文地址:https://www.cnblogs.com/zyb993963526/p/10486608.html