标签:操作 集合 起点 自己 形式 字符串 bsp 函数 最小化
这个项目是笔者在修的课程《编译原理》的实验。实验要求如下:
实验内容:
设计一个应用软件,以实现将正则表达式-->NFA--->DFA-->DFA最小化-->词法分析程序
实验要求:
(1)要提供一个源程序编辑界面,让用户输入正则表达式(可保存、打开源程序)
(2)需要提供窗口以便用户可以查看转换得到的NFA(用状态转换表呈现即可)
(3)需要提供窗口以便用户可以查看转换得到的DFA(用状态转换表呈现即可)
(4)需要提供窗口以便用户可以查看转换得到的最小化DFA(用状态转换表呈现即可)
(5)需要提供窗口以便用户可以查看转换得到的词法分析程序(该分析程序需要用C语言描述)
(6)应该书写完善的软件文档
说明:
本来作为一个课程实验项目似乎没什么可讲的,但是笔者觉得这个项目要求非(sang)常(xin)睿(bing)智(kuang),这其间所用到的一些解决方法可能会对大家有所帮助,于是在此分享。
项目及详细说明已经上传到GitHub上了,有兴趣可以看看:
https://github.com/sureyet/SCNU-CompilerLab2
正文:
说明:本实验实现的编程语言为C++,实验环境Qt5.9.2
一、 界面介绍
本程序的界面如图所示。
使用说明:
1. 在程序的左上方提供了一个输入框供用户自行输入正则表达式或者点击打开文件按钮选择文件(注意文件路径不能带有中文且文件必须是txt),要注意的是输入的正则表达式不能带字符‘e’,这是因为在生成nfa时,我用字符‘e’替代了epsilon。另外本程序也可保存在输入框里的正则表达式,保存的路径为本程序的运行路径,文件名为re.txt。
2.在用户确认输入完正则表达式后,按下“开始分析”键开始分析。
3.按下“开始分析”键后,用户便可以通过按下“展示NFA”,“展示DFA”,“最小化DFA”,“生成分析程序”查看转化结果。值得一提的是,本程序用图的形式将NFA、DFA以及最小化DFA展示出来,这算是本程序的亮点所在。
一、 设计思路:
本程序通过5个阶段地处理,将用户输入的正则表达式一步步转化,直到最终生成分析程序代码(用C语言描述),这5个阶段分别是:将正则表达式转化为后缀表达式、将后缀表达式转化为NFA、将NFA转化为DFA、DFA的最小化、生成生成词法分析程序。
以下是这5个阶段的详细说明:
A)第一阶段:当在程序的输入框里键入正则表达式,按下“开始转化”按钮,程序会先在获取到的正则表达式字符串里插入连接符“.”,接着调用函数将其转化为后缀表达式,方便后续处理。
B) 第二阶段:程序将逐字符读取该后缀表达式,判断该字符的类型(普通字符还是操作符:选择、连接、闭包),并调用对应的函数去处理,最终生成一张NFA图。
C) 第三阶段:这部分用到的算法是“子集构造法”,先取出NFA的初始结点,调用函数将将该结点能通过epsilon达到的结点聚集起来形成一个集合,作为DFA的初始结点,接着分别用原来正则表达式的字符去构造新的集合,每构造一个新的集合,DFA就多了一个结点,该结点与原结点的边的值就是用来构造的那个正则表达式字符。接着对新的结点重复以上过程,直到没有新的结点生成,此时DFA的构造也就结束了。
给一个例子:
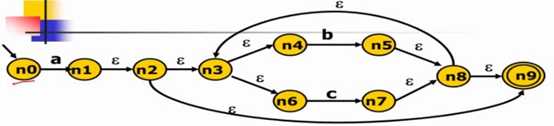
这个算法的正则表达式是a(b|c)*。
对于 ε 的边表示一种零代价的转换,n1 可以在没有任何输入操作的情况下直接滑动到 n2,也就是 n1 和 n2 是等价的。
所以 n0 通过 a 可以走到 n1, n2, n3, n4, n6, n9。我们可以将这样的 6 个元素记为一个集合 q1。 q1 = {n1, n2, n3, n4, n6, n9} 。
q1 通过 b 可以得到:n5, n8, n9, n3, n4, n6 ,记为 q2。
q2 继续通过某一节点得到 q3,继续重复该步骤,得到所有的子集。
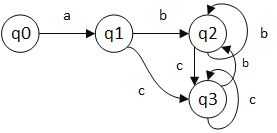
所以 q0 通过 a 得到 q1, q1 通过 b 得到 q2 .... ,最终可以将 NFA 转化为一个 DFA。
因为 q1 和 q2 中都包含 n9, 所以 q1 和 q2 都是接受状态。
对于子集的求解,首先我们先看出在 NFA 中的下一状态,如 q1 的下一状态记为 delta(q1), 在这里是 {n5} 。之后求它的边界, 即每一个元素都通过 ε 走到能走到的所有状态,记为 q1 的闭包。
D) 第四阶段:这部分用到的算法是“Hopcroft 算法”,最小化DFA的过程和生成DFA的过程有些许类似。首先将DFA结点分为两类:一类是终结符集,另一类是非终结符集 ,将这两个集合加入队列,取出一个集合,判断这个集合能否再分割,如果不能,则生成一个新的最先DFA图结点,如果可以,则分割成若干的新的子集加入队列,从队列中取出新的集合,重复以上过程直到队列为空。
这里也给一个例子:
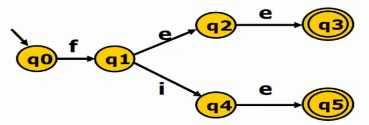
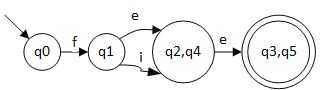
这个算法的正则表达式是 fee 或者 fie,可以通过 fee 或 fie 到达终结状态
N : {q0, q1, q2, q4}
A : {q3, q5}
在 N 中 q0 和 q1 在接受 e 的条件下最终得到的状态还是在 N 的内部。所以可以将其根据 e 拆分成 {q0, q1}, {q2, q4}, {q3, q5}
对于 q2 和 q4 都可以接受 e ,而且最终达到的状态一致,所以不能再进行切分。
q0 和 q1 ,在接受 e 的时候, q0 最终得到还是在 {q0, q1}这个状态的结合中, q1 却会落在 {q2, q4} 的状态中,所以可以将 q0 和 q1 分为 {q0}, {q1}。
E) 第五阶段:生成词法分析程序(用C语言描述),从最小化DFA图的起点开始遍历即可,DFA的初态(即起点)一定是唯一的,而接收态(即终点结点)可能有多个(如正则表达式”a|b”)。进行遍历,如果边指向自己则是while语句,先翻译while语句,然后对于每条前进边都是if-else语句,如果不是第一条if-else语句,则需在开头加上else,实现else if 的衔接。
补充:本程序中NFA、DFA、最小化DFA的存储结构用的是图(邻接表)结构。
一、 核心代码
a) 将正则表达式插入连接符“.”并转化成后缀表达式。
这里转化为后缀表达式我是借鉴了《数据结构》里四则表达式转化为后缀表达式的方法。


b) 将后缀表达式转化为NFA
设计思路已在前面提到,基本过程是逐字符读取后缀表达式,判断字符的类型,再调用对应的函数处理。主控代码如下:

这里说明一下一个细节:如何记录上一步操作的NFA结点在邻接表中的序号,答案是用一个栈。
举个例子:正则表达式(a|b)*的后缀表达式为ab|*,接着生成NFA图。
开始遍历,第一个字符是‘a’,判断是普通字符,往NFA图的邻接表中插入两结点(0,1),用一条边连接起来,边的值为a。往栈里push进0和1。
第二个字符是‘b’,一样操作后,往栈里push进2和3。利用栈后进先出的特性,就能记录上一步操作的NFA结点在邻接表中的序号。
接着一个字符是‘|’,判断为操作符。调用对应函数处理:

最后往栈里push进新生成的结点的序号,下一步操作只需要处理这一步操作生成的新结点就行。
最后一个字符是‘*’,调用对应的函数:

处理到这里就结束了,值得注意的是,闭包最后的操作也是往栈里面push进新生成结点的序号,由于处理到这里就结束了,因此栈里最底层的序号,就是NFA图的起始结点在邻接表里的序号。
标签:操作 集合 起点 自己 形式 字符串 bsp 函数 最小化
原文地址:https://www.cnblogs.com/sureyet/p/10500926.html