标签:for span 路径 body mamicode ret -- name 代码
思路:一个S集合存已经遍历的顶点,一个Q集合存未遍历的顶点。一个dist列表存从初始点到当前点的最短路径,即dist[i] 表示初始点到i所需的最短距离。
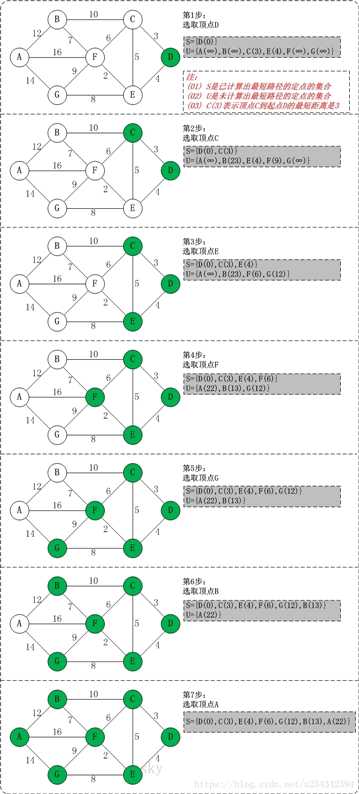
伪代码:

代码:
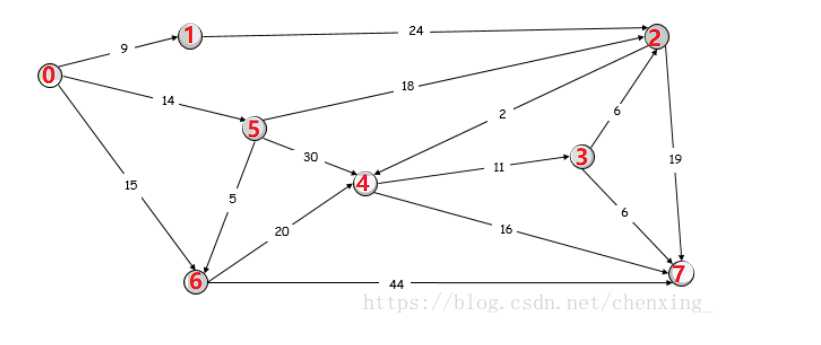
MAX_value = 999999 def dijkstra(graph, s): dist = [MAX_value] * len(graph) dist[s] = 0 S = [] Q = [i for i in range(len(graph))] while Q: u_dist = min([d for i,d in enumerate(dist) if i in Q]) u = dist.index(u_dist) S.append(u) Q.remove(u) for v , d in enumerate(graph[u]): if 0 < d < MAX_value: dist[v] = min(dist[v] , dist[u] + d) return dist if __name__ == ‘__main__‘: graph_list = [[0, 9, MAX_value, MAX_value, MAX_value, 14, 15, MAX_value], [9, 0, 24, MAX_value, MAX_value, MAX_value, MAX_value, MAX_value], [MAX_value, 24, 0, 6, 2, 18, MAX_value, 19], [MAX_value, MAX_value, 6, 0, 11, MAX_value, MAX_value, 6], [MAX_value, MAX_value, 2, 11, 0, 30, 20, 16], [14, MAX_value, 18, MAX_value, 30, 0, 5, MAX_value], [15, MAX_value, MAX_value, MAX_value, 20, 5, 0, 44], [MAX_value, MAX_value, 19, 6, 16, MAX_value, 44, 0]] distance = dijkstra(graph_list, 0) print(distance)
|
 |
标签:for span 路径 body mamicode ret -- name 代码
原文地址:https://www.cnblogs.com/Lee-yl/p/10503983.html