标签:auto ext 功能实现 [] 实现 组成 数组遍历 设计 print
1.输入一个整形数组,数组里面有正数也有负数。
2.数组中国连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
3.求所有子数组的和的最大值。要求时间复杂度为O(n)。
当自己看到这个题目的时候,想到了“复杂的问题简单化,一步一步来”,然后在课上老师的引导之下有了自己实现这个功能的方法。最终自己用了两者方法实现功能,但是在第二种方法上花费的时间较多,几乎是第一种方法两倍的时间。下面将两种方法一一解释自己的思路。
一、时间复杂度O(n^2)
本次功能实现简单,一共分为3步,首先是实现数组的输入,然后进行一个或多个连续子数组的求和,最后进行比较。但需要注意的是,求和以及比较是同时存在的。
本次实现功能的过程中遇到了一个小小的问题,就是将自己用来记录最大值的变量f赋初值为0,忽略了数组中的值全为负数时的情况,最终解决将f赋初值为数组中第一个数,解决了问题。
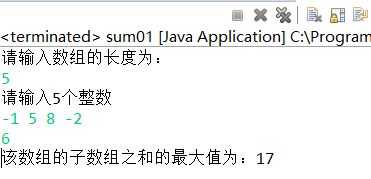
以下是完整代码以及测试结果:
import java.util.Scanner; public class sum01 { public static void main(String[] args) { // TODO Auto-generated method stub //整形数组的输入 Scanner sc = new Scanner(System.in); System.out.println("请输入数组的长度为:"); int n=sc.nextInt(); int[] c = new int[n]; System.out.println("请输入"+n+"个整数"); for(int i=0;i<n;i++) { c[i] = sc.nextInt(); } //子数组求和以及大小比较 int f=c[0];//定义整形变量f,为子数组最大值 int sum=0;//定义整形变量sum,为子数组求和 for (int j=0;j<n;j++) { for (int i=j;i<n;i++) { sum=sum+c[i]; if(f<sum) { f=sum;//每次求和之后将sum与已有的最大值进行比较 } } sum=0; } System.out.println("该数组的子数组之和的最大值为:"+f); }
二、时间复杂度O(n)
第二种方案就是实现要求中时间复杂度为O(n)的问题,该程序的设计思想是,从数组中第一个值开始进行加法运算,如果sum值加到某数为负(包括数组中所有整数为负的情况),则将sum值归0(因为数组的子数组为连续,所以sum值可以直接归0),如果sum值大于已有的最大值f,那么给f赋新值sum,如此循环直至数组遍历一遍,最终如果sum不为零,则计算结果就是最大整数,若sum值为0,才需二次遍历数组寻找数组中的最大值。
以下是完整代码以及测试结果:
import java.util.Scanner; public class sum02 { public static void main(String[] args) { // TODO Auto-generated method stub Scanner sc = new Scanner(System.in); System.out.println("请输入数组的长度为:"); int n=sc.nextInt(); int[] c = new int[n]; System.out.println("请输入"+n+"个整数"); for(int i=0;i<n;i++) { c[i] = sc.nextInt(); } int f=0;//定义整形变量f,为子数组最大值 int sum=0;//定义整形变量sum,为子数组求和 for(int i=0;i<n;i++) { sum = sum+c[i]; if(sum < 0) { sum=0; } if(sum > f) { f = sum; } } if(sum == 0) { for(int i=0;i<n;i++) { if(i == 0) { f = c[i]; } if(f < c[i]) { f = c[i]; } } } System.out.println("该数组的子数组之和的最大值为:"+f); } }

此外,在课上还有许多同学提出了自己的观点,首先将数组的最大值找出,然后在围绕最大值进行求和运算的方法也是可行的,但自己还没有用代码进行实现,但同学的设计思路自己已经明白了。
一问多解,像极了自己以前热爱的数学问题,生活中许多问题也是这样,真神奇!
标签:auto ext 功能实现 [] 实现 组成 数组遍历 设计 print
原文地址:https://www.cnblogs.com/Qi77/p/10505647.html