标签:style 例子 初始 turn 解决问题 简介 调用 结果 状态
一、斐波那契数列(递归VS动态规划)

1、斐波那契数列——递归实现(python语言)——自顶向下
递归调用是非常耗费内存的,程序虽然简洁可是算法复杂度为O(2^n),当n很大时,程序运行很慢,甚至内存爆满。
1 def fib(n): 2 #终止条件,也就是递归出口 3 if n == 0 or n == 1: 4 return 1 5 else: 6 #递归条件 7 return (fib(n-1) + fib(n - 2))
2、斐波那契数列——动态规划实现(python语言)——自底向上
动态规划——将需要重复计算的问题保存起来,不需要下次重新计算。对于斐波那契数列,算法复杂度为O(n)。
1 def dp_fib(n): 2 #初始化一个数组,用于存储记录计算的结果。 3 res = [None] * (n + 1) 4 #前两项设置为1。 5 res[0] = res[1] = 1 6 #自底向上,将计算结果存入数组内。 7 for i in range(2, (n + 1)): 8 res[i] = res[i-1] + res[i-2] 9 return res[n]
3、方法概要
(1)构造一个公式,它表示一个问题的解是与它的子问题的解相关的公式:
![]()
(2)为这些子问题做索引,以便于它们能够在表中更好的存储与检索(用数组存储)。
(3)以自底向上的方法来填写这个表格;首先填写最小的子问题的解。
(4)这就保证了当我们解决一个特殊的子问题时,可以利用比它更小的所有可利用的子问题的解。
总之,因为在上世纪40年代(计算机普及很少时),这些规划设计是与“列表”方法相关的,因此被称为动态规划——Dynamic Programing。
二、动态规划算法——思想简介
1、DP算法思想
(1)将待求解的问题分解称若干个子问题,并存储子问题的解而避免计算重复的子问题,并由子问题的解得到原问题的解。
(2)动态规划算法通常用于求解具有某种最有性质的问题。
(3)动态规划算法的基本要素:最优子结构性质和重叠子问题。
最优子结构性质:问题的最优解包含着它的子问题的最优解。即不管前面的策略如何,此后的决策必须是基于当前状态(由上一次的决策产生)的最优决策。
重叠子问题:在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些问题被反复计算多次。对每个子问题只解一次,然后将其解保存起来,
以后再遇到同样的问题时就可以直接引用,不必重新求解。
2、DP算法——解决问题的基本特征
(1)动态规划一般求解最值(最优、最大、最小、最长)问题;
(2)动态规划解决 的问题一般是离散的,可以分解的(划分阶段的)。
(3)动态规划结局的问题必须包含最优子结构,即可以有(n-1)的最优推导出n的最优。
3、DP算法——解决问题的基本步骤
动态规划算法的四个步骤:
(1)刻画最优解的结构特性。(一维、二维、三维数组);
(2)递归的定义最优解。(状态转移方程)
(3)以自底向上的方法来计算最优解。
(4)从计算得到的解来构造一个最优解。
4、求解例子——求阶乘 n!

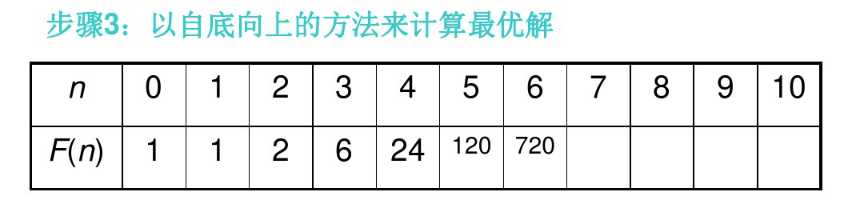
1 #递归实现求阶乘 2 def multiply(n): 3 if n == 0 or n == 1: 4 return 1 5 return n * multiply(n -1) 6 7 8 #动态规划实现求阶乘 9 def dp_multiply(n): 10 temp = [None] * (n + 1) 11 temp[0] = 1 12 temp[1] = 1 13 for i in range(2, n + 1): 14 temp[i] = i * temp[i - 1] 15 return temp[n]
动态规划——DP算法(Dynamic Programing)
标签:style 例子 初始 turn 解决问题 简介 调用 结果 状态
原文地址:https://www.cnblogs.com/xiaoboge/p/10509619.html