标签:补充 计算 解法 img ios using eal ble mes
凸包问题是算法中经典的题目了,最近算法课讲分治问题时提到了Convex Hull,算法导论的书上也花了篇幅讨论了Convex Hull的求解,主要是Graham方法。
为了能更好地理解分治和Graham这两种解法,我决定自己动手把代码写一遍。
然而,在写之前,我发现我大一学的用行列式求解由三个点围城的三角形面积已经忘得差不多了,现在补充一下:
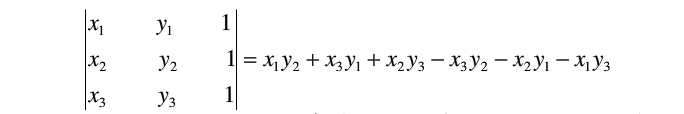
利用这个计算结果来判断点p3在p1p2直线的左侧还是右侧
下面是分治算法求解:
#include <iostream> #include <algorithm> #include <stdlib.h> #define N 100 using namespace std; int n=0; struct POINT { int x,y; }p[N],ans[N]; int visit[N],mark[N]; int Djudge(POINT a1,POINT a2,POINT a3) { int calculate=a1.x*a2.y+a3.x*a1.y-a3.x*a2.y-a2.x*a1.y-a1.x*a3.y; return calculate; } bool cmpxy(const POINT a,const POINT b) { if(a.x!=b.x) return a.x<b.x; else return a.y<b.y; } /*在涉及到平面上点对问题时,经常会按照这种方法对点进行排序 这与后面的sort(p,p+n,cmpxy)经常一起使用,在最近我做的2D maximal finding problem时,也是 使用了这样的排序对点对进行预处理。 */ void DealLeft(int first,int last) { int max=0,index=-1; int i=first; if(first<last) { for(i=first+1;i<last;i++) { int calcu=Djudge(p[first],p[i],p[last]); if(calcu==0) visit[i]=1; if(calcu>max) { max=calcu; index=i; } } } else { for(i-1;i>last;i--) { int calcu=Djudge(p[first],p[i],p[last]); if(calcu==0) visit[i]=1; if(calcu>max) { max=calcu; index=i; } } } if(index!=-1) { visit[index]=1; DealLeft(first,index); DealLeft(index,last); } } int main() { cout<<"Enter the number of the points: "; cin>>n; cout<<"Enter the points: "; for(int i=0;i<n;i++) { cin>>p[i].x>>p[i].y; visit[i]=0; } visit[0]=1; visit[n-1]=1; sort(p,p+n,cmpxy); DealLeft(0,n-1); DealLeft(n-1,0); int t=0; for(int i=0;i<n;i++) { if(visit[i]==1) { ans[t].x==p[i].x; ans[t].y==p[i].y; t++; } } //顺时针输出 mark[0]=mark[t-1]=1; for(int i=1;i<t-1;i++) mark[i]-0; cout<<ans[0].x<<" "<<ans[0].y<<endl; for(int i=1;i<t-1;i++) { int d=Djudge(ans[0],ans[t-1],ans[i]); if(d>=0) { cout<<ans[i].x<<" "<<ans[i].y<<endl; mark[i]=1; } } cout<<ans[t-1].x<<" "<<ans[t-1].y<<endl; for(int i=1;i<t;i++) { if(mark[i]!=1) { int d=Djudge(ans[0],ans[t-1],ans[i]); if(d<0) { cout<<ans[i].x<<" "<<ans[i].y<<endl; } } } return 0; }
标签:补充 计算 解法 img ios using eal ble mes
原文地址:https://www.cnblogs.com/CuteyThyme/p/10596679.html