标签:位置 printf 个数 超出 strong img 赋值 开始 info
讨论幻方前,先讨论一下动态申请数组大小
众所周知 在C语言中必须指定数组的大小 否则会报错。如果你不知道你要申请多大的数组怎么办?初始化一个非常大的数组?显然浪费空间。。
头文件#include<stdlib.h> 为我们提供了malloc函数 即动态内存分配函数 我们可以用它来为我们分配我们想要的数组大小
你想分配一个自己键盘输入大小的数组 就用malloc函数来实现(以下代码都用伪代码表示)
本题的申请数组就将用到这个方法
1.int *arr;//声明一个指针变量
scanf("%d",&n);
a=(int *)malloc(sizeof(int)*n);//这样就新建了一个长度为n的一维数组
2.int **arr;//声明一个二级指针 即指向指针的指针
scanf("%d",&n);
arr = (int **)malloc(sizeof(int*)*n);//申请一个n*n的二维数组
for (i = 0;i < n;i++)
arr[i] = (int *)malloc(sizeof(int)*n);
一、幻方按照阶数可分成了三类,即奇数阶幻方、双偶阶幻方(n%4==0)、单偶阶幻方(n-2%4==0)
奇数阶幻方(劳伯法)
奇数阶幻方最经典的填法是罗伯法。填写的方法是:
把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:
(1)每一个数放在前一个数的右上一格;
(2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;
(3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;
(4)如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在底行且最左列;
(5)如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:
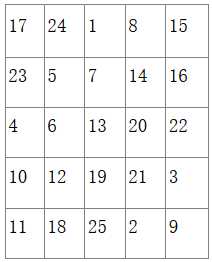
二、双偶数阶幻方(海尔法)
所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。在说解法之前我们先说明一个“互补数”定义:就是在n阶幻方中,如果两个数的和等于幻方中最大的数与1的和(即n×n+1),我们称它们为一对互补数。如在三阶幻方中,每一对和为10的数,是一对互补数 ;在四阶幻方中,每一对和为17的数,是一对互补数。
双偶数阶幻方最经典的填法是海尔法。填写的方法是:
以8阶幻方为例:
(1)先把数字按顺序填。然后,按4×4把它分割成4块(如图)
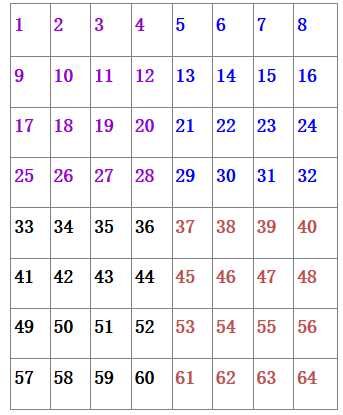
(2)每个小方阵对角线上的数字(如左上角小方阵部分),换成和它互补的数。
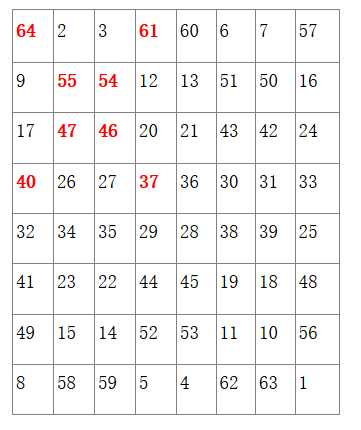
三、单偶数阶幻方(斯特拉兹法)
所谓单偶阶幻方就是当n不可以被4整除时的偶阶幻方,即4K+2阶幻方。如(n=6,10,14……)的幻方。
单偶数阶幻方最经典的填法是斯特拉兹法。填写的方法是:
以10阶幻方为例。这时,k=2。
(1)把魔方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数。

(2)在A象限的中间行、中间格开始,按自左向右的方向,标出k格。A象限的其它行则标出最左边的k格。将这些格,和C象限相对位置上的数互换位置。
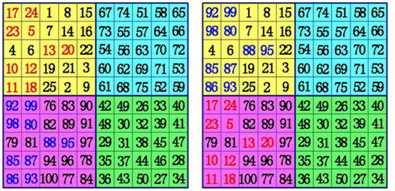
(3)在B象限所有行的中间格,自右向左,标出k-1格。(注:6阶幻方由于k-1=0,所以不用再作B、D象限的数据交换),将这些格,和D象限相对位置上的数互换位置。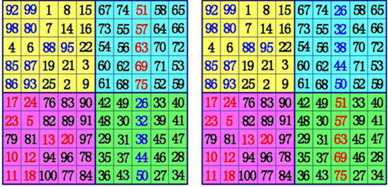
C语言代码如下(才疏学浅代码尽力了)
#include<stdio.h>
#include<stdlib.h>
int laobo(int n,int **arr,int num)
//劳伯法 用于计算奇数阶的情况
{
int i, j, k;
i = 0;
j = n / 2;
for (k = num;k <=num+n*n-1;k++)
//num代表第一个数 之所以引入这个num是因为后面有个函数需要
//一般来说 是以1开始
{
arr[i][j] = k;
if (arr[(i - 1 + n) % n][(j + 1 + n) % n] == 0)
{
i = (i - 1 + n) % n;
j = (j + 1 + n) % n;
}
else
{
i= (i + 1 + n) % n;
}
}
return 0;
}
int Init(int n, int **arr)
{
//初始化数组 形成 1 2 3 4
// 5 6 7 8.....这类
//为海尔法做好基础
int i, j, num;
num = 1;
for (i = 0;i < n;i++)
{
for (j = 0;j < n;j++)
{
arr[i][j] = num++;
}
}
return 0;
}
int haier(int n, int **arr)//被4整除时用该函数
{
int i, j, complement, deg;//complement表示互补数 即n*n+1
//deg表示n/4 因为要分成4*4的
complement = n*n + 1;
deg = n / 4;
for (i = 0;i < deg;i++)
{
for (j = 0;j < deg;j++)
{
arr[i * 4 + 0][j * 4 + 0] = complement - arr[i * 4 + 0][j * 4 + 0];
arr[i * 4 + 0][j * 4 + 3] = complement - arr[i * 4 + 0][j * 4 + 3];
arr[i * 4 + 1][j * 4 + 1] = complement - arr[i * 4 + 1][j * 4 + 1];
arr[i * 4 + 1][j * 4 + 2] = complement - arr[i * 4 + 1][j * 4 + 2];
arr[i * 4 + 2][j * 4 + 1] = complement - arr[i * 4 + 2][j * 4 + 1];
arr[i * 4 + 2][j * 4 + 2] = complement - arr[i * 4 + 2][j * 4 + 2];
arr[i * 4 + 3][j * 4 + 0] = complement - arr[i * 4 + 3][j * 4 + 0];
arr[i * 4 + 3][j * 4 + 3] = complement - arr[i * 4 + 3][j * 4 + 3];
}
}
return 0;
}
int late(int n, int **arr)
{
int deg;
int k;
int temp;
int i, j;
deg = n / 2;
//laobo(deg,n, arr, x, y, num);//用laobo法填充A象限
//laobo(deg,n, arr, x+deg, y+deg, num+deg*deg);//用laobo法填充D象限
//laobo(deg,n, arr, x+deg, y, num+2*deg*deg);//用laobo法填充B象限
//laobo(deg,n, arr, x, y+deg, num+3*deg*deg);//C
int **a;
a = (int **)malloc(sizeof(int*)*deg);
for (int m = 0;m < deg;m++)
a[m] = (int *)malloc(sizeof(int)*deg);
for (i = 0;i < deg;i++)
for (j = 0;j < deg;j++)
a[i][j] = 0;
laobo(deg, a, 1);
for (i = 0;i < deg;i++)//A象限赋值
for (j = 0;j < deg;j++)
{
arr[i][j] = a[i][j];
}
for (i = 0;i < deg;i++)
for (j = 0;j < deg;j++)
a[i][j] = 0;
laobo(deg, a, 1+deg*deg);
for (i = 0;i < deg;i++)//D象限赋值
for (j = 0;j < deg;j++)
{
arr[i+deg][j+deg] = a[i][j];
}
for (i = 0;i < deg;i++)
for (j = 0;j < deg;j++)
a[i][j] = 0;
laobo(deg, a, 1 + 2*deg*deg);
for (i = 0;i < deg;i++)//B象限赋值
for (j = 0;j < deg;j++)
{
arr[i][j + deg] = a[i][j];
}
for (i = 0;i < deg;i++)
for (j = 0;j < deg;j++)
a[i][j] = 0;
laobo(deg, a, 1 + 3*deg*deg);
for (i = 0;i < deg;i++)//C象限赋值
for (j = 0;j < deg;j++)
{
arr[i + deg][j] = a[i][j];
}
k = (n - 2) / 4;
for (i = 0;i < deg;i++)//实现了AC象限前k个数的交换
{
for (j = 0;j < k;j++)
{
temp = arr[i][j];
arr[i][j] = arr[i + deg][j];
arr[i + deg][j] = temp;
}
}
for (j = 0;j < k;j++)//因为A象限中间行是从中间格开始换的
//所以我们要将前面替换了的前k格给替换回来
{
temp = arr[deg / 2][j];
arr[deg / 2][j] = arr[deg / 2 + deg][j];
arr[deg / 2 + deg][j] = temp;
}
//替换中间格开始的k个
for (j = deg/2;j <((deg/2) + k);j++)
{
temp = arr[deg / 2][j];
arr[deg / 2][j] = arr[deg / 2 + deg][j];
arr[deg / 2 + deg][j] = temp;
}
if (k != 0)
{
for (i = 0;i < deg;i++)
for (j = deg + deg / 2;j < ((deg + deg / 2) + k - 1);j++)
{
temp = arr[i][j];
arr[i][j] = arr[i + deg][j];
arr[i + deg][j] = temp;
}
}
return 0;
}
int main()
{
int **arr;//二级指针动态申请二维数组
int n;
int i, j;
printf("请输入你想打印几阶幻方:");
scanf("%d",&n);
arr = (int **)malloc(sizeof(int*)*n);//申请一个n*n的二维数组
for (i = 0;i < n;i++)
arr[i] = (int *)malloc(sizeof(int)*n);
for (i = 0;i < n;i++)
for (j = 0;j < n;j++)
arr[i][j] = 0;
if (n % 2 != 0)
{
laobo(n, arr,1);
}
else if (n % 4 == 0)
{
Init(n, arr);
haier(n, arr);
}
else
{
late(n, arr);
}
for (i = 0;i < n;i++)
{
for (j = 0;j < n;j++)
{
printf("%4d", arr[i][j]);
}
printf("\n");
}
return 0;
}
emmm 看不懂私信我吧。。
标签:位置 printf 个数 超出 strong img 赋值 开始 info
原文地址:https://www.cnblogs.com/zty200329/p/10626463.html