标签：方便   分析   最小值   时间复杂度   复杂   下标   www   指针   提前   

输入: nums = [2,5,6,0,0,1,2], target = 0
输出: true
示例 2:
输入: nums = [2,5,6,0,0,1,2], target = 3
输出: false

问题分析

对于数据特点的分析见此链接

https://www.cnblogs.com/FDProcess/p/10614145.html

这道题的变化就是数组内的数据可能存在重复的部分，这就导致了解法的变化。

解法一：找出数组的最小值，对两边分别进行二分搜索

我们依旧可以套用之前搜索最小值的办法找出最小值所在下标，但是最小值可能是重复的，但是和我们之前分析的一样，这个值存在于递增序列B里面，我们在通过二分法找到其中的一个最小值之后，只需要一直向左移动下标，直到移动到最小值第一次出现的位置或移动到数组最左端为止。

对于存在重复数据的情况下寻找最小值的伪代码为：

findMin(nums)
    // nums is a array

    left = 0;
    right = nums.length - 1;

    while left <= right
        mid = (left + right) / 2;
        // 判断是否是最小值，也就是左右都比它大
        if nums[mid] is smaller than left and right values
            break;
        else if nums[mid] > nums[0]
            left = mid + 1;
        else
            right = mid - 1;

    if nums[0] < nums[mid]
        minIndex = 0;
    else
        minIndex = mid;
    
    while minIndex > 0 and nums[minIndex - 1] == nums[minIndex]
        minIndex--;

    return minIndex;

找到最小值后，后续代码不变，进行两次二分搜素即可

search(nums,target)
    /*
        nums is a array
        target is a number
    */

    minIndex = findMin(nums);

    left = 0;
    right = minIndex - 1;

    while left <= right
        mid = (left + right) / 2;
        if nums[mid] == target
            return true;
        else if target < nums[mid]
            right = mid - 1;
        else
            left = mid + 1;

    left = minIndex;
    right = nums.length - 1;

    while left <= right
        mid = (left + right) / 2;
        if nums[mid] == target
            return true;
        else if target < nums[mid]
            right = mid - 1;
        else
            left = mid + 1;

    return false;

时空复杂度分析

函数findMin(nums)时间复杂度为O(n),原因是函数内执行最后一个循环之前minIndex可能在数组的最右端，search(nums, target)函数内部两次二分查找时间复杂度各为O(lgn)，所以算法总时间复杂度为O(n)

空间复杂度O(1)

直接通过二分搜索找到目标值

和数据无重复时不同的是，如果二分点的值和数组最左端的值一样，我们将无法判断二分点所在的为止，具体看下图

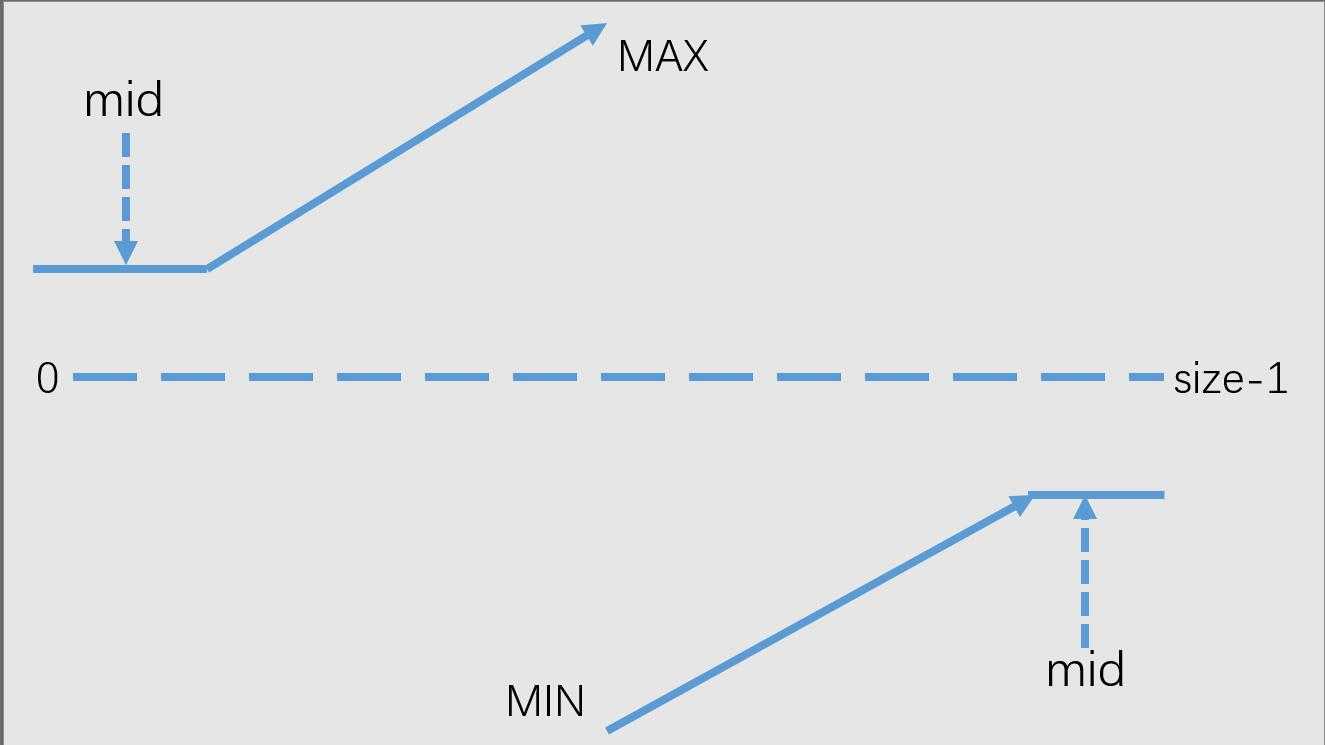
所以这时我们应该想办法让二分点脱离重复值，通过移动左指针右移或者右指针左移来缩小范围，让二分点脱离重复值，方便我们进行判断目标值究竟在二分点的哪一边。
不过不要忘记做右指针在移动的时候可能会经过目标值，所以要提前判断左右指针所指的值是否为目标值

整个程序伪代码为：

search(nums, target)
    /*
        nums is a array
        target is a number
    */

    left = 0;
    right = nums.length - 1;
    if nums[0] == target
        return true;
    if nums[nums.length - 1] == target
        return true;


    while left <= right
        mid = (left + right) / 2;
        if nums[mid] == target
            return true;
        else if nums[left] == target
            return true;
        else
            if nums[mid] > nums[0]
                if target > nums[mid]
                    left = mid + 1;
                else
                    if target > nums[0]
                        right = mid - 1;
                    else
                        left = mid + 1;

            else if nums[mid] < nums[0]
                if target < nums[mid]
                    right = mid - 1;
                else
                    if target < nums[nums.size() - 1]
                        left = mid + 1;
                    else
                        right = mid - 1;
            else
                left++;
    
    return false;

时空复杂度分析

时间复杂度O(n)
空间复杂度O(1)

[LeetCode] 搜索旋转排序数组Ⅱ

标签：方便   分析   最小值   时间复杂度   复杂   下标   www   指针   提前   

原文地址：https://www.cnblogs.com/FDProcess/p/10632301.html