标签:unsigned 否则 out 二分插入 64位 元素 mes tor --
| 时间复杂度(平均) | 时间复杂度 (最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
/* ** 直接插入排序的C++实现 ** 1.设置监视哨r[0],将待插入记录的值赋值给r[0]; ** 2.设置开始查找的位置j; ** 3.在数组中进行搜索,搜索中将第j个记录后移,直至r[0].key≥r[j].key为止; ** 4.将r[0]插入r[j+1]的位置上。 */ void insertSort(vector<int>& seq) { seq.insert(seq.begin(), 0); int length = seq.size(); // 待排序序列的长度 for (int i = 2; i < length; i++) { if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时 seq[0] = seq[i]; // 将待插入的元素移动到首位 int j = i - 1; while (seq[0] < seq[j]) { // 依次将已排好序的元素与待插入元素比较 seq[j + 1] = seq[j]; // 如果待排序元素小于当前元素,当前元素后移一位 j--; } seq[j + 1] = seq[0]; // 将待排序元素插入到正确的位置 } } seq.erase(seq.begin()); }
将直接插入排序中寻找seq[i]的插入位置的方法改为采用折半比较,即可得到折半插入排序算法。在处理seq[i]时,seq[0]……seq[i-1]已经按值排好序。所谓折半比较,就是在插入seq[i]时,取seq[i-1/2]的值与seq[i]的值进行比较,如果seq[i]的值小于seq[i-1/2]的值,则说明seq[i]只能插入seq[0]到seq[i-1/2]之间,故可以在seq[0]到seq[i-1/2-1]之间继续使用折半比较;否则只能插入seq[i-1/2]到seq[i-1]之间,故可以在seq[i-1/2+1]到seq[i-1]之间继续使用折半比较,如此反复,直到最后能够确定插入的位置为止。
/* ** 二分插入排序的C++实现 ** 假设:对N个类型为int的整数值进行排序 ** 每次采用折半查找的方式从已排好序的序列中定位插入位置 ** 当high小于low时,查找结束,在high之后插入待排序的元素 */ void insertSort2(vector<int>& seq) { int wait = seq[0]; int length = seq.size(); // 待排序序列的长度 for (int i = 1; i < length; i++) { if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时 wait = seq[i]; // 保存待插入的元素值到wait int low = 0, high = i - 1, mid = (high + low) / 2; /* 折半查找要插入的位置 */ while (high >= low) { // high大于low时终止查找 if (wait < seq[mid]) high = mid - 1; else low = mid + 1; mid = (high + low) / 2; } for (int j = i - 1; j > high; j--) seq[j + 1] = seq[j]; // 向后移动元素 seq[high + 1] = wait; // 将待排序元素插入到正确的位置 } } }
下面是直接插入排序与二分插入排序的比较,
作者在 Intel i7四核处理器,Linux x86_64位机上测试了10组大小为1000的整数数组的排序,整数的范围在0~100000之间
/* ** 直接插入排序与二分插入排序的比较 ** 数字的规模:10组大小为1000的数组 ** 数字的范围:0~100000之间,随机生成 */ #include<time.h> #include<vector> #include<stdlib.h> #include<iostream> using namespace std; void insertSort(vector<int>& seq) { int wait = seq[0] , j = 0; int length = seq.size(); // 待排序序列的长度 for (int i = 1; i < length; i++) { if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时 wait = seq[i]; // 保存待插入的元素值到wait j = i - 1; while (wait < seq[j]) { // 依次将已排好序的元素与待插入元素比较 seq[j + 1] = seq[j]; // 如果待排序元素小于当前元素,当前元素后移一位 j--; } seq[j + 1] = wait; // 将待排序元素插入到正确的位置 } } } void insertSort2(vector<int>& seq) { int wait = seq[0]; int length = seq.size(); // 待排序序列的长度 for (int i = 1; i < length; i++) { if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时 wait = seq[i]; // 保存待插入的元素值到wait int low = 0, high = i - 1, mid = (high + low) / 2; /* 折半查找要插入的位置 */ while (high >= low) { // high大于low时终止比较 if (wait < seq[mid]) high = mid - 1; else low = mid + 1; mid = (high + low) / 2; } for (int j = i - 1; j > high; j--) seq[j + 1] = seq[j]; // 向后移动元素 seq[high + 1] = wait; // 将待排序元素插入到正确的位置 } } } int main() { vector<int> seq[10]; vector<int> seq_[10]; for (int i = 0; i < 10; i++) { for (int j = 0; j < 1000; j++) seq[i].push_back(rand() % 100000); } for (int i = 0; i < 10; i++) { seq_[i] = seq[i]; } srand((unsigned)time(NULL)); clock_t start1 = clock(); for (int i = 0; i < 10; i++) { insertSort(seq[i]); } clock_t ends1 = clock(); cout << "the algorithm 1 running time : " << (double)(ends1 - start1)/10 / CLOCKS_PER_SEC << endl; clock_t start2 = clock(); for (int i = 0; i < 10; i++) { insertSort2(seq_[i]); } clock_t ends2 = clock(); cout << "the algorithm 2 running time : " << (double)(ends2 - start2)/10 / CLOCKS_PER_SEC << endl; cout << "time 1 / time 2 = " << ((double)(ends1 - start1)/10 / (double)(ends2 - start2)/10)*100 << endl; for (int i = 0; i < 10; i++) { for (int j = 0; j < seq[i].size(); j++) { if (seq_[i][j] - seq[i][j] != 0) { cout << "sorted error!"; break; } } } return 0; }
实验截图:
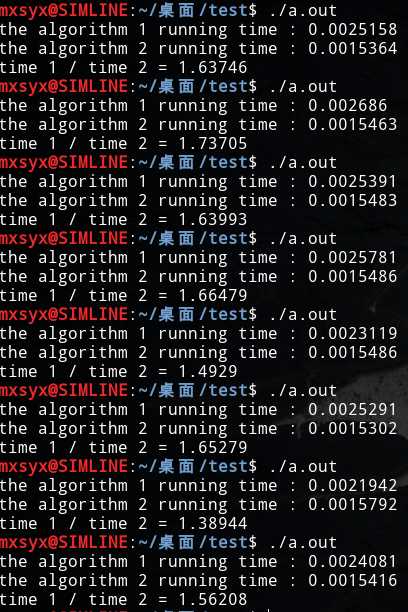
可以看到,二分插入排序比直接插入排序的速度快1.5倍左右,当然受到各方面因素的影响,实验结果未必准确,但采用折半的方式的确节省了不少时间。
标签:unsigned 否则 out 二分插入 64位 元素 mes tor --
原文地址:https://www.cnblogs.com/nkqlhqc/p/9768621.html