3D图形学在游戏开发中的，矩阵，四元数，欧拉角之间的底层转换算法。

标签：角度   格式   pre   技术   实现   ado   tps   oss   四元数   

四元数转矩阵的底层算法：

public Quaternion QuaternionMatrix(float w, float x, float y, float z)
    {
        Matrix4x4 matrix = new Matrix4x4();

        matrix.m00 = 1f - 2 * SetSquare(y) - 2 * SetSquare(z);
        matrix.m01 = 2f * (x * y) - 2f * (w * z);
        matrix.m02 = 2f * (x * z) + 2f * (w * y);
        matrix.m03 = 0.0f;

        matrix.m10 = 2f * (x * y) + 2f * (w * z);
        matrix.m11 = 1f - 2f * SetSquare(x) - 2f * SetSquare(z);
        matrix.m12 = 2f * (y * z) - 2f * (w * x);
        matrix.m13 = 0.0f;

        matrix.m20 = 2f * (x * z) - 2f * (w * y);
        matrix.m21 = 2f * (y * z) + 2f * (w * x);
        matrix.m22 = 1f - 2f * SetSquare(x) - 2f * SetSquare(y);
        matrix.m23 = 0.0f;

        matrix.m30 = 0.0f;
        matrix.m31 = 0.0f;
        matrix.m32 = 0.0f;
        matrix.m33 = 0.0f;

        float qw = Mathf.Sqrt(1f + matrix.m00 + matrix.m11 + matrix.m22) / 2;
        float wq = 4 * qw;
        float qx = (matrix.m21 - matrix.m12) / wq;
        float qy = (matrix.m02 - matrix.m20) / wq;
        float qz = (matrix.m10 - matrix.m01) / wq;
        return new Quaternion(qx, qy, qz, qw);
    }

矩阵转四元数的底层算法：

 public Quaternion MatrixToQuaternion(Matrix4x4 matrix)
    {
        float qw = Mathf.Sqrt(1f + matrix.m00 + matrix.m11 + matrix.m22) / 2;
        float w = 4 * qw;
        float qx = (matrix.m21 - matrix.m12) / w;
        float qy = (matrix.m02 - matrix.m20) / w;
        float qz = (matrix.m10 - matrix.m01) / w;
        return new Quaternion(qx, qy, qz, qw);
    }

四元数转欧拉角的底层算法实现：
这里的四元数转欧拉角我要特别做一下说明，这里我有四种实现方式，其中有三种是解决个别角度问题的

可以直接拿去用的算法

public Vector3 QauToE4(float x_, float y_, float z_, float w_)
    {

>         float check = 2.0f * (-y_ * z_ + w_ * x_);****
        if (check < -0.995f)
        {
            return new Vector3(
                -90.0f,
                0.0f,
                -Mathf.Atan2(2.0f * (x_ * z_ - w_ * y_), 1.0f - 2.0f * (y_ * y_ + z_ * z_)) * M_RADTODEG
            );
        }
        else if (check > 0.995f)
        {
            return new Vector3(
                90.0f,
                0.0f,
                Mathf.Atan2(2.0f * (x_ * z_ - w_ * y_), 1.0f - 2.0f * (y_ * y_ + z_ * z_)) * M_RADTODEG
            );
        }
        else
        {
            return new Vector3(
              Mathf.Asin(check) * M_RADTODEG,
                Mathf.Atan2(2.0f * (x_ * z_ + w_ * y_), 1.0f - 2.0f * (x_ * x_ + y_ * y_)) * M_RADTODEG,
                Mathf.Atan2(2.0f * (x_ * y_ + w_ * z_), 1.0f - 2.0f * (x_ * x_ + z_ * z_)) * M_RADTODEG
            );
        }
    }

解决个别角度问题的算法

public Vector3 QuaToE(float x, float y, float z, float w)
    {
        float h, p, b;

        float sp = -2.0f * (y * z + w * x);
        if (Mathf.Abs(sp) > 0.9999f)
        {
            p = 1.570796f * sp;

            h = Mathf.Atan2(-x * z - w * y, 0.5f - y * y - z * z);
            b = 0.0f;
        }
        else
        {
            p = Mathf.Asin(sp);
            h = Mathf.Atan2(x * z - w * y, 0.5f - x * x - y * y);
            b = Mathf.Atan2(x * y - w * z, 0.5f - x * x - z * z);
        }
        return new Vector3(h, p, b);
    }

    public Vector3 QuaToE2(float x, float y, float z, float w)
    {
        float h, p, b;
        float sp = -2.0f * (y * z - w * x);

        if (Mathf.Abs(sp) > 0.9999f)
        {
            p = 1.570796f * sp;
            h = Mathf.Atan2(-x * z + w * y, 0.5f - y * y - z * z);
            b = 0.0f;
        }
        else
        {
            p = Mathf.Asin(sp);
            h = Mathf.Atan2(x * z + w * y, 0.5f - x * x - y * y);
            b = Mathf.Atan2(x * y + w * z, 0.5f - x * x - z * z);
        }
        return new Vector3(h, p, b);
    }
    public Vector3 QauToE3(float x, float y, float z, float w)
    {

        Vector3 euler;
        const float Epsilon = 0.0009765625f;
        const float Threshold = 0.5f - Epsilon;

        float TEST = w * y - x * z;

        if (TEST < -Threshold || TEST > Threshold) // 奇异姿态,俯仰角为±90°
        {
            float sign = Mathf.Sign(TEST);

            euler.z = -2 * sign * (float)Mathf.Atan2(x, w); // yaw

            euler.y = sign * (float)(3.1415926f / 2.0); // pitch

            euler.x = 0; // roll

        }
        else
        {
            euler.x = Mathf.Atan2(2 * (y * z + w * x), w * w - x * x - y * y + z * z);
            euler.y = Mathf.Asin(-2 * (x * z - w * y));
            euler.z = Mathf.Atan2(2 * (x * y + w * z), w * w + x * x - y * y - z * z);
        }
        return euler;
    }

欧拉角转四元数算法：

public Quaternion E4ToQua(float x, float y, float z)
    {
        float w_, x_, y_, z_;
        x *= M_DEGTORAD_2;
        y *= M_DEGTORAD_2;
        z *= M_DEGTORAD_2;
        float sinX = Mathf.Sin(x);
        float cosX = Mathf. Cos(x);
        float sinY = Mathf.Sin(y);
        float cosY = Mathf.Cos(y);
        float sinZ = Mathf.Sin(z);
        float cosZ = Mathf.Cos(z);

        w_ = cosY * cosX * cosZ + sinY * sinX * sinZ;
        x_ = cosY * sinX * cosZ + sinY * cosX * sinZ;
        y_ = sinY * cosX * cosZ - cosY * sinX * sinZ;
        z_ = cosY * cosX * sinZ - sinY * sinX * cosZ;
        return new Quaternion(x_, y_, z_, w_);
    }

算法测试：
这里使用的unity进行的测试，不过这里提供的算法是通用的。

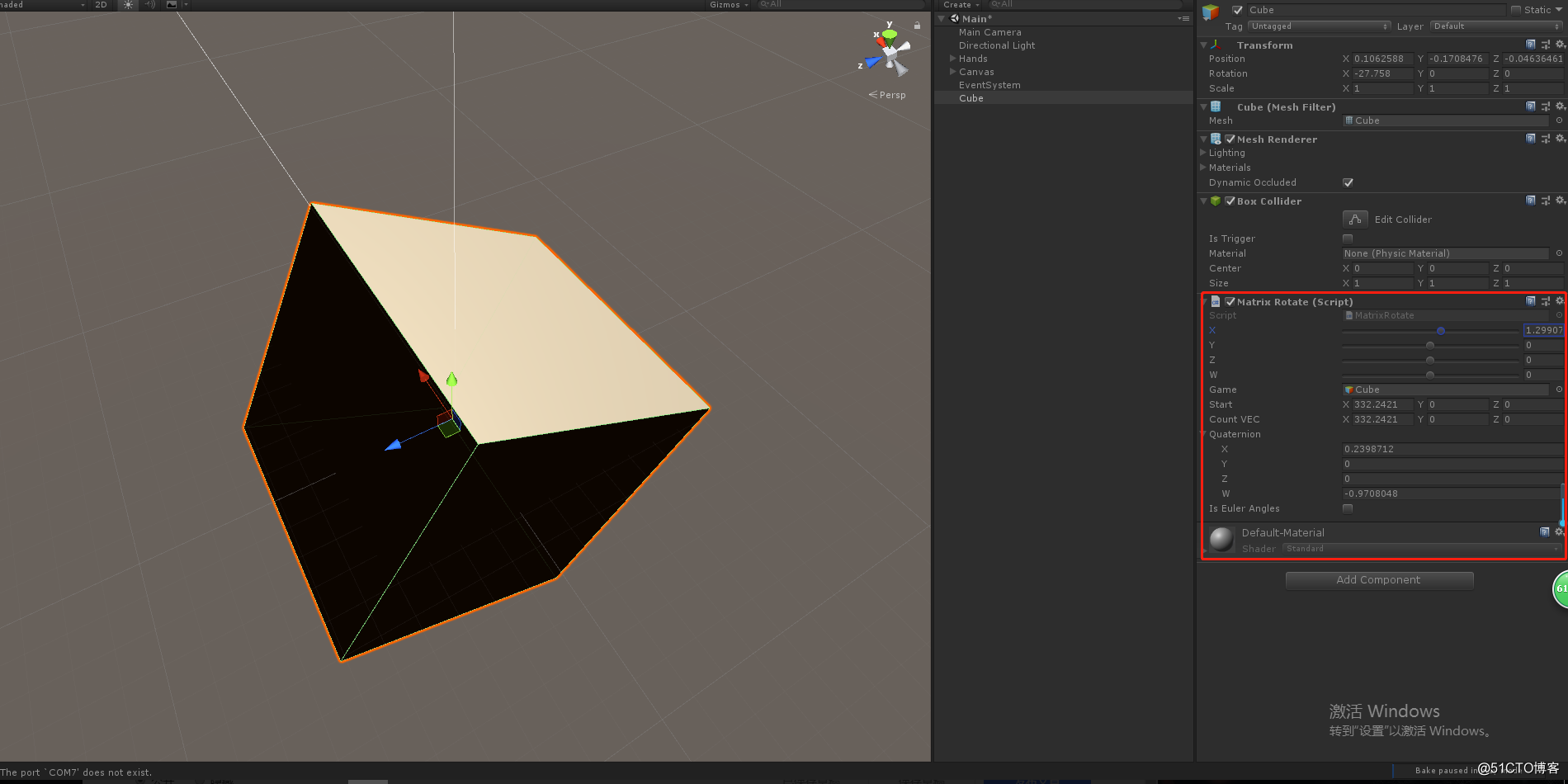
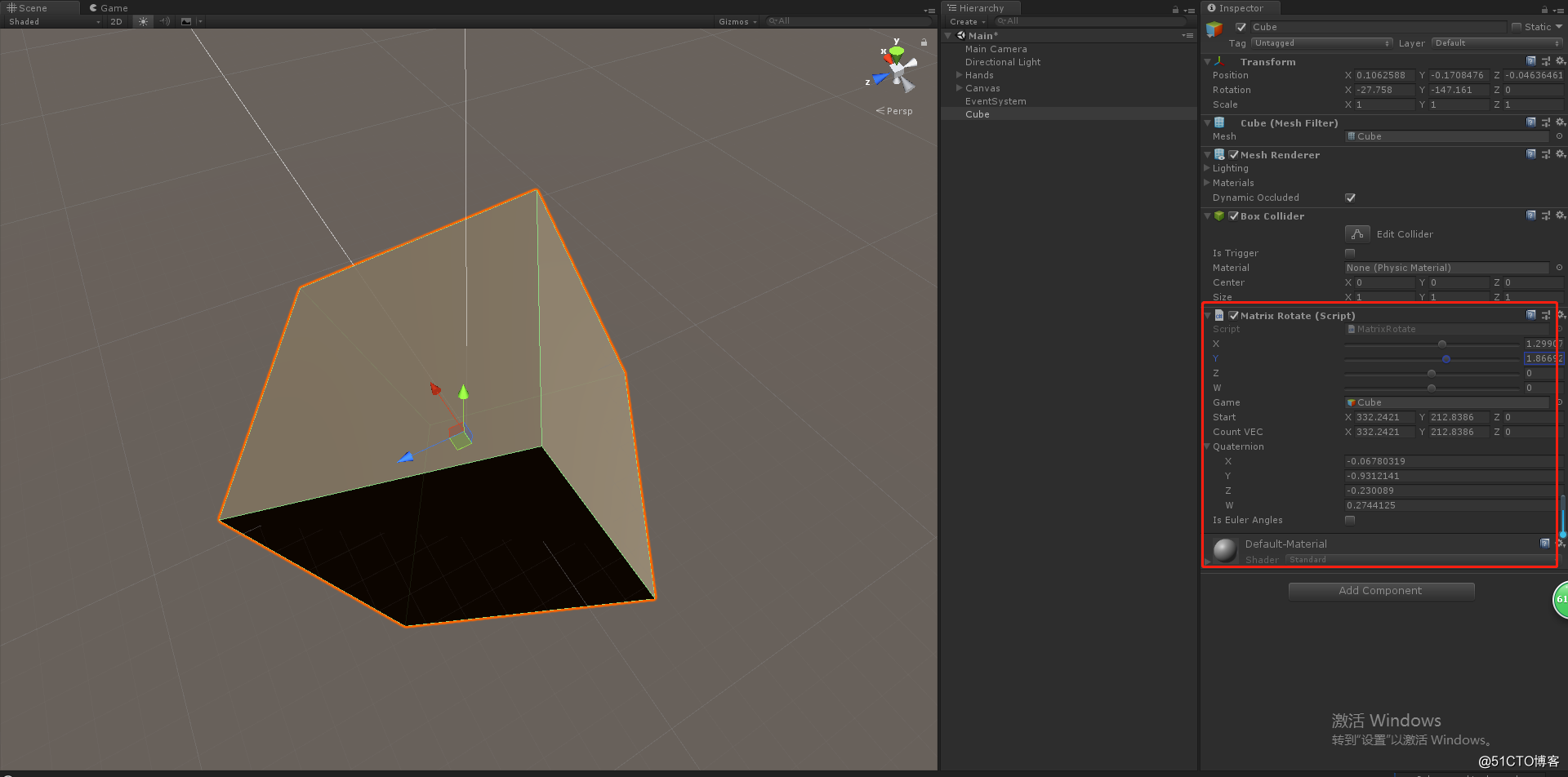
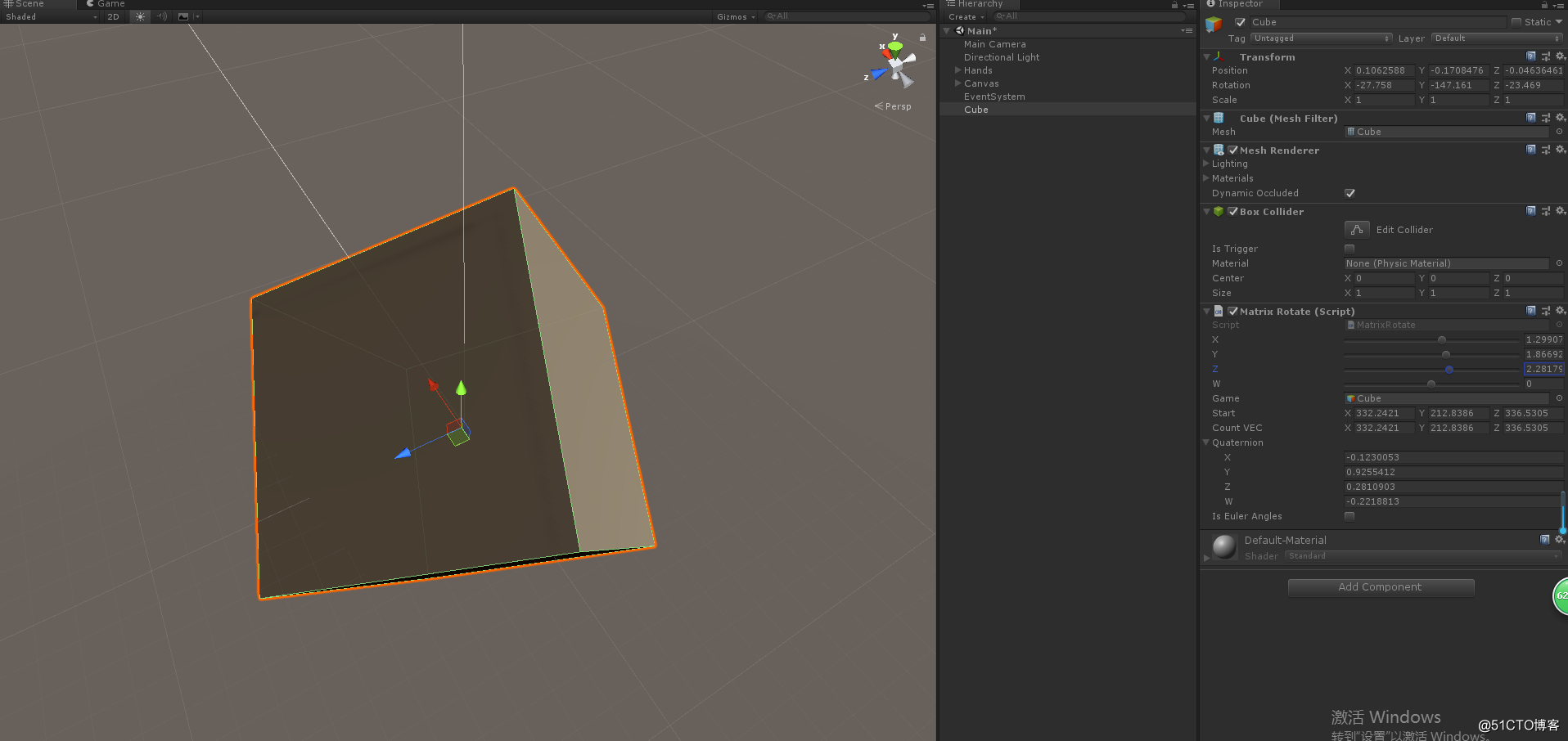
3D图形学在游戏开发中的，矩阵，四元数，欧拉角之间的底层转换算法。

标签：角度   格式   pre   技术   实现   ado   tps   oss   四元数   

原文地址：https://blog.51cto.com/14058389/2372889