标签:ima 初始化 入队 获得 队列的实现 输入 析构函数 color 部分
1、循环队列的实现(请采用模板类及模板函数实现)
[实现提示] 同时可参见教材p65-p67页的ADT描述及算法实现及ppt)函数、类名称等可自定义,部分变量请加上学号后3位。也可自行对类中所定义的操作进行扩展。
所加载的库函数或常量定义及类的定义:
#include<stdlib.h> #include<iostream> using namespace std; typedef int DataType; class SeqQueue{ private: DataType *data; //顺序队列数组 int front; //队头指示器 int rear; //队尾指示器 int count; //元素个数计数器 int maxsize; public: SeqQueue(int size); //构造函数 ~SeqQueue(void){}; //析构函数 void Append(const DataType& item); //入队列 DataType Delete(void); //出队列 DataType GetFront(void)const; //取队头数据元素 int GetCount(); //得到队列的元素个数 int NotEmpty(void)const //非空否 {return count!=0;} void GetAll(); //得到所有元素 void DeleteAll(); //删除所有 };
(1)构造一个空的循环队列
输入:队列元素存储区域的大小size;
动作:初始化队列,队头及队尾指示器,申请存储队列的数组,设置队列存储区域的大小maxsize
SeqQueue::SeqQueue(int size) { front=rear=0; count=0; maxsize=size; data=new DataType[maxsize]; };
(2)入队操作算法实现:
输入:要入队的元素x;
前置条件:队列未满
动作:把x插入队尾
输出:无
后置条件:队列中增加了一个元素
void SeqQueue::Append(const DataType& item) //入队列 //把数据元素item插入队列作为当前的新队尾 { if(count>0&&front==rear) { cout<<"队列已满!"<<endl; exit(0); } data[rear]=item; //把元素item加在队尾 rear=(rear+1) % maxsize; //队尾指示器加1 count++; //计数器加1 }
(3)求队列的元素个数算法
输入:无
前置条件:无;
动作:求队列的元素个数,含表空返回个数为零的情况。
输出:返回队列的元素个数。
int SeqQueue::GetCount() { return count; }
(4)出队操作算法
输入:无
前置条件:队列非空
动作:删除队头元素
输出:返回队头元素的值
后置条件:队列中删除了一个元素
DataType SeqQueue::Delete(void) //出队列 //把队头元素出队列,出队列元素由函数返回 { if(count==0) { cout<<"队列已空!"<<endl; exit(0); } DataType temp=data[front]; //保存原队头元素 front=(front+1) % maxsize; //队头指示器加1 count--; //计数器减1 return temp; //返回原队头元素 }
(5)遍历队列算法
输入:无
前置条件:队列非空
动作:输出队列中的各元素
输出:无
后置条件:无
void SeqQueue::GetAll() { if(count==0) { cout<<"队列已空!"<<endl; exit(0); } for(int i=0;i<GetCount();i++) cout<<data[i]<<" "; }
(6)清空队列算法
输入:无
前置条件:队列存在
动作:释放队列的存储空间
输出:无
后置条件:队列不存在
void SeqQueue::DeleteAll() { delete[] data; count=0; }
(7)判队列为空算法
输入:无
前置条件:队列存在
动作:判是否为空
输出:空返回1,否则返回0
后置条件:无
int NotEmpty(void)const //非空否 {return count!=0}
(8)获得队列头结点
输入:无
前置条件:队列存在
动作:获得队头的元素
输出:返回队头的元素值
后置条件:无
DataType SeqQueue::GetFront(void)const //取队头数据元素 //取队头元素并由函数返回 { if(count==0) { cout<<"队列已空!"<<endl; exit(0); } return data[front]; //返回队头元素 }
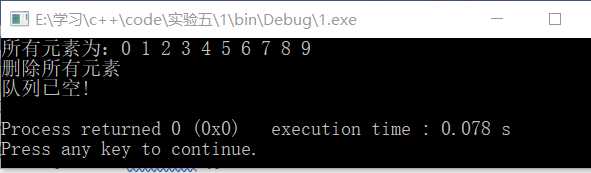
运行结果:
节点类
template <class T> class LinQueue; //前视定义,否则友元无法定义 template <class T> class QueueNode { friend class LinQueue <T>; //定义类LinQueue<T>为友元private: QueueNode <T> *next; //指针 T data; //数据元素 public: QueueNode(const T& item,QueueNode <T> *ptrNext=NULL) {data=item;next=ptrNext;} //构造函数 ~QueueNode(){}; //析构函数 };
队列类头文件和类定义
#include<stdlib.h> #include<iostream> #include"QueueNode.h" using namespace std; template <class T> class LinQueue { private: QueueNode <T> *front; //队头指针 QueueNode <T> *rear; //队尾指针 int count; //计数器 public: LinQueue(void); //构造函数 LinQueue(T a[],int n); ~LinQueue(void); //析构函数 void Append(const T& item); //入队列 T Delete(void); //出队列 T GetFront(void)const; //取队头数据元素 void ClearAll(); //清空队列 void GetAll(); //遍历所有元素 int GetCount(); //得到队列元素个数 int NotEmpty(void)const //非空否 {return count!=0;} };
(1)初始化链式空队列
关键动作:初始化队列,设置队头及队尾指示器。
template <class T> LinQueue <T>::LinQueue() //构造函数 { front=rear=NULL; //链式队列无头结点 count=0; //count的初值为0 }
(2)带参数的构造函数,实现创建链式队列
输入:存储放初始数据元素的数组a[],元素个数n
前置条件:队列不存在
动作:把a中的数据元素依次插入队尾
输出:无
后置条件:队列中有n个元素入队
template <class T> LinQueue <T>::LinQueue(T a[],int n) { front=rear=NULL; //链式队列无头结点 count=0; //count的初值为0 for(int i=0;i<n;i++) { Append(a[i]); } }
(3)入队操作算法
输入:要入队的元素x;
前置条件:队列未满
动作:把x插入队尾
输出:无
后置条件:队列中增加了一个元素
template <class T> void LinQueue <T>::Append(const T& item) //入队列 //把数据元素item插入队列作为新队尾结点 { //构造新结点newNode,newNode的data域值为item,next域值为NULL QueueNode <T> *newNode=new QueueNode <T>(item,NULL); if(rear!=NULL) rear->next=newNode; //新结点链入 rear=newNode; //队尾指针指向新队尾结点 //若队头指针原先为空则置为指向新结点 if(front==NULL) front=newNode; count++; //计数器加1 }
(4)出队操作算法
输入:无
前置条件:队列非空
动作:删除队头元素
输出:返回队头元素的值
后置条件:队列中删除了一个元素
template <class T> T LinQueue <T>::Delete(void) //出队列 //把队头结点删除并由函数返回 { if(count==0) { cout<<"队列已空!"<<endl; exit(0); } QueueNode <T> *p=front->next; //p指向新的队头结点 T data=front->data; //保存原队头结点的data域值 delete front; //释放原队头结点空间 front=p; //front指向新的对头结点 count--; //计数器减1 return data; //返回原队头结点的data域值 }
(5)清空队列算法
输入:无
前置条件:队列存在
动作:释放队列的存储空间
输出:无
后置条件:队列不存在
void LinQueue <T>::ClearAll() { QueueNode <T> *p,*q; p=front; //p指向第一个结点 while(p!=NULL) //循环直至全部结点空间释放 { q=p; p=p->next; delete q; } count=0; //置为初始化值0 front=rear=NULL; }
(6)判队列为空算法
输入:无
前置条件:队列存在
动作:判是否为空
输出:空返回1,否则返回0
后置条件:无
int NotEmpty(void)const //空否 {return count==0;}
(7)获得队列头结点
输入:无
前置条件:队列存在
动作:获得队头的元素
输出:返回队头的元素值
后置条件:无
template <class T> T LinQueue <T>::GetFront(void)const //取队头数据元素 { if(count==0) { cout<<"队列已空!"<<endl; exit(0); } return front->data; }
(8)遍历队列中的元素
输入:无
前置条件:队列非空
动作:输出队列中的各元素
输出:无
后置条件:无
void LinQueue <T>::GetAll() { if(count==0) { cout<<"队列为空!"<<endl; exit(0); } QueueNode <T> *p; p=front; //p指向第一个结点 cout<<"当前所有元素:"; while(p!=NULL) //循环直至全部结点遍历 { cout<<p->data<<" "; p=p->next; } cout<<endl; }
(9)求队列数据元素个数
输入:无
前置条件:无;
动作:求队列的元素个数,含表空返回个数为零的情况。
输出:返回队列的元素个数。
template <class T> int LinQueue <T>::GetCount() { return count; }
测试数据
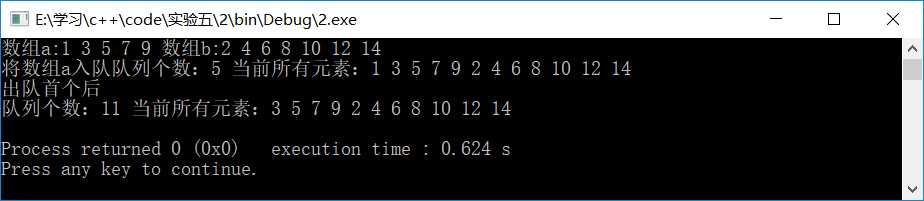
#include <iostream> #include"LinQueue.h" using namespace std; int main() { int a[]={1,3,5,7,9}; int b[]={2,4,6,8,10,12,14}; int d=sizeof(a)/sizeof(a[0]); int c=sizeof(b)/sizeof(b[0]); cout<<"数组a:"; for(int i=0;i<d;i++) cout<<a[i]<<" "; cout<<"数组b:"; for(int i=0;i<c;i++) cout<<b[i]<<" "; cout<<"\n将数组a入队"; LinQueue<int>q1335(a,5); cout<<"队列个数:"<<q1335.GetCount()<<" "; for(int i=0;i<c;i++) q1335.Append(b[i]); q1335.GetAll(); q1335.Delete(); cout<<"出队首个后\n队列个数:"<<q1335.GetCount()<<" "; q1335.GetAll(); return 0; }
结果
标签:ima 初始化 入队 获得 队列的实现 输入 析构函数 color 部分
原文地址:https://www.cnblogs.com/cc123nice/p/10663183.html