标签:|| ble 初始 算法 ext png 组合数 超过 全排列
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
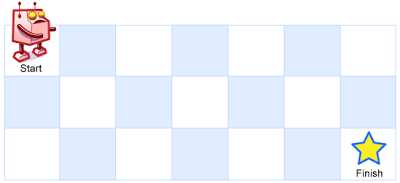

例如,上图是一个7 x 3 的网格。有多少可能的路径?
说明:m 和 n 的值均不超过 100。
示例 1:
输入: m = 3, n = 2 输出: 3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向右 -> 向下 2. 向右 -> 向下 -> 向右 3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3 输出: 28
1 #include "_000库函数.h" 2 3 4 // 第一想法就是当成排列组合来做 5 // 产生初始数组,向右为1,向下为2 6 // 方案可行,但超出时间限制了 7 class solution { 8 public: 9 int uniquepaths(int m, int n) { 10 vector<int>v(m-1,1);//m-1个向右 11 v.insert(v.end(), n - 1, 2);//n-1个向下 12 int nums = 1; 13 while (next_permutation(v.begin(), v.end()))nums++; 14 return nums; 15 } 16 }; 17 18 //看过博客后,才发现,带重复数字的全排列组合数就是较小的数的取法数目 19 class solution { 20 public: 21 int uniquepaths(int m, int n) { 22 int min = m > n ? n : m; 23 double res = 1, denom = 1; 24 for (int i = 1; i <= min - 1; ++i) { 25 res *= m + n - 1 - i; 26 denom *= i; 27 } 28 return (int) (res / denom); 29 } 30 }; 31 32 //用递归不知道会不会快一点 33 // 超时了 34 35 class solution { 36 public: 37 int uniquepaths(int m, int n) { 38 return combin(1, 1, m, n); 39 } 40 int combin(int row, int col, int m, int n) { 41 if (row == m && col == n)//到达右下角 42 return 1; 43 if (row > m || col > n)//不满足要求 44 return 0; 45 return combin(row + 1, col, m, n) + combin(row, col + 1, m, n); 46 } 47 48 }; 49 50 //使用动态规划 51 //那么跟爬梯子问题一样,我们需要用动态规划Dynamic Programming来解, 52 //我们可以维护一个二维数组dp,其中dp[i][j]表示到当前位置不同的走法的个数, 53 //然后可以得到递推式为: dp[i][j] = dp[i - 1][j] + dp[i][j - 1], 54 //这里为了节省空间,我们使用一维数组dp,一行一行的刷新也可以,代码如下: 55 class Solution { 56 public: 57 int uniquePaths(int m, int n) { 58 vector<int> dp(n, 1); 59 for (int i = 1; i < m; ++i) { 60 for (int j = 1; j < n; ++j) { 61 dp[j] += dp[j - 1]; 62 } 63 } 64 return dp[n - 1]; 65 } 66 }; 67 68 void T062() { 69 Solution s; 70 cout << s.uniquePaths(7, 3) << endl; 71 }
标签:|| ble 初始 算法 ext png 组合数 超过 全排列
原文地址:https://www.cnblogs.com/zzw1024/p/10663144.html