相关表和相关图可反映两个变量之间的相互关系及其相关方向,但无法确切地表明两个变量之间相关的程度。于是,著名统计学家卡尔·皮尔逊设计了统计指标——相关系数(Correlation coefficient)。相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度;着重研究线性的单相关系数。
百度百科:http://baike.baidu.com/view/172091.htm
在统计学中,皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs[1], 文章中常用r或Pearson‘s r表示)用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。在自然科学领域中,该系数广泛用于度量两个变量之间的相关程度。它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来的。[2][3]这个相关系数也称作“皮尔森相关系数r”。
Wikipedia:http://zh.wikipedia.org/zh/皮尔逊积矩相关系数
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:

以上方程定义了总体相关系数, 一般表示成希腊字母ρ(rho)。基于样本对协方差和标准差进行估计,可以得到样本相关系数, 一般表示成r:
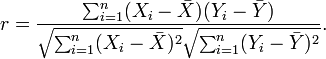
一种等价表达式的是表示成标准分的均值。基于(Xi, Yi)的样本点,样本皮尔逊系数是

其中
 、
、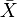 及
及 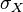
Wikipedia:http://zh.wikipedia.org/zh/皮尔逊积矩相关系数
百度百科:http://baike.baidu.com/view/172091.htm
/**
*
*/
package numerator.pearson.conefficient;
import java.util.ArrayList;
import java.util.List;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
/**
* @author alan-king
*
* the class is going to calculate the numerator;
*
*
*/
public class NumeratorCalculate {
//add global varieties
protected List<String> xList , yList;
public NumeratorCalculate(List<String> xList ,List<String> yList){
this.xList = xList;
this.yList = yList;
}
/**
* add operate method
*/
public double calcuteNumerator(){
double result =0.0;
double xAverage = 0.0;
double temp = 0.0;
int xSize = xList.size();
for(int x=0;x<xSize;x++){
temp += Double.parseDouble(xList.get(x));
}
xAverage = temp/xSize;
double yAverage = 0.0;
temp = 0.0;
int ySize = yList.size();
for(int x=0;x<ySize;x++){
temp += Double.parseDouble(yList.get(x));
}
yAverage = temp/ySize;
//double sum = 0.0;
for(int x=0;x<xSize;x++){
result+=(Double.parseDouble(xList.get(x))-xAverage)*(Double.parseDouble(yList.get(x))-yAverage);
}
return result;
}
}
/**
*
*/
package numerator.pearson.conefficient;
import java.util.List;
/**
* @author alan-king
*
*/
public class DenominatorCalculate {
//add denominatorCalculate method
public double calculateDenominator(List<String> xList,List<String> yList){
double standardDifference = 0.0;
int size = xList.size();
double xAverage = 0.0;
double yAverage = 0.0;
double xException = 0.0;
double yException = 0.0;
double temp = 0.0;
for(int i=0;i<size;i++){
temp += Double.parseDouble(xList.get(i));
}
xAverage = temp/size;
for(int i=0;i<size;i++){
temp += Double.parseDouble(yList.get(i));
}
yAverage = temp/size;
for(int i=0;i<size;i++){
xException += Math.pow(Double.parseDouble(xList.get(i))-xAverage,2);
yException += Math.pow(Double.parseDouble(yList.get(i))-yAverage, 2);
}
//calculate denominator of
return standardDifference = Math.sqrt(xException*yException);
}
}
/**
*
*/
package numerator.pearson.conefficient;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
/**
* @author alan-king
*
*/
public class CallClass {
public static void main(String[] args) throws IOException{
double CORR = 0.0;
List<String> xList = new ArrayList<String>();;
List<String> yList = new ArrayList<String>();
System.out.println("Please input your X's varieties and Y's varieties\r"+
"differnt line,then you should key into \"s\" to end the inputing operator!");
//initial varieties for xList,yList;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String str =null;
boolean flag = false;
while(!(str=br.readLine()).equals("s")){
String[] vStr = str.split(",");
int size = vStr.length;
if(flag == false){
for(int i=0;i<size;i++){
xList.add(i, vStr[i]);
}
flag = true;
}else if(flag == true){
for(int i=0;i<size;i++){
yList.add(i, vStr[i]);
}
flag = false;
}
}
NumeratorCalculate nc = new NumeratorCalculate(xList,yList);
double numerator = nc.calcuteNumerator();
DenominatorCalculate dc = new DenominatorCalculate();
double denominator = dc.calculateDenominator(xList, yList);
CORR = numerator/denominator;
System.out.println("We got the result by Calculating:");
System.out.printf("CORR = "+CORR);
}
}

Pearson product-moment correlation coefficient in java(java的简单相关系数算法)
原文地址:http://blog.csdn.net/anglebeat/article/details/40299273