标签:child 定义 插入 查找 || png 最大 opened click
红黑树介绍
红黑树(Red-Black Tree),它一种特殊的二叉查找树。
红黑树是特殊的二叉查找树,意味着它满足二叉查找树的特征:任意一个节点所包含的键值,大于等于左孩子的键值,小于等于右孩子的键值。
红黑树的每个节点上都有存储位表示节点的颜色,颜色是红(Red)或黑(Black)。
红黑树的特性:
关于红黑树,需要注意的是:
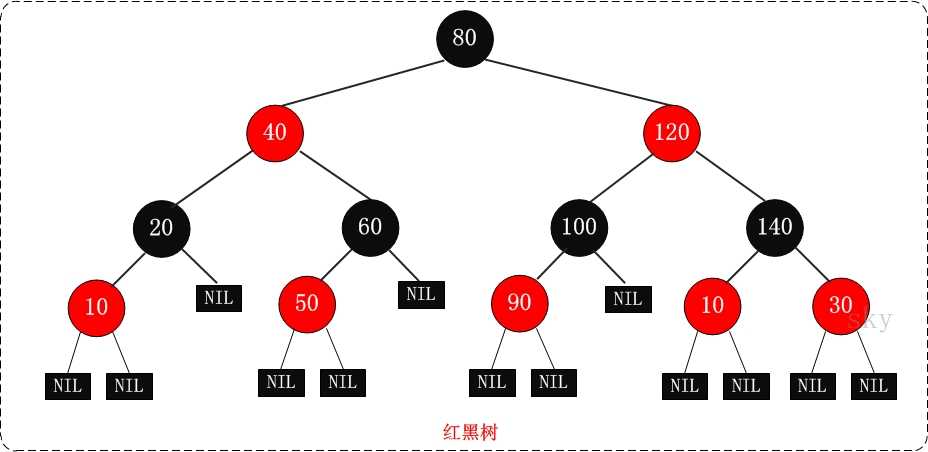
红黑树的基本操作
红黑树的基本操作是添加、删除和旋转。在对红黑树进行添加或删除后,会用到旋转方法。因为添加或删除红黑树中的节点之后,红黑树会发生变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了。而通过旋转,可以使这颗树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。
旋转包括两种:左旋 和 右旋。下面分别图解对红黑树的基本操作进行介绍。
左旋、右旋操作
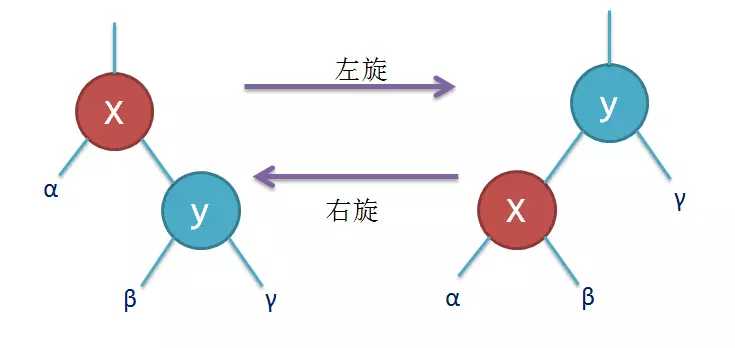
对x进行左旋,意味着"将x变成一个左节点"。
对y进行右旋,意味着"将y变成一个右节点"。

// 左旋转过程 // node x // / \ 左旋转 / // T1 x -----> node T3 // / \ / // T2 T3 T1 T2 private TreeNode leftRotate(TreeNode node) { TreeNode x = node.rightChild; // 左旋转 node.rightChild = x.leftChild; x.leftChild = node; x.color = node.color; node.color = RED; return x; } // 右旋转过程 // node x // / \ 右旋转 / // x T1 -----> y node // / \ / // y T2 T1 T2 private TreeNode rightRotate(TreeNode node) { TreeNode x = node.leftChild; // 右旋转 node.leftChild = x.rightChild; x.rightChild = node; x.color = node.color; node.color = RED; return x; }
颜色翻转操作
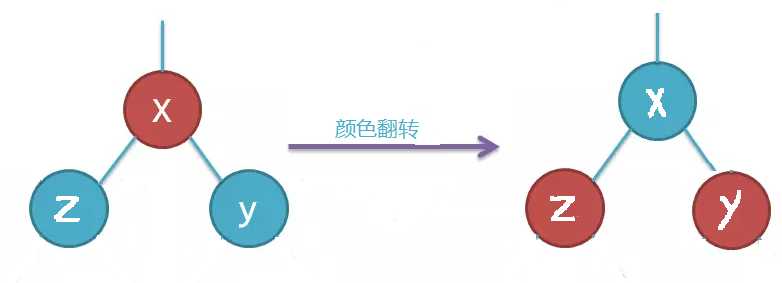

// 颜色翻转 private void flipColors(TreeNode node) { node.color = RED; node.leftChild.color = BLACK; node.rightChild.color = BLACK; }
添加操作
将一个节点插入到红黑树中的步骤:

// 向红黑树中添加节点 public void add(int data) { root = add(root, data); root.color = BLACK; } // 添加节点后返回红黑树的根节点 public TreeNode add(TreeNode node, int data) { if (node == null) { TreeNode treeNode = new TreeNode(data); return treeNode; } else { if (data < node.data) { node.leftChild = add(node.leftChild, data); } else if (data > node.data) { node.rightChild = add(node.rightChild, data); } else { node.data = data; } // node // // 红 if (isRED(node.rightChild) && !isRED(node.leftChild)) { node = leftRotate(node); } // node // / // 红 // / // 红 if (isRED(node.leftChild) && isRED(node.leftChild.leftChild)) { node = rightRotate(node); } // node // / // 红 红 if (isRED(node.leftChild) && isRED(node.rightChild)) { flipColors(node); } return node; } }
查找操作

// 查找节点 public TreeNode search(int data) { TreeNode current = root; while (current.data != data) { if (data < current.data) { current = current.leftChild; } else { current = current.rightChild; } if (current == null) { return null; } } return current; }
删除操作
将红黑树内的某一个节点删除的步骤

/* * 删除结点(node),并返回被删除的结点 */ private void remove(TreeNode node) { TreeNode child, parent; boolean color; // 被删除节点的左右孩子都不为空时 if ( (node.leftChild!=null) && (node.rightChild!=null) ) { // 被删节点的后继节点取代"被删节点"的位置,然后再将被删节点去掉。 TreeNode replace = node; // 获取后继节点 replace = replace.rightChild; while (replace.leftChild != null) replace = replace.leftChild; // node不是根节点 if (parentOf(node)!=null) { if (parentOf(node).leftChild == node) parentOf(node).leftChild = replace; else parentOf(node).rightChild = replace; } else { // node是根节点,更新根节点。 this.root = replace; } // child是取代节点的右孩子,也是需要调整的节点。 // 取代节点肯定不存在左孩子,因为它是一个后继节点。 child = replace.rightChild; parent = parentOf(replace); // 保存取代节点的颜色 color = colorOf(replace); // 被删除节点是它的后继节点的父节点 if (parent == node) { parent = replace; } else { // child不为空 if (child!=null) setParent(child, parent); parent.leftChild = child; replace.rightChild = node.rightChild; setParent(node.rightChild, replace); } replace.parent = node.parent; replace.color = node.color; replace.leftChild = node.leftChild; node.leftChild.parent = replace; if (color == BLACK) removeFixUp(child, parent); node = null; return ; } if (node.leftChild !=null) { child = node.leftChild; } else { child = node.rightChild; } parent = node.parent; // 保存取代节点的颜色 color = node.color; if (child!=null) child.parent = parent; // node不是根节点 if (parent!=null) { if (parent.leftChild == node) parent.leftChild = child; else parent.rightChild = child; } else { this.root = child; } if (color == BLACK) removeFixUp(child, parent); node = null; } public void remove(int data) { TreeNode node; if ((node = search(data)) != null) remove(node); } /* * 红黑树删除修正函数 * 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数; * 目的是将它重新塑造成一颗红黑树。 */ private void removeFixUp(TreeNode node, TreeNode parent) { TreeNode other; while ((node==null || isBlack(node)) && (node != this.root)) { if (parent.leftChild == node) { other = parent.rightChild; if (isRed(other)) { //x的兄弟是红色的 setBlack(other); setRed(parent); leftRotate(parent); other = parent.rightChild; } if ((other.leftChild==null || isBlack(other.leftChild)) && (other.rightChild==null || isBlack(other.rightChild))) { //x的兄弟是黑色,且兄弟的两个孩子也是黑色的 setRed(other); node = parent; parent = parentOf(node); } else { if (other.rightChild==null || isBlack(other.rightChild)) { //x的兄弟是黑色的,并且兄弟的左孩子是红色,右孩子为黑色。 setBlack(other.leftChild); setRed(other); rightRotate(other); other = parent.rightChild; } //x的兄弟是黑色的;并且兄弟的右孩子是红色的,左孩子任意颜色。 setColor(other, colorOf(parent)); setBlack(parent); setBlack(other.rightChild); leftRotate(parent); node = this.root; break; } } else { other = parent.leftChild; if (isRed(other)) { //x的兄弟是红色的 setBlack(other); setRed(parent); rightRotate(parent); other = parent.leftChild; } if ((other.leftChild==null || isBlack(other.leftChild)) && (other.rightChild==null || isBlack(other.rightChild))) { //x的兄弟是黑色,且兄弟的两个孩子也都是黑色的 setRed(other); node = parent; parent = parentOf(node); } else { if (other.leftChild==null || isBlack(other.leftChild)) { // x的兄弟是黑色的,并且兄弟的左孩子是红色,右孩子为黑色。 setBlack(other.rightChild); setRed(other); leftRotate(other); other = parent.leftChild; } // x的兄弟是黑色的;并且兄弟的右孩子是红色的,左孩子任意颜色。 setColor(other, colorOf(parent)); setBlack(parent); setBlack(other.leftChild); rightRotate(parent); node = this.root; break; } } } if (node!=null) setBlack(node); }
红黑树性能总结
1.对于完全随机的数据,普通的二叉搜索树效率较高,但极端下会退化成链表;
2.对于查询较多的情况,AVL树效率较高;
3.红黑树牺牲了平衡性,综合增删改查的所有操作,红黑树的统计性能较优。
标签:child 定义 插入 查找 || png 最大 opened click
原文地址:https://www.cnblogs.com/ericz2j/p/10751507.html