标签:数据交换 blank 选择 10g 一个 aik tar 外部排序 归并
一 定义
外部排序指的是大文件的排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序整个文件的目的。
二 处理过程
(1)按可用内存的大小,把外存上含有n个记录的文件分成若干个长度为L的子文件,把这些子文件依次读入内存,并利用有效的内部排序方法对它们进行排序,再将排序后得到的有序子文件(又称归并段)重新写入外存;
(2)对这些有序子文件逐趟归并,使其逐渐由小到大,直至得到整个有序文件为止。
先从一个例子来看外排序中的归并是如何进行的?
假设有一个含10000 个记录的文件,首先通过10 次内部排序得到10 个初始归并段R1~R10 ,其中每一段都含1000 个记录。然后对它们作如图10.11 所示的两两归并,直至得到一个有序文件为止 如下图
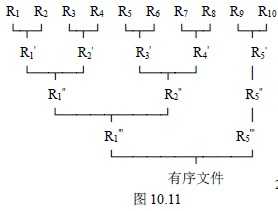
三 败者树
归并的方式最容易想到的是两路归并。
将40个文件编号1-40,1和2归并,3和4归并...39和40归并,生成了20个文件,再将这20个文件继续两路归并。
从40个文件变成20个文件,相当于把所有10G的数据从磁盘读出,再写到磁盘上,从20个文件到10个文件,也相当于把10G的数据从磁盘读出,再写到磁盘上。这种磁盘IO操作一共要执行6次。(2^6=64>40)
再来考虑K路归并。所谓K路归并,就是一次比较K路数据,选出最小的。例如当K=10,则是将40个文件分成1-10,11-20,21-30,31-40。对1-10,由于已序,故只要比较出这10个文件的第一个数,看哪个最小,哪个就写到新文件,再进行下一轮的比较。这样,只要2次磁盘IO就可以了。
假设我们将文件分为m份,使用K路归并,则磁盘IO的次数就是log K底m。我们当然是希望这个值越小越好。但是是不是K越大就越好呢?我们来看看算法的时间复杂度。
对于总共s个数据的K路归并,每次需比较K-1次,才能得出结果中的一个数据,s个数据就需要比较(s-1)(K-1)次
对于总共n个数据,分为m份,使用K路归并,总共需要比较 (log K底m) * (n-1)(K-1)= (logm/logK)*(n-1)(K-1) = logm*(n-1)*(K-1)/logK,当K增大时,(K-1)/logK是增大的,也即时间复杂度是上升的。因此要么K不能太大,要么找出一个新的方法,使得每次不用比较K-1次才得出结果中的一个数据。我们选择后者,由此引出了败者树。
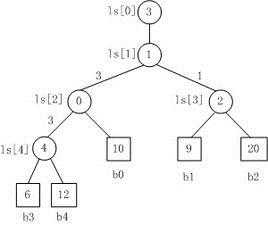
败者树实际上是一棵完全二叉树,败者树重构过程如下:
标签:数据交换 blank 选择 10g 一个 aik tar 外部排序 归并
原文地址:https://www.cnblogs.com/carrothhh/p/10765755.html