查找和排序-8.希尔排序

标签：时间   性能   排序   ima   实现   print   图片   轻松   数学   

希尔排序
（1）希尔排序（shell sort）这个排序方法又称为缩小增量排序，是1959年D·L·Shell提出来的。该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。
（2）由于开始时，increment的取值较大，每个子序列中的元素较少，排序速度较快，到排序后期increment取值逐渐变小，子序列中元素个数逐渐增多，但由于前面工作的基础，大多数元素已经基本有序，所以排序速度仍然很快。
（3）希尔排序举例：

1>下面给出一个数据列：

2>第一趟取increment的方法是：n/3向下取整+1=3（关于increment的取法之后会有介绍）。将整个数据列划分为间隔为3的3个子序列，然后对每一个子序列执行直接插入排序，相当于对整个序列执行了部分排序调整。图解如下：

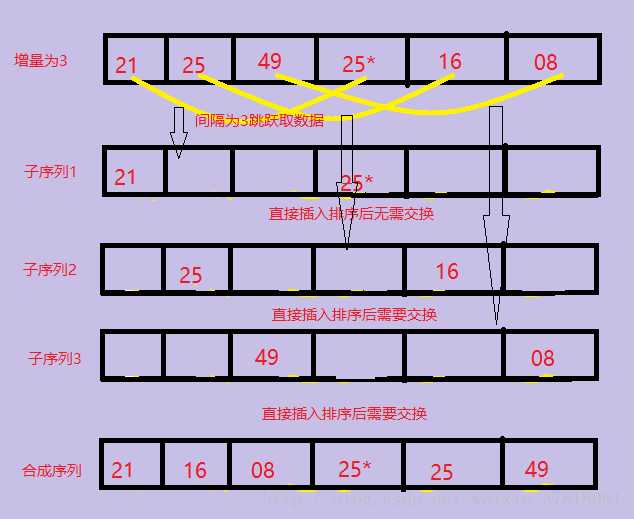
3>第二趟将间隔increment= increment/3向下取整+1=2，将整个元素序列划分为2个间隔为2的子序列，分别进行排序。图解如下：

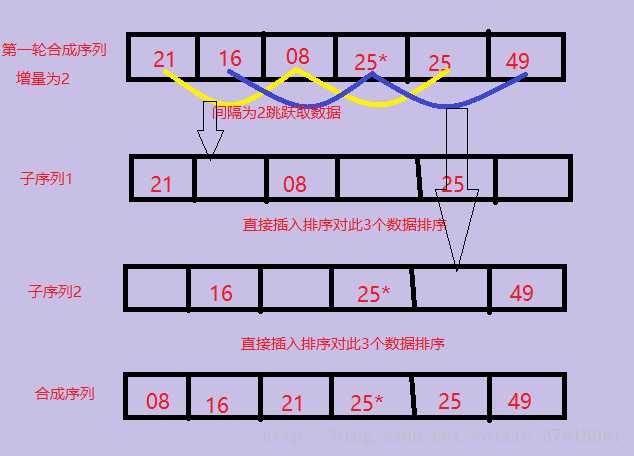
4>第3趟把间隔缩小为increment= increment/3向下取整+1=1，当增量为1的时候，实际上就是把整个数列作为一个子序列进行插入排序，图解如下：

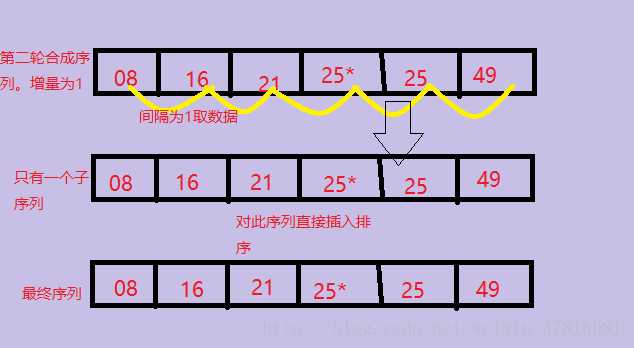
5>直到increment=1时，就是对整个数列做最后一次调整，因为前面的序列调整已经使得整个序列部分有序，所以最后一次调整也变得十分轻松，这也是希尔排序性能优越的体现。

算法实现

def insert_sort_gap(li,gap): 
    for i in range(gap,len(li)):#3-4
        tmp = li[i]         
        j = i-gap           
        while j >= 0 and li[j] > tmp :    
            li[i] = li[j]        
            j-=gap                 
        li[j+gap]=tmp   

def shell_sort(li):
    d = len(li)//2
    while d>=1:
        insert_sort_gap(li,d)
        d //= 2

li = [8,7,4,6,1,2,3,5]
print(li)
shell_sort(li)

关于希尔排序的性能分析

（1）对希尔排序的时间复杂度分析很困难，在特定情况下可以准确的估算排序码的比较次数和元素移动的次数，但要想弄清楚排序码比较次数和元素移动次数与增量选择之间的依赖关系，并给出完整的数学分析，还没有人能够做到。
（2）这里我们把3种常用的插入排序做一个程序测试，通过每种算法测试所执行的时间，来定性的认识希尔排序的性能优劣。测试的思路是通过生成1000个1——1000之间的随机数，令三种排序算法分别对其进行排序，输出排序所花费的时间。

查找和排序-8.希尔排序

标签：时间   性能   排序   ima   实现   print   图片   轻松   数学   

原文地址：https://www.cnblogs.com/sunny666/p/10775581.html