标签：概念 线性 第一个 有限域 级别 设计 技术 轻松 多参数
目录
论文地址：http://ai2-website.s3.amazonaws.com/publications/XNOR-Net.pdf
??我们提出了两种标准卷积神经网络有效近似方法：二值化权值网络和XNOR网络。在二值化权值网络中，卷积核使用二值化进行近似，从而节省了32倍的内存。在XNOR网络中，卷积核和卷积层的输入都是二进制的， XNOR网络主要使用二进制运算来近似卷积。卷积运算速度提高58倍（就高精度运算的数量而言）和节省32倍内存。 XNOR网络提供了在CPU（而不是GPU）上实时运行最先进网络的可能性。我们的二进制网络简单，准确，高效，并且可以处理具有挑战性的视觉任务。我们在ImageNet分类任务评估方法。二值化权值版本的网络分类准确性AlexNet与全精度AlexNet相同。我们将我们的方法与最近的网络二值化方法BinaryConnect和BinaryNets进行比较，并且在ImageNet上以大幅度优于这些方法，在Top-1精度中超过16％。我们的开源代码位于：http://allenai.org/plato/xnornet
??深度神经网络（DNN）已经在包括计算机视觉和语音识别在内的多个应用领域中展现了突出的进步。在计算机视觉中，一种特殊类型的DNN，称为卷积神经网络（CNN），已经在物体识别[1,2,3,4]和检测[5,6,7]中展示了最先进的结果。
??卷积神经网络在目标识别和检测方面显示出可靠的结果，这些结果在现实世界是有用的。在最近的认可进展的同时，虚拟现实中也出现了有趣的进步（VR byOculus）[8]，增强现实（AR byHoloLens）[9]，以及智能可穿戴设备。将这两个部分组合在一起，我们认为现在正是为智能便携式设备配备最先进识别系统强大功能的最佳时机。然而，基于CNN的识别系统需要大量的存储容量和计算能力。虽然它们在昂贵的基于GPU的机器上表现良好，但它们通常不适用于手机和嵌入式电子产品等小型设备。
??例如，AlexNet [1]具有61M参数(占249MB内存)，对一个图像进行分类需要执行1.5B次高精度操作。对于更深的CNN，这些数字甚至更高，例如VGG [2]（参见4.1节）。这些模型很快就超过了像手机这样的小型设备的有限存储，电池电量和计算能力。
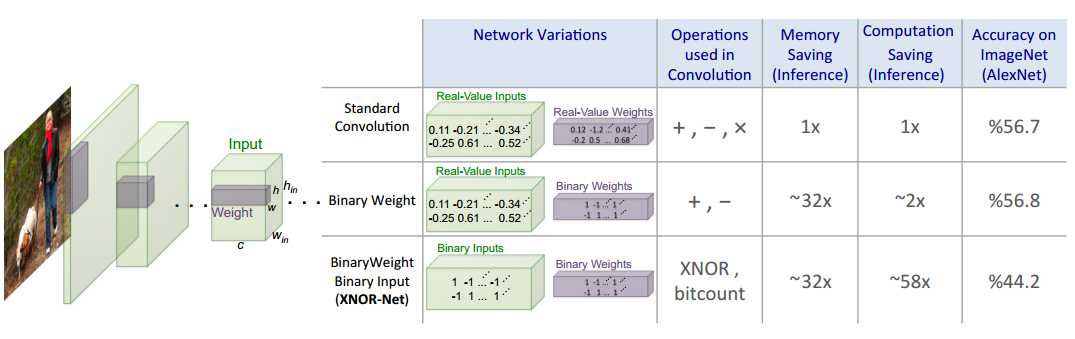
图1：我们提出了卷积神经网络的两种有效变化。 二值化网络，卷积核权值为二进制值。 XNOR网络，权值和输入都是二进制值。 这些网络在存储和计算方面非常有效，而在自然图像分类方面非常准确。 这提供了在具有有限资源的便携式设备中使用精确视觉技术的可能性。
??在本文中，我们通过二值化权值引入一个简单，有效和准确的CNN近似，甚至对中间输入也二值化。我们的二值化方法旨在使用二进制卷积运算找到最佳近似值。我们证明了我们的神经网络二值化方法在ImageNet分类数字与标准全精度网络精确率相当，同时需要更少的内存和更少的浮点运算。
??我们研究了两个近似值：具有二值化权值的神经网络和XNOR网络。在二值化权值网络中，所有权重值都用二进制值近似。具有二进制权重的卷积神经网络比具有单精度权重值的等效网络小得多（~32×）。此外，当权重值是二进制时，可以仅通过加法和减法（没有乘法）来计算卷积，从而产生约2×加速效果。大型CNN的二进制加权近似可以兼容小型便携式设备的存储容量，同时保持相同的精度水平（见第4.1节和第4.2节）
??为了进一步理解这个想法，我们引入了XNOR网络，其中卷积和全连接层的权重和输入都用二值化值近似。 二值化权值和输入可以实现有效卷积运算。 如果卷积的所有操作数都是二进制的，那么可以通过XNOR和位运算操作来估算卷积[11]。 XNOR网络可以精确逼近CNN，同时在CPU中提供约58倍的加速效果（就高精度操作的数量而言）。 这意味着XNOR-Nets可以在具有小内存且没有GPU的设备中实现实时运算（XNOR网络中的前向传播可以在CPU上非常有效地完成）。
??据我们所知，本文是第一次尝试在ImageNet等大型数据集上对二元神经网络进行评估。 我们的实验结果表明，我们提出的卷积神经网络二值化方法大大优于[11]最先进的网络二值化方法，达到了ImageNet挑战ILSVRC 2012中的Top1图像分类准确率（16.3％）。我们的贡献有两方面：首先，我们引入了一种在卷积神经网络中对权值进行二值化的新方法，并展示了我们与最先进的解决方案相比的优势。 其次，我们介绍了XNOR网络，一种深度神经网络具有二进制权重和二进制输入的模型表明，与标准网络相比，XNOR-Nets可以获得类似的分类精度度，同时效率明显更高。
??深度神经网络经常在其模型中遭受过多参数化和大量冗余的问题。 这通常会导致计算和内存使用效率低下[12]。 已经提出了几种方法来解决深度神经网络中有效的训练和前向传播。
??Shallow networks ：使用较浅的模型来近似深度神经网络可以减小网络的大小。 Cybenko的早期理论工作表明，具有足够大的单个隐藏的sigmoid单元层的网络可以逼近任何决策边界[13]。然而，在几个领域（例如，视觉和语音），浅网络不能与深模型竞争[14]。 [15]训练SIFT特征上的浅网络对ImageNet数据集进行分类。他们表明很难训练具有大量参数的浅网络。 [16]提供了关于小型数据集（例如，CIFAR-10）的经验证据，即浅网络能够学习与深层相同的功能。为了获得类似的精度，浅网络中的参数数量必须接近深度网络中的参数数量。他们通过首先训练最先进的深层模型，然后训练浅模型来模拟深层模型来做到这一点。这些方法与我们的方法不同，因为我们使用的方法标准深层架构不是浅层结构。
??Compressing pre-trained deep networks(重点) ：在先前训练的网络中修剪冗余的，无信息的权值，在前向传播时减少了网络的大小。权值衰减[17]是修剪网络的早期方法。Optimal Brain Damage [18]和Optimal Brain Surgeon [19]使用Hessian的损失函数来实现通过减少连接数来修剪网络。最近[20]在几个现有技术的神经网络中将参数的数量修剪了一个数量级。 [21]提出减少的激活值的数量来压缩和加速。深度压缩[22]减少了在大型网络上进行前向传播所需的存储容量和计算量，因此可以将它们部署在移动设备上。它们删除冗余连接并量化权重，以便多个连接共享相同的权重，然后他们使用霍夫曼编码来压缩权重。 HashedNets [23]使用哈希函数通过随机分组权重来减小模型大小，这样哈希桶中的连接使用单个参数值。矩阵分解已被[24,25]使用。我们与这些方法不同，因为我们不使用一个预训练网络。我们从头开始训练二值化网络。
??Designing compact layers：在深层网络的每一层设计紧凑块可以帮助节省内存和计算成本。 在网络架构[26]，GoogLenet [3]和Residual-Net [4]中用全局平均池化替换全连接层，在几个基准测试中获得了最先进的结果。 已经提出了Residual-Net [4]的瓶颈结构来减少参数的数量并提高速度。 在[27]中分解3×3的卷积核为2个1×1的卷积核，并且在目标识别方面产生了最先进的性能。 1×1卷积核代替3×3卷积可以[28]创建一个非常紧凑的神经网络，可以在获得高精度的同时实现约50倍的参数数量减少。 我们的方法与这项工作不同，因为我们使用完整的网络（不是紧凑版本），且使用二值化参数。
??Quantizing parameters：高精度参数对于在深度网络中实现高性能不是非常重要。 [29]提出通过矢量量化技术量化DNN中全连接层权重。他们表现得很好将权重值阈值化为零只会使ILSVRC2012的Top1精度降低10％。 [30]提出了一种可证实的多项式时间算法，用于训练具有+ 1/0 / -1权重的稀疏网络。在[31]中将8位整数的定点实现与32位浮点激活值进行了比较。[32]提出了另一个具有三值化权重和3比特位激活值的定点值网络。在[33]中最小化L2误差来量化网络可以对MNIST和CIFAR-100数据集实现更高的准确度。 [34]提出在反向传播过程量化网络每层的输出。为了将一些剩余的乘法转换成二进制移位，神经元限制为2的整数次幂。在[34]中，它们在测试阶段保留全精度权重，并且仅在反向传播过程中量化神经元，而不是在前向传播期间量化。因为我们正在量化网络中的参数，所以工作类似于这些方法。但是我们的量化是极端情况+ 1，-1。
??Network binarization：这些工作与我们的方法最相关。有几种方法试图对神经网络中的权重和激活进行二值化。由于二进制量化的破坏性，高度量化网络（例如二值化）的性能被认为非常差[35]。 [36]中的期望BackPropagation（EBP）表明，具有二值化权重和激活值的网络可以实现高性能。这是通过变分贝叶斯方法完成的，该方法用二进制权重和神经元推断网络。在[37]中提出了一种类似于EBP的方法，运行全二值化娿的网络，显示出效果显着提高。在EBP中，二值化参数仅在前向传播期间使用。 BinaryConnect [38]扩展了EBP背后的概率思想。与我们的方法类似，BinaryConnect使用权重的实值版本作为二值化过程的关键参考。通过简单地忽略更新中的二值化，使用反向传播的误差更新实值权重。 BinaryConnect在小数据集（例如，CIFAR-10，SVHN）上实现了不错的结果。我们的实验表明，这种方法在大规模数据集（例如ImageNet）上并不是很成功。 BinaryNet [11]建议扩展了BinaryConnect，其中权重和激活值都是二值化的。我们的方法在二值化方法和网络结构上与它们不同。我们还将我们的方法与ImageNet上的BinaryNet进行了比较，我们的方法在很大程度上优于BinaryNet。[39]声称权值二值化引入的噪声提供了一种正规化形式，可以帮助提高测试精度。此方法将权重二值化，同时保留全精度的激活值。 [40]提出了一系列具有随机输入的机器进行完全二值化训练和测试。 [41]用二进制权值和输入重新训练先前训练好的神经网络。
??我们用三元组<I,W,*****>代表L层CNN架构，I是一组张量，其中每个元素I = Il(l=1,..L)是第l层CNN的输入张量（图1中的绿色立方体）。W是一组张量，其中该集合中的每个元素W = Wlk(k = 1,,, K1）是CNN的第l层中的第k个权值卷积核。Kl是CNN的第l层中的权值卷积核的数量。*表示卷积操作，I和W作为它的操作数。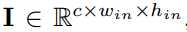
，其中（c,win,hin)分别表示通道，宽度，高度。
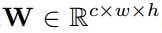
，其中w<=win,h<=hin。我们提出二进制CNN的两种变体：二值化权重，其中W的元素是二进制张量和XNOR网络，其中I和W的元素都是二值化张量。
??为了限制卷积神经网络<I,W,*****>具有二值化权重，我们使用二进制卷积核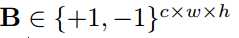
近似实值权重卷积核W∈W; 通过缩放比例α∈R +使得W≈αB。 卷积操作可以通过以下方式近似：
??其中，⊕表示没有任何乘法的卷积。 由于权值是二值化的，我们可以通过加法和减法来实现卷积。 与单精度卷积相比，二值化的权值卷积核可减少约32倍内存使用量。 我们用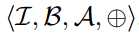
表示具有二值化权重的CNN，其中B是一组二进制张量，A是一组正实数标量，B = Blk是二值化卷积核，α= Alk是比例因子，Wlk≈AlkBlk
??估计二值权重：在不失一般性的情况下，我们假设W，B是Rn中的向量，其中n = c×w×h。 为了找到W≈αB的最佳估计，我们解决了以下优化：
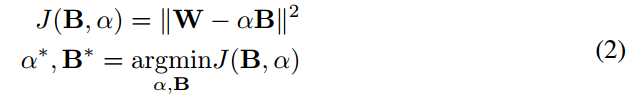
通过扩展等式2，我们得到了:
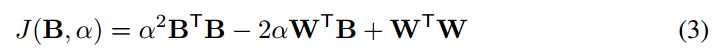
因为B∈{+1，-1}n,BTB = n是一个常数。WTW也是常数，因为W是已知变量。 让我们定义c = WTW。 现在，我们可以重写等式3如下：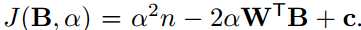
。 B的最优解可以通过最大化以下约束优化来实现:(注意α是正值在等式2中，因此在最大化中可以忽略）
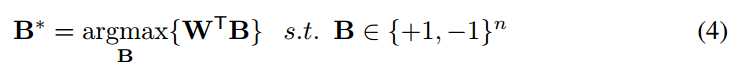
如果Wi≥0则指定Bi = +1并且如果Wi <0则指定Bi = -1，则可以解决该优化，因此最优解是B* = sign(W)。 为了找到比例因子α*的最优值，我们采用J的导数相对于α并将其设置为零：
用sign(W)代替B*：
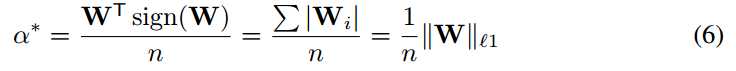
因此，通过取权值的符号符号函数值可以简单地实现二元权重卷积核的最佳估计。 最佳比例因子是绝对权重值的平均值。
??训练二元权值网络：训练CNN的每次迭代都涉及三个步骤; 正向传播，反向传播和参数更新。为了训练具有二值化权重的CNN（在卷积层中），我们仅在前向传播和反向传播期间对权重进行二值化。为了计算符号函数sign(r)的梯度，我们采用与[11]相同的方法，其中
。 在缩放符号函数之后的反向传播的梯度是
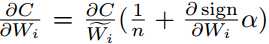。 为了更新参数，我们使用高精度（实值）权重。 因为，在梯度下降中参数变化很小，更新参数后的二值化忽略了这些变化，无法改善训练目标。 [11,38]也采用这种策略来训练二进制网络。
??算法1演示了我们训练具有二值化权重的CNN的过程。首先，我们通过计算B和A对每层的权重卷积核进行二值化。然后我们使用二值化权重及其相应的缩放因子来调用前向传播，其中所有卷积操作都按等式1执行， 然后，我们调用反向传播，其中估算的权重卷积核W用来计算梯度。 最后，参数和学习速率通过更新规则更新，例如，带动量的SGD更新或ADAM [42]。
??训练结束后，无需保留实际权重。 因为，在验证时，我们仅使用二值化权重执行前向传播。
??到目前为止，我们设法找到二值权重和比例因子来估计实际值权重。卷积层的输入仍然是实值张量。现在，我们解释如何二值化权重和输入，可以使用XNOR和位计数操作有效地实现卷积运算。这是我们的XNOR网络的关键因素。为了约束卷积神经网络<I,W,*>有二值化权重和输入，我们需要在卷积运算的每一步强制执行二值化操作。卷积包括重复移位操作和点积。移位运算时在输入上移动权重卷积核，权重卷积核的值和输入的相应部分之间执行逐元素乘法。如果我们用二进制运算表示点积，则可以使用二进制运算来近似卷积。两个二元向量之间的点积可以通过XNOR-Bitcounting操作来实现[11]。在本节中，我们将解释如何通过两个{+1,-1}n向量之间的点积来近似Rn中两个向量之间的点积。接下来，我们演示如何使用此近似来估计两个张量之间的卷积运算。
Binary Dot Product: 为近似X，W∈Rn之间的点积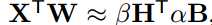
,其中H，B∈{+1,-1}n，我们主要解决下面的优化函数：
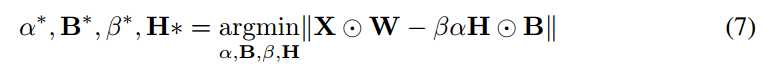
其中○表示元素乘积。我们定义Yi = XiWi 其中Y∈Rn，Ci = HiBi C∈{+1,-1}n ,并且γ = βα ，等式7可以写成如下：
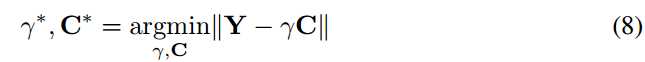
最佳解可以从等式2推出，如下所示：
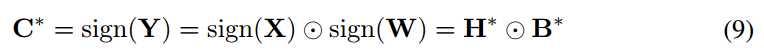
因为|Xi|,|Wi |是独立的，已知Yi = XiWi 然后
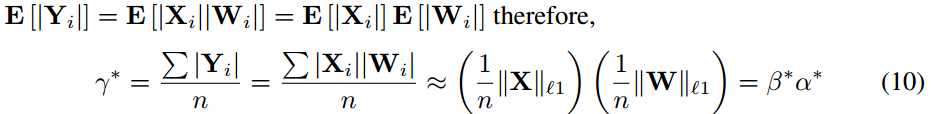
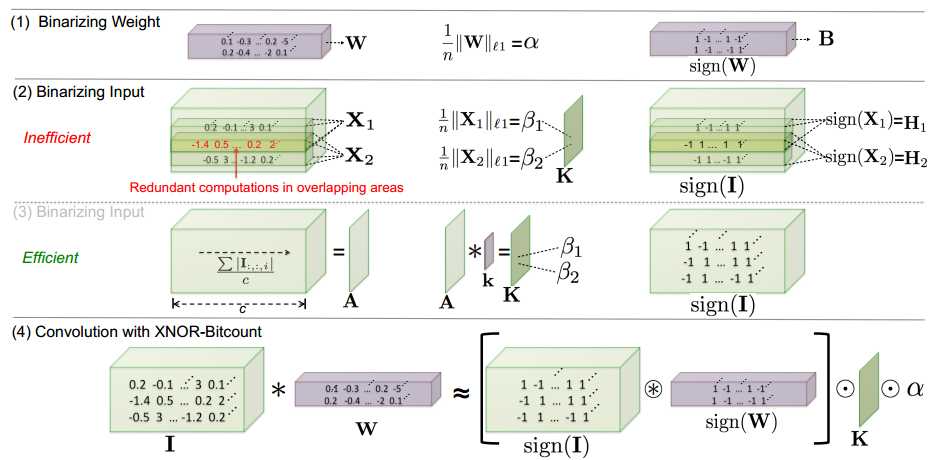
Binary Convolution: 带有输入向量
的卷积核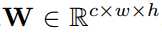
(其中win >> w, hin >>h)需要为所有在I与W相同大小的子张量计算缩放因子β。这些子张量中的两个在图2（第二行）中由X1和X2示出。 由于子向量之间的重叠，计算所有可能的子张量的β会导致大量的冗余计算。为了克服这种冗余，首先，我们计算一个矩阵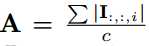
，这是通道中输入I中元素的绝对值的平均值。然后我们用一个2D 过滤器k∈Rwxh和A卷积，K = A*k，其中对于任意ij, 都有kij = 1/wxh。K包含在输入I中所有子向量的缩放因子β。Kij对应以位置ij为中心的子张量（横跨宽度和高度）。 这个过程在图2的第三行中示出。一旦我们获得了I的所有权重和子张量的缩放因子α，β（用K表示），我们可以近似估算输入I和权重卷积核W之间的卷积。 使用二进制操作：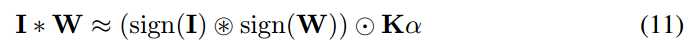
其中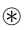
表示使用XNOR和bitcount操作的卷积操作。 这在图2的最后一行中说明。请注意，与二进制操作相比，非二进制操作的数量非常少。
训练XNOR网络：CNN中的典型块结构包含几个不同的层。图3（左）说明了CNN中的典型块结构。该块具有以下顺序的四个层：1-卷积，2-批量标准化，3-激活和4-池化层。批量标准化层[43]通过其均值和方差对输入批次进行标准化。激活是元素方式的非线性函数（例如，Sigmoid，ReLU）。池化层在输入批次上应用任何类型的池化（例如，最大值，最小值或平均值）。在二值化输入上应用池化会导致重要信息丢失。例如，二进制输入上的max-pooling返回一个张量，它的大部分元素都等于+1。因此，我们将池化总层放在卷积之后。为了进一步减少二值化导致的信息丢失，我们在二值化之前对输入进行标准化。这确保了数据分布均值保持为零，因此，在零处的阈值处理会减少的量化误差。二进制CNN块中的层顺序如图3（右）所示。
??如3.2节所述，二进制激活层（BinActiv）计算K和符号函数（I）。在下一层（BinConv）中，给定K和符号（I），我们通过等式11计算二进制卷积。然后在最后一层（池化层），我们应用池化操作。我们可以在二值化卷积之后插入非二值化激活函数（例如，ReLU）。当我们使用最先进的网络时（例如，AlexNet或VGG），这十分有帮助时。
??一旦我们具有二进制CNN结构，训练算法将与算法1相同
??二进制梯度：每层反向传递中的计算瓶颈是计算权重卷积核（w）和相对于输入（gin）的梯度之间的卷积。 与前向传播中的二值化类似，我们可以在反向传播时二值化gin。 使用二值化计算将产生非常有效的训练过程。 注意，如果我们使用等式6来计算gin的缩放因子，则SGD的最大变化方向将会消失。 为了保持所有维度的最大变化，我们使用maxin（|gini|）作为缩放因子。
??k位量化：到目前为止，我们使用sign（x）函数对权重和输入进行1位量化。 通过使用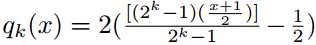
而不是符号函数，可以容易地将量化级别扩展到k位。 其中[.]表示舍入运算，x ∈[-1，1]。
??我们通过分析其效率和准确性来评估我们的方法。我们通过计算由二进制卷积与标准卷积实现的计算加速（就高精度计算的数量方面）来测量效率。为了测量准确度，我们在大型ImageNet数据集上执行图像分类。本文是第一篇在二值化神经网络评估ImageNet数据集的工作。我们的二值化技术是通用的，我们可以使用任何CNN架构。我们在实验中评估了AlexNet [1]和两个更深层次的架构。我们比较一下最近两篇关于神经网络二值化的研究方法; BinaryConnect [38]和BinaryNet [11]。我们的二值化权值网络AlexNet的分类准确性与AlexNet的全精度版本一样准确。这种分类精度大大优于二值化神经网络上的竞争对手。我们还提出了一项消融研究，评估了我们提出的方法的关键要素;计算缩放因子和二进制CNN的块结构。我们表明计算比例因子的方法对于达到高精度非常重要。
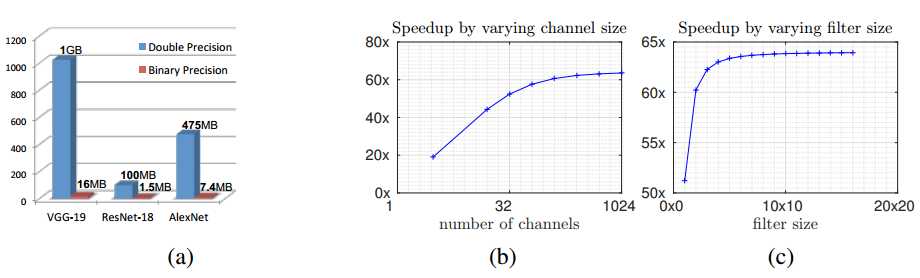
图4：该图显示了二进制卷积在存储器（a）和计算方面（b-c）的效率比较。 (a)在三种不同的架构（AlexNet，ResNet-18和VGG-19）中对比二值化和双精度权重所需的内存大小。 （b，c）显示在(b)不同数量的通道和卷积核大小下的二进制卷积获得的加速情况(c)
??在标准卷积中，计算操作总数是cNWNI，其中c是通道数，NW= wh，NI= winhin。 请注意，一些现代CPU可以将乘法和加法融合为单个周期操作。 在这些CPU上，BinaryWeight网络无法提供加速。 我们的卷积二进制近似
（等式11）具有cNWNI次二进制运算和NI次非二进制运算。 使用当前一代的CPU，我们可以在一个CPU时钟内执行64次二进制运算，因此可以通过计算加速比：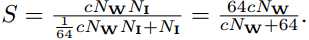
??加速取决于通道大小和卷积核大小，但不取决于输入大小。在图4-(b-c)中，我们通过改变通道数和卷积核大小来说明实现的加速效果。在更改一个参数时，我们固定其他参数如下：c = 256，nI = 14^2和nW = 3^2（ResNet [4]架构中的大多数卷积都有此结构体）。使用我们的近似卷积，获得了62.27倍的理论加速，但在我们的CPU实现中，所有开销，我们在一个卷积中实现了58倍的加速（不包括内存分配和内存访问的过程）。设置小通道尺寸（c = 3）和卷积核尺寸（NW = 1×1）的加速效果不是很好。这促使我们避免在CNN的第一层和最后一层进行二值化。在第一层中，chanel大小为3，在最后一层中，卷积核大小为1×1。在[11]中使用了类似的策略。图4-a显示了具有二进制和双精度权重的三种不同CNN架构（AlexNet，VGG-19，ResNet-18）所需的存储容量。二值化权重网络非常小，可以轻松安装到便携式设备中。 BinaryNet [11]与我们的方法具有相同的内存和计算效率。
在图4中，我们展示了二进制卷积的计算和内存成本分析。对BinaryNet和BinaryCon有同样的分析。我们方法的关键区别在于使用缩放因子，它不会改变效率的顺序，同时准确性的显着提高。
??我们在自然图像分类任务中评估提出的方法的表现。到目前为止，在文献中，二元神经网络方法已经对有限域或简化数据集（例如CIFAR-10，MNIST，SVHN）进行了评估。为了与最先进的视觉进行比较，我们在ImageNet（ILSVRC2012）评估了我们的方法。 ImageNet拥有来自1K类别和50K验证图像的~1.2M列车图像。与具有相对较小图像的CIFAR和MNIST数据集相比，该数据集中的图像是具有相当高分辨率的自然图像。我们使用Top-1和Top-5精度报告我们的分类性能。我们采用三种不同的CNN架构作为二值化的基础架构：AlexNet [1]，残余网络（称为ResNet）[4]，以及GoogLenet [3]的变体。我们将二进制权重网络（BWN）BinaryConnect（BC）[38]和我们的XNOR-Networks（XNOR-Net）与BinaryNeuralNet（BNN）[11]进行比较。BinaryConnect（BC）是一种在前向和后向传播期间训练具有二值化权重的深度神经网络的方法。与我们的方法类似，它们在更新参数步骤期间保持实际权重值。我们的二值化与BC不同。 BC中的二值化可以是确定性的也可以是随机的。我们在比较中使用BC的确定性二值化，因为随机二值化效率不高。 [11]中使用和讨论了相同的评估设置。
??BinaryNeuralNet（BNN）[11]是一种神经网络，在训练中的前向传播和梯度计算过程中具有二值化权值和激活值。从概念上讲，这是与我们的XNOR网络类似的方法，但BNN中的二值化方法和网络结构与我们的不同。他们的训练算法类似于BC，他们在评估中使用确定性二值化。
??CIFAR-10：BC和BNN在CIFAR-10，MNIST和SVHN数据集上表现出近乎最先进的性能。 CIFAR-10上的BWN和XNOR-Net使用与BC和BNN相同的网络架构，错误率分别为9.88％和10.17％。 在本文中，我们探索了在更大，更具挑战性的数据集（ImageNet）上获得近乎最先进结果的可能性。
??AlexNet：[1]是一个有5个卷积层和2个全连接的层CNN架构。 这种架构是第一个在ImageNet分类任务上取得成功的CNN架构。 该网络有61M参数。 我们使用带有批标准化层的AlexNet[43]。
??训练：在每次训练迭代中，图像被调整大小以在其较小维度上具有256个像素，然后选择224×224的随机裁剪用于训练。 我们运行训练算法16个epoch，批量大小为512。我们在输出的soft-max上使用负对数似然作为我们的分类损失函数。 我们不使用本地响应规范化（LRN）层来实现AlexNet。 我们使用momentum=0.9的SGD来更新BWN和BC中的参数。 对于XNOR-Net和BNN，我们使用ADAM [42]。 ADAM收敛速度更快，通常可以实现二进制输入的更高精度[11]。 学习率从0.1开始，我们每4个epoch应用学习衰减速率=0.01。
??测试：在前向传播时，我们使用中心裁剪的224×224输入图片进行前向传播。
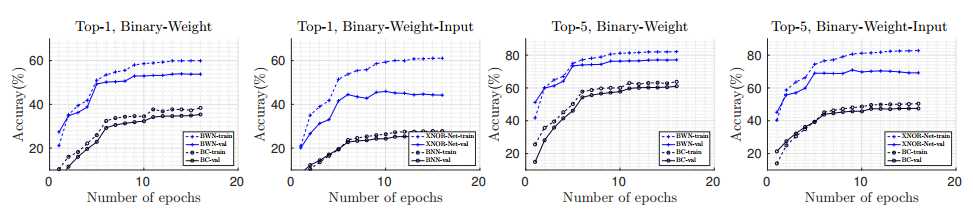
图5展示了Top-1和Top-5分的训练时期的训练和推理的分类准确性。 虚线表示训练精度，实线表示验证准确度。 在所有时代中，我们的方法比BC和BNN大得多（约17％）。 表1将我们的最终准确度与BC和BNN进行了比较。 我们发现权重（α）的缩放因子比输入（β）的缩放因子更有效。 去除β会使准确度降低一点（前1个亚历山大不到1％）。
二进制梯度：使用具有二进制梯度的XNOR-Net，top-1的精度将仅下降1.4％。
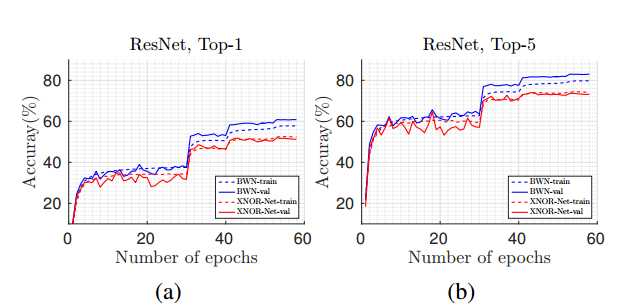
图6：该图显示了使用ResNet-18通过二值化权重网络和XNOR网络在ImageNet数据集上关于训练epoch的分类精度变化;（a）Top-1和（b）Top-1。
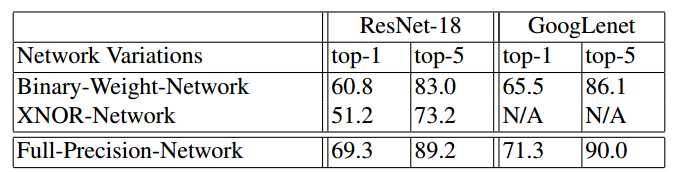
表2：该表比较了我们的二进制精度网络与ResNet-18和GoogLenet架构中的全精度网络实现的最终分类精度。
??Residual Net : 我们使用[4]中提出的ResNet-18 类似B的剪切版。
??训练：在每次训练迭代中，图像在较小维度上在256和480像素之间随机调整大小，然后选择224×224的随机裁剪进行训练。我们运行58个epoch的训练算法，批量大小等于256个图像。 学习率从0.1开始，我们分别在30个epoch和40epoch时使用0.01的学习率衰减。
??测试：在测试时，我们使用224×224的中心裁剪进行前向传播。
??图6展示了训练和测试沿epoch的分类准确性变化（Top-1和Top-5）。 虚线表示训练，实线表示测试。 表2显示了BWN和XNOR-Net的最终准确率。
??GoogLenet Variant : 我们尝试使用一个变种GoogLenet [3]做实验，它与原网络有相似数量的参数和连接，但只有简单的卷积，没有分支。 它有21个卷积层，卷积核大小在1×1和3×3之间交替。
??训练：在较小的维度上，图像在256和320像素之间随机调整大小，然后选择224×224的随机裁剪进行训练。 我们运行80个历元的训练算法，批量大小为128。学习率从0.1开始，我们使用多项式速率衰减，β= 4。
??测试：在测试时，我们使用224×224的中心裁剪。
??我们的方法与以前的网络二元化方法有两个主要区别; 二值化技术和我们二值化CNN中的块结构。
??对于二值化，我们在每次训练迭代中找到最佳比例因子。对于块结构，我们对块中的层进行排序以减少训练XNOR-Net的量化损失。在这里，我们评估每个元素在二值化网络性能中的影响。而不是使用等式6计算缩放因子α
，可以将α视为网络参数。换句话说，二值化卷积后的层将卷积的输出乘以每个卷积核的标量参数。这类似于在批量标准化中计算仿射参数。表3-a比较了两种计算缩放因子的方法下二值化网络的性能。正如我们在3.2节中提到的，CNN中的典型块结构不适合二值化。表3-b比较了标准块结构C-B-A-P（卷积，批量标准化，激活化，池化）与我们的结构B-A-C-P。（A，是二值化激活）
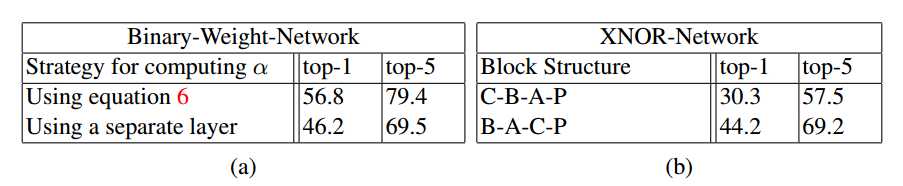
表3：在此表中，我们评估了我们方法的两个关键要素; 计算最佳缩放因子并为具有二进制输入的CNN块中的层指定正确的顺序。（a）证明了缩放因子在训练二元权重网络中的重要性，（b）表明我们在CNN块中对层进行排序的方式对于训练XNORNetworks至关重要。 C，B，A，P分别代表卷积，批标准化，激活函数（这里是二值激活）和池化。
??我们为神经网络引入一种简单，有效和准确的二进制近似。 我们训练一个神经网络，它可以学习找到权重的二进制值，这将网络的大小减少了大约32倍，并提供将非常深的神经网络加载到内存有限的便携式设备中的可能性。 我们还提出了一种架构XNOR-Net，它主要使用逐位运算来近似卷积。 这提供了约58倍的加速，并且使得能够实时地在CPU（而不是GPU）上运行最先进的深度神经网络。
本人根据谷歌翻译组织整理语句，英语水平有限，翻译错误望指正
论文翻译：XNOR-Net: ImageNet Classification Using BinaryConvolutional Neural Networks
标签：概念 线性 第一个 有限域 级别 设计 技术 轻松 多参数
原文地址：https://www.cnblogs.com/huxiaozhouzhou/p/10795177.html
