标签:矩阵 div bit lowbit \n info 需要 区间修改 cst
给定一个序列a,进行很多次操作:
访问a[l ~~ r]的区间和;
将a[i] 的值修改为 a[i] + k;
1 #include <cstdio> 2 #include <algorithm> 3 4 #define MAXN 2222 5 6 int n, m; 7 int a[MAXN], s[MAXN]; 8 9 int main() { 10 scanf("%d%d", &n, &m); 11 for(int i = 1; i <= n; i++) { 12 13 scanf("%d", &a[i]); 14 s[i] = s[i - 1] + a[i]; //前缀和 15 } 16 for(int i = 1, x, y; i <= m; i++) {//m次操作 17 scanf("%d%d", &x, &y); 18 printf("%d\n", s[y] - s[x - 1]);//s[y] - s[x - 1]即为x ~~ y的区间和 19 } 20 return 0; 21 } 22 /* 23 10 100 24 1 9 5 6 8 7 4 3 6 9 25 */
**/*树状数组:动态维护前缀和*/**
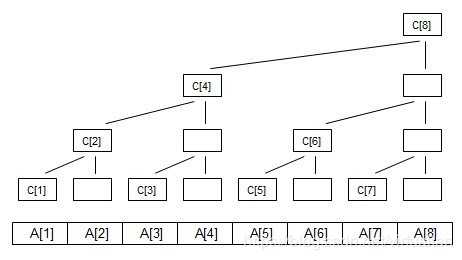
1 #include<cstdio> 2 3 #define lowbit(x) (x & -x) 4 #define MAX 11111 5 int n,m; 6 int t[MAX],a[MAX];//t为树状数组 7 8 void add(int x, int k) {//单点修改(向树上走) 9 for(int i = x; i <= n; i += lowbit(i)) { 10 t[i] += k; 11 } 12 } 13 14 int query(int x) {//区间查询(在树下向前推进)//求的是前缀和 15 int sum = 0; 16 for(int i = x; i; i -= lowbit(i)) { 17 sum += t[i]; 18 } 19 return sum; 20 } 21 22 void lineplus(const int & l , const int &r, const int &k) { 23 add(l , k); 24 add(r + 1 , -k); 25 } //区间加 & 单点查询 26 27 int main() { 28 scanf("%d%d",&n,&m); 29 for(int i = 1; i <= n; i++) { 30 scanf("%d",&a[i]); 31 add(i , a[i]); 32 } 33 int x,y; 34 /*for(int i = 1; i <= m; i++) { 35 scanf("%d%d",&x,&y); 36 printf("%d\n",query(y) - query(x - 1));//求的是区间和(x~~y) 37 }*/ 38 int k; 39 scanf("%d%d%d",&x,&y,&k); 40 lineplus(x,y,k);//x~~y区间加k 41 } 42 43 ``` 44 /* 45 5 100 46 1 4 5 6 3 47 1 48 ans:1 49 */
1 #include <cstdio> 2 #include <algorithm> 3 4 #define MAXN 222222 5 6 using namespace std; 7 8 int n, ans, tot; 9 int a[MAXN], b[MAXN], t[MAXN];//t为树状数组,b用来离散化a 10 11 int lowbit(int x) { 12 return x & -x; 13 } 14 15 int query(int x) { 16 int s = 0; 17 for(int i = x; i; i -= lowbit(i)) s += t[i]; 18 return s; 19 }//区间查询 返回的是前缀和 20 21 void add(int x) { 22 for(int i = x; i <= n; i += lowbit(i)) t[i]++; 23 } 24 25 int main() { 26 scanf("%d", &n); 27 for(int i = 1; i <= n; i++) scanf("%d", &a[i]), b[i] = a[i];//b用于去重 28 29 //离散化:将数值转化为排名,减小取值范围 30 sort(b + 1, b + 1 + n);//先升序排个序 31 tot = 1;//第一个是不用去重的 32 printf("去重前 "); 33 for(int i = 1; i <= n; i++) printf("%d ", b[i]);// 34 for(int i = 2; i <= n; i++) if(b[i] != b[tot]) b[++tot] = b[i];//去重 ,从第二个开始 35 //补:unique()函数是一个去重函数,功能是去除相邻的重复元素(只保留一个) 36 //unique(num,mun+n)返回的是num去重后的尾地址, 37 printf("\n去重后 "); 38 for(int i = 1; i <= tot; i++) printf("%d ", b[i]); 39 for(int i = 1; i <= n; i++) a[i] = lower_bound(b + 1, b + 1 + tot, a[i]) - b; 40 //lower_bound(b + 1, b + 1 + tot, a[i])是在区间b + 1~~~b + 1 + tot中找到第一个大于等于a[i]的数,并返回它的地址 41 //所以要“- b”减b ,之后,返回的是值等于a[i]的下标(即排名) 因为b一定有a[i] 所以它就是找第一个等于a[i]的数 42 printf("\n离散化a "); 43 for(int i = 1; i <= n; i++) printf("%d ", a[i]); 44 45 for(int i = 1; i <= n; i++) { 46 add(a[i]); 47 int tmp = query(a[i]); 48 tmp = i - tmp;//tmp一开始是i之前的 大于i的 数 的 个数 49 ans += tmp;//逆序对的个数的和 50 } 51 printf("\n%d\n", ans); 52 return 0; 53 } 54 55 ``` 56 57 /* 58 7 59 6 2 5 1 3 7 4 60 7 61 33 23 17 999 5 17 999 62 */
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 5 #define MAXN 1111 6 #define MAXM 1111 7 8 int n,m;//长&宽 9 int a[MAXN][MAXM],s[MAXN][MAXM]; 10 /*a为矩阵每个点的值,s[i][j]表示 以[i,j]为右下角的矩阵中(左上角为(0,0)) 11 所有方格中数的和 12 */ 13 int x1,y1,x2,y2; 14 /*询问的是以(x1,y1)为左上 以(x2,y2)为右下的矩阵中 15 所有方格中数的和 16 */ 17 18 int main() { 19 scanf("%d%d",&n,&m); 20 for(int i = 1; i <= n; i++) { 21 for(int j = 1; j <= m; j++) { 22 scanf("%d",&a[i][j]); 23 } 24 } 25 //初始化: 26 for(int i = 1; i <= n; i++) { 27 for(int j = 1; j <= m; j++) { 28 s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; 29 // (都是已知的) s[i - 1][j - 1]为重复加的 然后加上他自己 30 } 31 } 32 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 33 printf("%d",s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]); 34 // s[x1 - 1][y1 - 1] 重复减的 35 //温馨提示:画个矩阵呗 36 }
给定一个序列a(初值全为0)。有很多次操作:
将a[I ~~ j]的每个值加上k
询问a[x]的值
(实际上是区间修改,单点查询问题,不过可以用差分数组改成区间查询(求p[i]的前缀和)单点修改(修改p[l],p[r + 1]的值)
差分数组的前缀和即为原数组,修改同步
代码:
1 #include<cstdio> 2 /* 5 2 4 4 3 3 p:5 -3 -2 0 -1 */ 4 #define MAXN 1111 5 int n,m;//给定序列a的长度为n,m次操作 6 int a[MAXN],p[MAXN];//p 表示a中相邻元素的差 例:p[i] = a[i] - a[i - 1] 7 // 即差分 8 int l,r,k; 9 10 void add(int l, int r, int k) { //加k的区间是【l , r】 11 p[l] += k;//p受影响的只有l 和 r+1 因为a[r + 1]值不变,所以p[r + 2]不变 12 p[r + 1] -= k;//只需要修改p[l] 和 p[r + 1] 的值,然后求一个前缀和就行了 13 } 14 15 void get_a() { 16 for(int i = 1; i<= n; i++) { 17 a[i] = a[i - 1] + p[i];//相当于一维前缀和 18 } 19 } 20 21 int main() { 22 scanf("%d%d",&n,&m); 23 for(int i = 1; i <=m; i++) { 24 scanf("%d %d %d",&l,&r,&k); 25 add(l,r,k); 26 } 27 get_a(); 28 for(int i = 1; i <=n; i++) { 29 printf("%d ",a[i]); 30 } 31 }
标签:矩阵 div bit lowbit \n info 需要 区间修改 cst
原文地址:https://www.cnblogs.com/virtualtan/p/10801626.html