标签:析构 分析 中序遍历 const 二叉树的深度 set dash 测试结果 das
#include<stdlib.h> #include<stdio.h> #include"BiTreeNode.h" #include<iostream> using namespace std; template <class T> class BiTree { private: BiTreeNode<T> *root; //根结点指针 void Destroy(BiTreeNode<T>* &t); void InOrder(BiTreeNode<T> *&t, void (*Visit)(T item)); void PostOrder(BiTreeNode<T>* &t, void (*Visit)(T item)); public: BiTree(void):root(NULL){}; //构造函数 ~BiTree(void){}; //析构函数 void PreOrder(BiTreeNode<T>* &t, void (*Visit)(T item)); //构造二叉树 void MakeTree(const T item, BiTree<T> &left, BiTree<T> &right); void Destroy(void); //撤消二叉树 BiTreeNode<T> *getroot() { return root; } void PreOrder(void (*Visit)(T item)); //前序遍历 void InOrder(void (*Visit)(T item)); //中序遍历 void PostOrder(void (*Visit)(T item)); //后序遍历 BiTreeNode<T> *createbintree(); //前序遍历建立二叉树 int numofnode(BiTreeNode<T> *t); //二叉树结点个数 void showmid(BiTreeNode<T> *t); //按中序遍历所有子节点值 BiTreeNode<T> *LeverCreateTree(BiTreeNode<T> *tr);//按层次遍历-非递归创建二叉树 BiTreeNode<T> *GetTreeNode(const T item, BiTreeNode<T> *left=NULL, BiTreeNode<T> *right=NULL) { BiTreeNode<T> *p; p = new BiTreeNode<T> (item, left, right); return p; } int leafnode(BiTreeNode<T> *t); //二叉树叶子节点个数 };
template <class T> class BiTreeNode { public: BiTreeNode<T> *leftChild; //左子树指针 BiTreeNode<T> *rightChild; //右子树指针 T data; //数据域 //构造函数和析构函数 BiTreeNode():leftChild(NULL), rightChild(NULL){} BiTreeNode(T item, BiTreeNode<T> *left = NULL, BiTreeNode<T> *right = NULL): data(item), leftChild(left), rightChild(right){} ~BiTreeNode(){} BiTreeNode<T>* &Left(void) //注意返回值类型为指针的引用类型 {return leftChild;} BiTreeNode<T>* &Right(void) //注意返回值类型为指针的引用类型 {return rightChild;} BiTreeNode<T>* setleft(){} };
1) 先序递归遍历
template <class T> void BiTree<T>::PreOrder(BiTreeNode<T> *&t, void (*Visit)(T item)) //使用Visit(item)函数前序遍历二叉树t { if(t != NULL) { Visit(t->data); //根 PreOrder(t->Left(), Visit); //左子树 PreOrder(t->Right(), Visit); //右子树 } }
2) 中序递归遍历
template <class T> void BiTree<T>::InOrder(BiTreeNode<T> *&t, void (*Visit)(T item)) //使用Visit(item)函数中序遍历二叉树t { if(t != NULL) { InOrder(t->Left(), Visit); //左子树 Visit(t->data); //根 InOrder(t->Right(), Visit); //右子树 } }
3) 后序递归遍历
template <class T> void BiTree<T>::PostOrder(BiTreeNode<T> *&t, void (*Visit)(T item)) //使用Visit(item)函数后序遍历二叉树t { if(t != NULL) { PostOrder(t->Left(), Visit); //左子树 PostOrder(t->Right(), Visit); //右子树 Visit(t->data); //根 } }
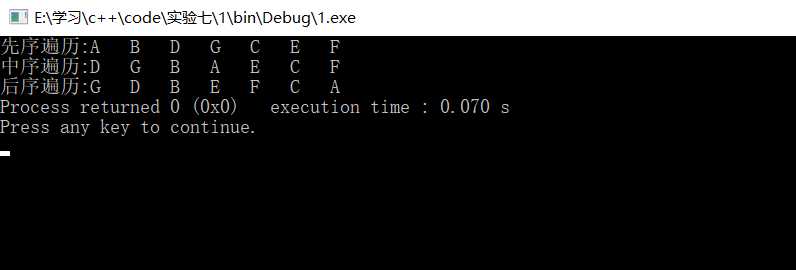
测试数据:
#include <iostream> #include<stdlib.h> #include"BiTree.h" using namespace std; template <class T> void Visit(T item) { cout << item << " "; } int main() { BiTree<char>a,b,c,d,e,f,g,null; g.MakeTree(‘G‘,null,null); d.MakeTree(‘D‘,null,g); b.MakeTree(‘B‘,d,null); e.MakeTree(‘E‘,null,null); f.MakeTree(‘F‘,null,null); c.MakeTree(‘C‘,e,f); a.MakeTree(‘A‘,b,c); cout<<"先序遍历:"; a.PreOrder(Visit); cout<<"\n中序遍历:"; a.InOrder(Visit); cout<<"\n后序遍历:"; a.PostOrder(Visit); return 0; }
结果:
template <class T> BiTreeNode<T> * BiTree<T>:: createbintree() { /*按照前序遍历的顺序建立一棵给定的二叉树*/ char ch; BiTreeNode<T> * t; if ((ch=getchar())==‘#‘) t=NULL; else { t = new BiTreeNode<T>; t->data=ch; t->leftChild=createbintree(); t->rightChild=createbintree(); } return t; } template <class T> void BiTree<T>::showmid(BiTreeNode<T> *t) { if(t!=NULL&&t->leftChild!=NULL) showmid(t->leftChild); cout<<t->data<<" "; if(t!=NULL&&t->rightChild!=NULL) showmid(t->rightChild); }
———— 其中增加showmid方法 显示给出结点下所有结点的值(按中序排列)
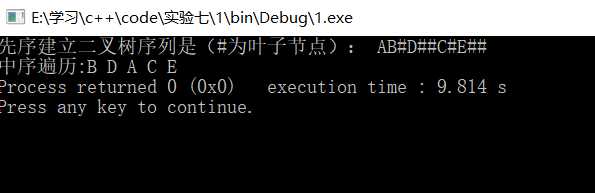
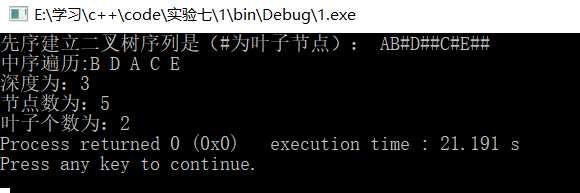
测试数据:
int main() { BiTree<char> a; cout<<"先序建立二叉树序列是(#为叶子节点): "; BiTreeNode<char> * b= a.createbintree(); cout<<"中序遍历:"; a.showmid(b); return 0; }
结果
template<class T> BiTreeNode<T> *BiTree<T>::LeverCreateTree(BiTreeNode<T> *tr)//按层次遍历-非递归创建二叉树 //输入序列:扩展结点度为2 { BiTreeNode<T> *q[10],*p,*k;//q为队列, int f=0,w=0,n=0;//f表示队头,w表示队尾。n为计数器 char ch; cin>>ch; if (ch==‘#‘||ch==‘@‘) tr=NULL;//空树时 else{//1 tr=new BiTreeNode<T>;//二叉树根结点的创建 tr->data=ch; tr->leftChild=NULL;//99 tr->rightChild=NULL;//99 q[w++]=tr; cin>>ch; while(ch!=‘@‘) { n=n%2; if (ch!=‘#‘) { p=new BiTreeNode<T>; p->data=ch; p->leftChild=NULL; p->rightChild=NULL; q[w++]=p; } else {p=NULL;} n++; if (n==1) {k=q[f];k->leftChild=p;} else if(n==2) {k=q[f++];k->rightChild=p;} cin>>ch; }//while }//1 return tr; }//LeverCreateTree
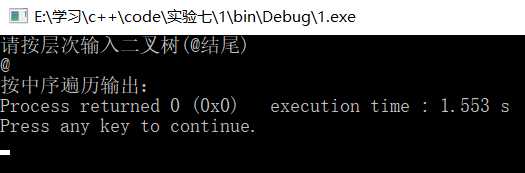
测试数据
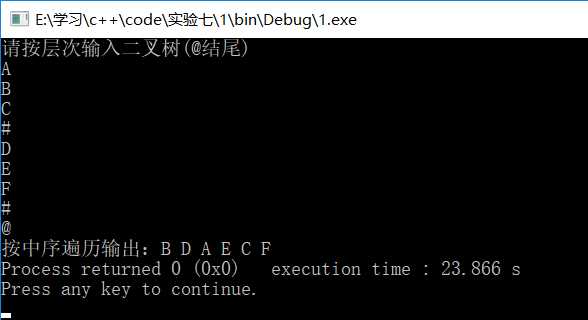
int main() { BiTree<char> A; BiTreeNode<char>* b; cout<<"请按层次输入二叉树(@结尾)"<<endl; BiTreeNode<char>* c=A.LeverCreateTree(b); cout<<"按中序遍历输出:"; A.showmid(c); return 0; }
结果:
1)空树
2)仅有一个结点树

3)一般的普通的二叉树
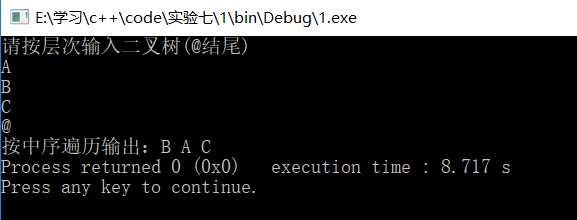
4)给出数据输入的序列。
去掉//99语句后:
理论上必须输入序列至少2层(1层即只有根结点)否则下方的左右子树不明确
但实际试验后没区别!!
template <class T> //二叉树的深度方法 int PostTreeDepth(BiTreeNode<T> *t) { int hl=0,hr=0; if (t==NULL) return 0; hl=PostTreeDepth(t->Left()); hr=PostTreeDepth(t->Right()); if (hl>hr) return (hl+1); else return (hr+1); }
template <class T> int BiTree<T>::numofnode(BiTreeNode<T> *t) //二叉树结点个数 { if (t==NULL) return 0; //递归出口 else return( numofnode(t->leftChild)+numofnode(t->rightChild) + 1); }
template <class T> int BiTree<T>::leafnode(BiTreeNode<T> *t)//二叉树叶子节点个数 { if(t==NULL) return 0; //递归出口 else if (t->leftChild==NULL && t->rightChild==NULL) return 1; //递归出口 else return(leafnode(t->leftChild)+leafnode(t->rightChild)); }
递归算法提示:
1)若T1和T2均为空,则返回值为1;
2)若T1和T2的深度均为1(即只有一个结点),则返回为1;
3)若T1的左子树和T2的左子树相似,并且T1的右子树和T2的右子树相似,则返回为1;
4)其它为返回值为0;
template <class T> int islike(BiTreeNode<T> * t1, BiTreeNode<T> * t2) { int t=0; if(t1==NULL && t2==NULL) t=1; else if(PostTreeDepth(t1)==PostTreeDepth(t2)&&PostTreeDepth(t1)==1) t=1; else if((islike(t1->leftChild,t2->leftChild)==1)&&(islike(t1->rightChild,t2->rightChild)==1)) t=1; else t=0; return t; }
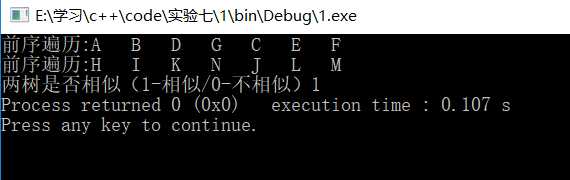
测试结果:
8
标签:析构 分析 中序遍历 const 二叉树的深度 set dash 测试结果 das
原文地址:https://www.cnblogs.com/cc123nice/p/10801717.html