标签:二叉树 下标 www. 出差 inline lowbit getch mod play
树状数组,顾名思义就是把一棵树型的数据存在数组中(运用在前缀和中)。
我们通过下面这图(图是百度百科找的)来理解它的原理和一些操作。(图中C是数组数组,A是1~n的数值)
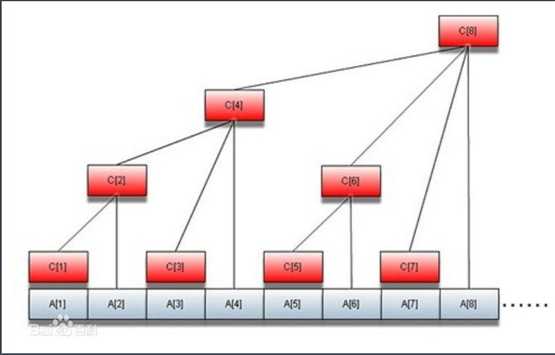
我们先看上面的那棵树,是不是看起来怪怪的,其实它就是个二叉树变形来的(不信你可以手动将它还原成我们平常树结构)。
接下来我们把树上的C数组存的值写一下:
C[ 1 ]=A[ 1 ]
C[ 2 ]=A[ 1 ]+A[ 2 ]
C[ 3 ]=A[ 3 ]
C[ 4 ]=A[ 1 ]+A[ 2 ]+A[ 3 ]+A[ 4 ]
C[ 5 ]=A[ 5 ]
C[ 6 ]=A[ 5 ]+A[ 6 ]
C[ 7 ]=A[ 7 ]
C[ 8 ]=A[ 1 ]+A[ 2 ]+A[ 3 ]+A[ 4 ]+A[ 5 ]+A[ 6 ]+A[ 7 ]+A[ 8 ]
由上面可得C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]。(k为i的二进制中从最低位到高位连续零的长度)
C数组存的值写好了,我们先来分析一下C数组与前缀和(sum[ ])之间的关系:
sum[ 1 ]=C[ 1 ]
sum[ 2 ]=C[ 2 ]
sum[ 3 ]=C[ 2 ]+C[ 3 ]
sum[ 4 ]=C[ 4 ]
sum[ 5 ]=C[ 4 ]+C[ 5 ]
sum[ 6 ]=C[ 4 ]+C[ 6 ]
sum[ 7 ]=C[ 4 ]+C[ 6]+C[ 7 ]
sum[ 8 ]=C[ 8 ]
可是我们又要怎么去运用这个关系来计算呢?这时候就要用到神奇的二进制了(不懂?没关系,一开始我也不懂,看下面就好了!)。
我们将数组下标都变成二进制:
sum[ 1 ]=C[ 1 ]
sum[ 10 ]=C[ 10 ]
sum[ 11 ]=C[ 10 ]+C[ 11 ]
sum[ 100 ]=C[ 100 ]
sum[ 101 ]=C[ 100 ]+C[ 101 ]
sum[ 110 ]=C[ 100 ]+C[ 110 ]
sum[ 111 ]=C[ 100 ]+C[ 110 ]+C[ 111 ]
sum[ 1000 ]=C[ 1000 ]
怎么样,现在看出了什么吗?
其实对它二进制的变化我们可以发现,其实计算sum[ 111 ]就是(C[ 111 ]+C[ (111-1)=110 ]+C[ (((111-1)=110)-10)=100 ]),到这其实就很明显了,其实就是( i - (i & -i))。
知识点:(这里的(i&-i)是取i的最低位1(-x是x的补码,举个例子10的8位二进制补码是00001010,-10的8位二进制补码是11110110,(两者取&就可以取到最低为1)=10,),不懂就百度一下吧))。
其实求c[ i ]也可以用到这个式子,把C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i],变一下就变成了C[i]=A[i-(i&-i)+1]+A[i-(i&-i)+2]+......A[i];
好了原理讲完了,剩下的看代码吧!
1:单点更新,区间查询
1 //模板题:https://www.luogu.org/recordnew/show/18606960 2 #include<iostream> 3 #include<cstdio> 4 #include<queue> 5 #include<string> 6 #include<string.h> 7 #include<set> 8 #include<stack> 9 #include<vector> 10 #include<algorithm> 11 #include<cmath> 12 #include<iterator> 13 #define mem(a,b) memset(a,b,sizeof(a)) 14 #define MOD 100000007 15 #define LL long long 16 #define INF 0x3f3f3f3f 17 const double pi = acos(-1.0); 18 const int Maxn=500010; 19 using namespace std; 20 inline int scan() 21 { 22 int x=0,c=1; 23 char ch=‘ ‘; 24 while((ch>‘9‘||ch<‘0‘)&&ch!=‘-‘)ch=getchar(); 25 while(ch==‘-‘)c*=-1,ch=getchar(); 26 while(ch<=‘9‘&&ch>=‘0‘)x=x*10+ch-‘0‘,ch=getchar(); 27 return x*c; 28 } 29 30 int gcd(int a,int b){ 31 return a==0?b:gcd(b%a,a); 32 } 33 int t[Maxn]; 34 int c[Maxn]; 35 int n,m; 36 int lowbit(int x){ 37 return x&-x; 38 } 39 void add(int i,int x){ 40 while(i<=n){ 41 c[i]+=x;///更新C数组 42 i+=lowbit(i); 43 } 44 } 45 int query(int i){ 46 int ans=0; 47 while(i>0){ 48 ans+=c[i];///求上面的sum 49 i-=lowbit(i); 50 } 51 return ans; 52 } 53 int main(){ 54 int a; 55 scanf("%d%d",&n,&m); 56 for(int i=1;i<=n;i++){ 57 scanf("%d",&a); 58 add(i,a);///将a加到第i个位置 59 } 60 int q,x,y; 61 while(m--){ 62 scanf("%d%d%d",&q,&x,&y); 63 if(q==1){ 64 add(x,y);///将y加到第x个位置 65 }else{ 66 printf("%d\n",query(y)-query(x-1));///询问xy区间和 67 } 68 } 69 return 0; 70 }
从上面的题目也可以看出,如果用简单的前缀和,那么更改操作复杂度肯定要爆炸
2:区间更新,单点查询。
区间更新要运用到差分思想。
如数组:2 4 5 3 6 8
它的差分数组为:2 2 1 -2 3 2
那我们把【2,4】上的数加1,那差分数组就变成了2 3 1 -2 2 2;可以看出只有第2个和第5个数变了,所以我们用树状数组维护差分数组,进行更改时只需要更改第2个和第5个就好了。
询问时就只要输出差分前缀和就好了(设c[i]=a[i]-a[i-1],那么a[i]=c[i]+a[i-1],由这两个式子可得a[i]=c[i]+c[i-1]+……+c[1])。

1 //https://www.luogu.org/problemnew/show/P3368 2 #include<iostream> 3 #include<cstdio> 4 using namespace std; 5 int n,m,a; 6 int c[500005]; 7 int lowbit(int x){ 8 return x&-x; 9 } 10 void add(int i,int x){ 11 while(i<=n){ 12 c[i]+=x; 13 i+=lowbit(i); 14 } 15 } 16 int query(int x){ 17 int sum=0; 18 while(x>0){ 19 sum+=c[x]; 20 x-=lowbit(x); 21 } 22 return sum; 23 } 24 int main(){ 25 scanf("%d%d",&n,&m); 26 int b=0; 27 for(int i=1;i<=n;i++){ 28 scanf("%d",&a); 29 add(i,a-b); 30 b=a; 31 } 32 print(); 33 int q,x,y,k; 34 while(m--){ 35 scanf("%d",&q); 36 if(q==1){ 37 scanf("%d%d%d",&x,&y,&k); 38 add(x,k); 39 add(y+1,-k); 40 }else{ 41 scanf("%d",&k); 42 printf("%d\n",query(k)); 43 } 44 } 45 return 0; 46 }
3:区间更新,区间查询。
我们从上面可以得到(额,求和符号写不出,看我手推的图吧)(字丑,见谅!)
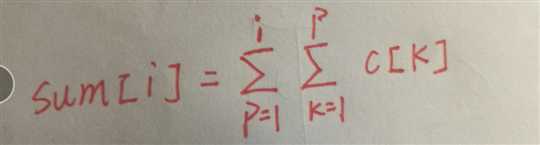
如果我们用这个式子铁定是不现实的,那我们可以再对他进行转换一下,我们可以知道c[1]加了i次,c[2]加了i-1次,……c[i]加了一次,所及就可以得出下面的化简过程:
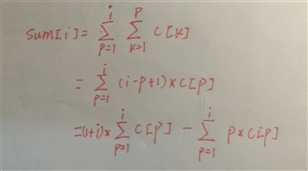
所以我们只要用两个数组数组分别维护c[p]和p*c[p]就好了,看代码吧
这里修改时c2[i]=i*(c[i]+val)=i*c[i]+i*val,所以修改偏移量是i*val.
查询就是上面推的那个式子。

1 //http://codevs.cn/problem/1082/ 2 #include<iostream> 3 #include<cstdio> 4 #define LL long long 5 using namespace std; 6 int n,m; 7 int k; 8 LL c1[200010]; 9 LL c2[200010]; 10 int lowbit(int x){ 11 return x&-x; 12 } 13 void add(LL c[200010],LL i,LL x){ 14 while(i<=n){ 15 c[i]+=x; 16 i+=lowbit(i); 17 } 18 } 19 LL getsum(LL c[200010],LL x){ 20 LL ans=0; 21 while(x>0){ 22 ans+=c[x]; 23 x-=lowbit(x); 24 } 25 return ans; 26 } 27 int main(){ 28 LL a,b=0; 29 scanf("%d",&n); 30 for(int i=1;i<=n;i++){ 31 scanf("%lld",&a); 32 add(c1,i,a-b); 33 add(c2,i,(i)*(a-b)); 34 b=a; 35 } 36 scanf("%d",&m); 37 LL x,y,v; 38 while(m--){ 39 scanf("%d",&k); 40 if(k==1){ 41 scanf("%lld%lld%lld",&x,&y,&v); 42 add(c1,x,v), add(c1,y+1,-v); 43 add(c2,x,v*x), add(c2,y+1,-(y+1)*v); 44 }else{ 45 scanf("%lld%lld",&x,&y); 46 printf("%lld\n",((y+1)*getsum(c1,y)-getsum(c2,y)) - (x*getsum(c1,x-1)-getsum(c2,x-1))); 47 } 48 } 49 return 0; 50 }
4:二维树状数组
其实二维和一维的操作是一样的,二维要用到二维前缀和sum[i][j]=sum[i-1][j]+sum[i][j-1]+sum[i-1][j-1]+a[i][j]
其它的由一维递推就好了。
(1):区间更新,单点查询
树状数组维护区间和(维护差分),(x1,y1)+val;x2+1,y2+1)+val;(x1,y2+1)-val; (x2+1,y1)-val画一个矩形框框选一下就明白了

1 //poj2155 2 #include<iostream> 3 #include<cstdio> 4 #include<queue> 5 #include<string> 6 #include<string.h> 7 #include<set> 8 #include<stack> 9 #include<vector> 10 #include<algorithm> 11 #include<cmath> 12 #include<iterator> 13 #define mem(a,b) memset(a,b,sizeof(a)) 14 #define MOD 100000007 15 #define LL long long 16 #define INF 0x3f3f3f3f 17 const double pi = acos(-1.0); 18 const int Maxn=50000; 19 using namespace std; 20 inline int scan() 21 { 22 int x=0,c=1; 23 char ch=‘ ‘; 24 while((ch>‘9‘||ch<‘0‘)&&ch!=‘-‘)ch=getchar(); 25 while(ch==‘-‘)c*=-1,ch=getchar(); 26 while(ch<=‘9‘&&ch>=‘0‘)x=x*10+ch-‘0‘,ch=getchar(); 27 return x*c; 28 } 29 30 int gcd(int a,int b){ 31 return a==0?b:gcd(b%a,a); 32 } 33 int c[1010][1010]; 34 int n,t; 35 int lowbit(int x){ 36 return x&-x; 37 } 38 void add(int x,int y){ 39 while(x<=n){ 40 int temp=y; 41 while(temp<=n){ 42 c[x][temp]++; 43 temp+=lowbit(temp); 44 } 45 x+=lowbit(x); 46 } 47 } 48 int query(int x,int y){ 49 int ans=0; 50 while(x>0){ 51 int temp=y; 52 while(temp>0){ 53 ans+=c[x][temp]; 54 temp-=lowbit(temp); 55 } 56 x-=lowbit(x); 57 } 58 return ans; 59 } 60 int main(){ 61 int x,x1,y1,x2,y2; 62 char s[2]; 63 scanf("%d",&x); 64 for(int i=1;i<=x;i++){ 65 mem(c,0); 66 scanf("%d%d",&n,&t); 67 while(t--){ 68 scanf("%s",s); 69 if(s[0]==‘C‘){ 70 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 71 add(x1,y1);///这题由于是1,0,所以一直加一输出是mod2就好了 72 add(x1,y2+1); 73 add(x2+1,y1); 74 add(x2+1,y2+1); 75 }else if(s[0]==‘Q‘){ 76 scanf("%d%d",&x1,&y1); 77 printf("%d\n",query(x1,y1)%2); 78 } 79 } 80 if(i!=x){ 81 printf("\n"); 82 } 83 } 84 return 0; 85 }
(2):区间更新,区间查询
待更新!!
标签:二叉树 下标 www. 出差 inline lowbit getch mod play
原文地址:https://www.cnblogs.com/liuzuolin/p/10827477.html