标签:nbsp ada 推导 因子 mamicode 通过 需要 height 问题
0提升的基本方法
对于分类的问题,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)要比求精确的分类的分类规则(强分类器)容易的多。提升的方法就是从弱分类器算法出发,反复学习,得到一系列弱分类器(又称为基本分类器),然后组合这些弱分类器,构成一个强分类器。大多数的提升方法都是改变训练数据集的概率分布(训练数据的权值分布),针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。
这样,对于提升方法来说,有两个问题需要回答:一是在每一轮如何改变训练数据的权值或概率分布,二是如何将弱分类器组合成一个强分类器。对于第一个问题,AdaBoost的做法是提高那些被前一轮弱分类器错误分类样本的权值,降低那些被正确分类的样本的权值。如此,那些被分类错误的样本将更加受到关注。对于第二个问题,AdaBoost采取多数表决的法法,具体的,加大分类误差率小的弱分类器的权值,使其的作用较大,减小那些分类错误率大的分类器的权值,使其在表决中起较小的作用。
1.AdaBoost算法
AdaBoost算法从训练数据中学习一系列弱分类器或者基本分类器,并将这些分类器进行线性组合。
输入:训练数据集T={(x1,y1),(x2,y2),(x3,y3)......},y的类别为{-1,1}
输出:最终的分类器G(x)
(1)初始化训练数据的权值分布
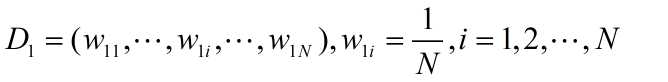
(2)对m=1,2,.....,M
(a)使用具有权值分布的Dm训练数据集进行学习,得到基本分类器
![]()
(b)计算Gm(x)在训练数据集上的分类误差率
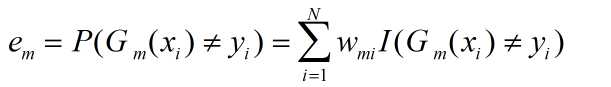
(c)计算Gm(x)的系数
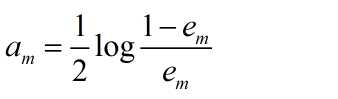
这里的对数是自然对数
(d)更新训练数据集的权值分布
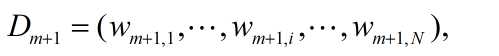
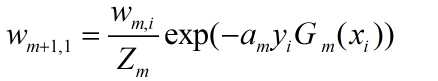
其中,Zm是归一化因子。
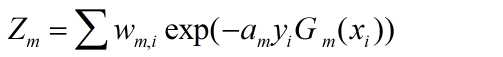
(3)构建基本的分类器的线性组合
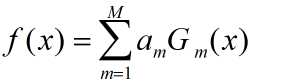
得到最终的分类器:
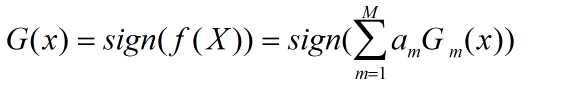
2算法详解
对于算法做如下的解释:
对于原始的数据集,假设其为均匀分布,则能够在原始数据集上面得到基本分类器。得到的权值通过改变分类误差率进而改变分类器的系数,对于基本分类器Gm(x)的系数am,am表示Gm(x)在最终分类器的重要性,当em<=0.5时,am>0,am随着em的减小而增大,所以分类误差率越小的基本分类器在最终的分类器的作用越大。
M个分类器的加权表决,系数am表示了基本分类器GM(x)的重要性,am之和并不为1,由f(x)的符号决定实例x的类,f(x)的绝对值表示分类的确信度。
标签:nbsp ada 推导 因子 mamicode 通过 需要 height 问题
原文地址:https://www.cnblogs.com/baby-lily/p/10841112.html