排序问题之冒泡排序

标签：数据   void   oid   size   bubble   name   iterator   密度   位置   

排序问题

算法问题的基础问题之一，便是排序问题：

　　输入：n个数的一个序列，<a₁, a₂,..., a_n>。

　　输出：一个排列<a_1^‘,a_2^‘, ... , a_n‘>，满足a_1^‘ ≤ a_2^‘ ≤... ≤ a_n‘ 。（输出亦可为降序，左边给出的例子为升序）

一.算法描述

      这是一个非常常见的排序算法，可能在每一个人学习排序算法的过程中，第一个接触到的就是冒泡排序。可能因为过于简单，它出现在算法导论第三版的习题2-2中。这是一种流行但低效的排序算法，在排序的过程中反复交换相邻的未按次序排列的元素，每一趟的遍历过程中将最小的元素换到序列的最前面，经过n次遍历完成排序。当然你也可以选择将最大的元素放到序列的前面去构建降序序列，或者将最大元素放到最后来构建升序序列，都不会改变算法的本质。就像啤酒中密度较小的空气泡会浮到最上方一样，冒泡排序会让最小的值排到最前面。

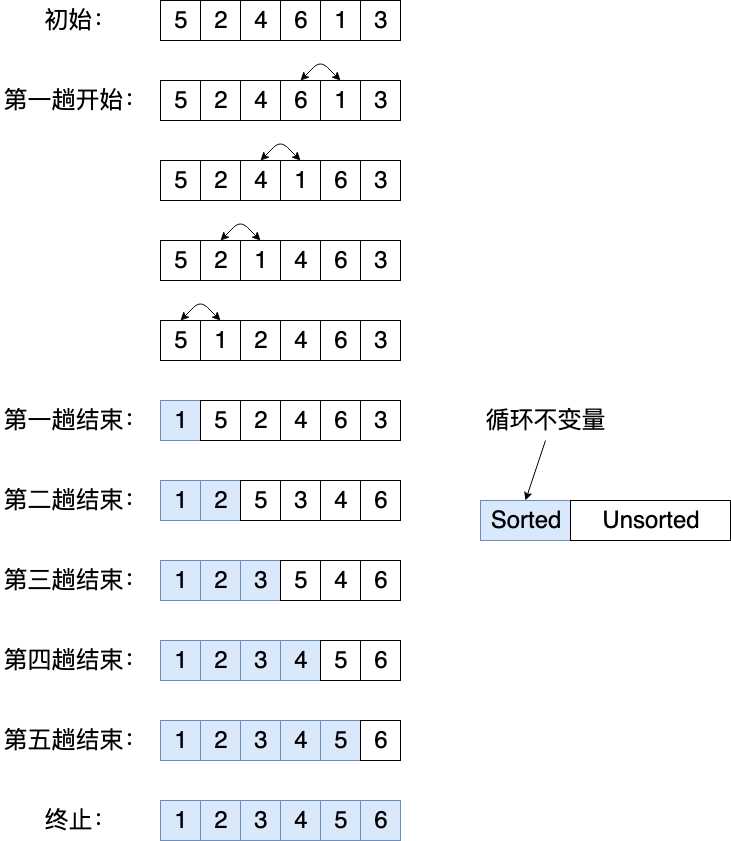
      下面我们给出一个对序列[5, 2, 4, 6, 1, 3]使用冒泡排序得到递增序列的过程，在图中蓝色的部分是排序好的序列。对于长度为n的序列，整个过程需进行n-1趟操作，每一趟将未排序的序列从右至左比较相邻两元素，如果逆序则交换位置，如图中第一趟开始到第二趟开始的过程。每进行一趟操作之后，未排序序列中的最小元素会冒泡至序列头部，sorted序列元素个数加1，unsorted序列元素个数减1，直至unsorted序列中只有一个元素时终止，这个元素为最大元素，不需进行其他操作就能得到整个序列的升序序列。

二.代码实现

      下面是冒泡排序的C++实现：

#include<iostream>
#include<vector>
using namespace std;

/**
 * @brief 对向量v进行冒泡排序
 * @param v     待排序的向量
 */
void BubbleSort(vector<int> &v)
{
    for(int i = 0; i < v.size() - 1; i++)
        for(int j = v.size() - 1; j > i; j--)
            if(v[j-1] > v[j])
                swap(v[j-1], v[j]);
}

int main()
{
    //arr为要排序的数组
    int arr[] = {5,2,4,7,10,9,8,1,6,3};

    //把数组放入向量中
    vector<int> v(arr, arr + sizeof(arr)/sizeof(int));
    
    //对向量使用插入排序
    BubbleSort(v);

    //按顺序打印排序后向量中的所有元素
    copy (v.begin(), v.end(), ostream_iterator<int> (cout, " "));
    cout << endl;
}

三.算法分析

（1）时间复杂度

　　 无论待排序的序列怎样，都要进行n-1趟遍历，共要进行n（n-1）/2次比较操作；当序列已排序时不需要进行交换操作，逆序时需要进行n（n-1）/2次交换操作。所以算法的时间复杂度为o(n²)

（2）稳定性

　　 稳定性是指对于原有序列中的等值元素，是否在排序后不改变它们的相对顺序关系。分析易知冒泡排序是稳定的。

（3）适合范围

       数据量比较小时可以使用。

（4）算法改进

排序问题之冒泡排序

标签：数据   void   oid   size   bubble   name   iterator   密度   位置   

原文地址：https://www.cnblogs.com/lovelybunny/p/10850410.html