标签:type express 不同 随机 统计 general image 基础 不清楚
Common sense reduced to computation
- Pierre-Simon, marquis de Laplace (1749–1827)
Inventor of Bayesian inference
贝叶斯方法的逻辑十分接近人脑的思维;人脑的优势不是计算,在纯数值计算方面,可以说几十年前的计算器就已经超过人脑了。
人脑的核心能力在于推理,而记忆在推理中扮演了重要的角色,我们都是基于已知的常识来做出推理。贝叶斯推断也是如此,先验就是常识,在我们有了新的观测数据后,就可以根据likelihood来更新先验,得到后验,更新常识和记忆,人类的认知进步和科学发展的逻辑也是如此。
目前,贝叶斯方法已经渗透到了生物信息和遗传统计的方方面面了,发表的文章不计其数。
学通贝叶斯方法,以后在数据分析和工具开发方面肯定就能获得一席立足之地,混口饭吃不是问题。
先学习一门课程:Module 20: Bayesian Statistics for Genetics - 超赞,值得啃完!
以下是一些笔记:
这是华盛顿大学的生物统计系的一个为期3天的培训课程,最好在三天内刷完。
搞明白几个名词之间的关系:贝叶斯方法、贝叶斯定理和贝叶斯推断。
Bayesian methods
Bayes’ Theorem (Bayes’ Rule)
Bayesian inference
想学通贝叶斯,PPT开头推荐的这几本书都得看。
贝叶斯学派和频率学派之分再次证明,看待世界的角度远不止一种,没有绝对正确之分。(相对论和量子力学)
贝叶斯公式是死的,但是看的角度是活的。the conditional probability of A given B is the conditional probability of B given A scaled by the relative probability of A compared to B.
概率论的基础框架:可重复试验、变量、概率分布。必须是可重复,不可重复事件没有概率,如果我们活在三体世界也是没有概率的,因为不可预测。
贝叶斯定理的核心,从两个对称的角度达到同一个目的:交集,但交集并不重要,我们看中的是它连接的两端。
疾病诊断的一个常识,如果疾病是小概率事件(小于0.01),那么即使诊断的特异性和敏感性都很好(大于0.9),即使你被诊断为阳性,你真为阳性的概率仍然很低。原因就是分子太小,分母得足够小才行,也就是特异性必须达到0.99才行。韦恩图真厉害,得知癌症发病率、特异性和敏感性,就可以算出venn图中每一部分的面积。
特别注意:venn图是很有效的可视化方式,假设总的面积为1,那么其中的面积就是每一部分发生的概率。事件的加、减、乘都可以同步到面积的操作上。但是到条件概率时就要小心了,条件概率改变了限定空间,也就是不能继续使用全集作为基数了。这也就是为什么:In particular, it is always true that: Pr(A|B) + Pr(非A|B) = 1. In contrast, in general: Pr(B|A) + Pr(B|非A) != 1. Pr(A|B) 和 Pr(非A|B) 改变了限定空间,在B这个space,所以的事件都可以归为两类A和非A,所以其和为1.
微积分、概率论和贝叶斯是如何联系在一起的?如果分布函数写成密度函数的形式,那么特定事件的概率就是其中的面积,积分就是求面积的专家。对于二维变量,就开始涉及到边际密度函数(就是固定其中的一个变量)。对于二维变量,特定事件的概率就是其中的体积。
对于连续型的变量的概率分布,任何一个特定值得概率都是无限接近于0,因为无理数占绝大多数。所以对于连续型变量,我们一般都是求区间内的面积。
这句话高度总结了贝叶斯定理:Bayes’ Theorem states that the conditional density is proportional to the marginal scaled by the other conditional density.
贝叶斯和频率学派是从哪个地方开始发生分歧的?非常重要!
虽然先验的形式不重要,但是贝叶斯方法必须要有先验!贝叶斯方法里必须有一个假设的模型,用于计算likelihood。
普通概率和likelihood的区别?都是一个条件概率P(data | parameter),如果固定parameter,那就是普通的条件概率;如果固定data,那就是似然函数,可以写作L(parameter | data).
假设检验就是纯频率派的方法。频率派假设噪音是普遍存在的,所以才有了小概率事件的定义。可重复试验在频率学派中至关重要。
频率学派的所有pvalue都对应了一个基本假设。
CI则是独立的,贝叶斯和频率学派都在用。
In addition to describing random variables, Bayesian statistics uses the ‘language’ of probability to describe what is known about unknown parameters.
Frequentist statistics , e.g. using p-values & confidence intervals, does not quantify what is known about parameters.
进入到贝叶斯推断,从此刻开始,我们要限定范围了,我们研究的主体明确了,那就是数据data和参数parameter。我们认为参数是服从一个概率分布的,它并没有真实值(我们不care),然后根据我们观察到的数据,可以不断更新参数的概率分布。PPT里以射箭为例。开始我们的先验的概率分布可能是非常分散的,一旦有了数据后就开始集中。
在有新数据后,贝叶斯是如何更新我们的认知的?非常重要!
Prior distribution: what you know about parameter θ, excluding the information in the data – denoted p(θ)
Likelihood: based on modeling assumptions, how (relatively) likely the data y are if the truth is θ – denoted p(y|θ)
这里对Likelihood的解释非常到位,基于模型的假设(正态分布),如果参数是真的,那么我们数据出现的概率是多少?
贝叶斯的更新过程的核心就是下面这个正比的公式:后验分布正比于先验分布乘以Likelihood。(就是先验*不同先验下数据发生的概率)

频率学派假设真的参数是存在的,利用小概率事件0.05,重复射箭很多次后,应该有95%的圈内包含了真实参数。
In almost all frequentist inference, confidence intervals take the form θˆ ± 1.96 × stderr where the standard error quantifies the ‘noise’ in some estimate θˆ of parameter θ.
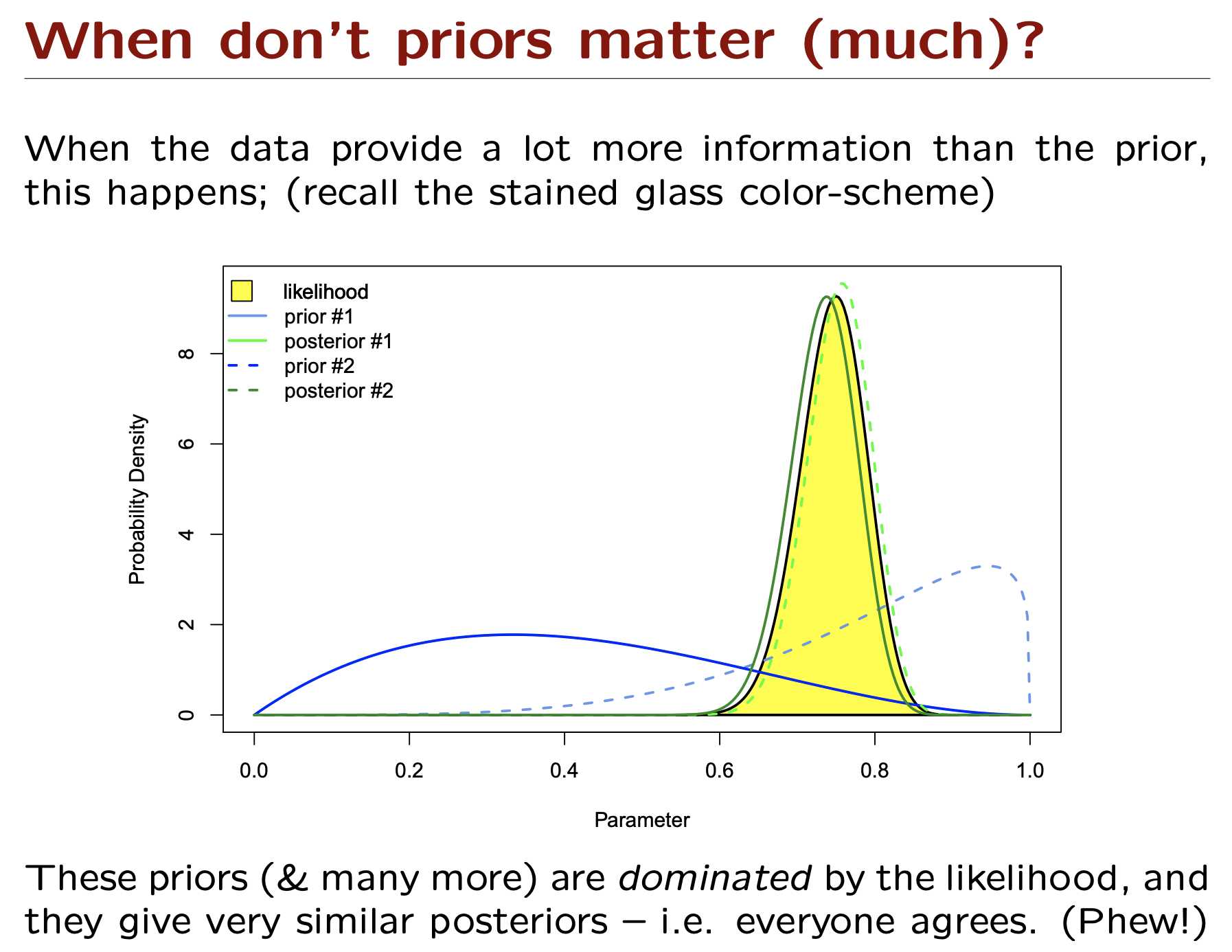
贝叶斯的更新知识的过程可以被下面这个图很好的可视化。
posterior ∝ prior × likelihood,先验、后验和似然函数都是关于参数的分布函数,所以可以统一在一幅图里可视化。
从下图中可以看到在likelihood不变的情况下,prior对posterior的影响。prior和likelihood提供的信息度很重要,当概率分布扁平的时候提供的信息就少了。
当数据量足够时,结合bayes和confidence intervals就更加顺畅了,因为贝叶斯最关心的就是参数的概率分布。
如何理解遗传过程中的概率事件?精子和卵子内携带的等位基因就是一个随机的可看做可重复的过程。减数分裂时只有一半的遗传物质能进入生殖细胞。‘Mendelian inheritance’ means that, at conception, a biological coin toss determines which parental alleles are passed on.
同一个家系中,两个后代间某个位点等位基因相同的概率也是一个概率学的问题。The probability of being ‘identical by descent’ at any locus depends on the pedigree’s genotypes, and structure.
需要先看一篇文章,PPT里使用该文章作为一个案例。
核心的问题并不难理解:本例有两个酵母菌株BY和RM,我们想知道allel对基因表达有无影响。
做了混合基因表达测序,这个问题可以看做一个二项抽样问题。
传统的非贝叶斯检验只能检验有无差异,就和差异基因一样,假设没有差异,再通过二项分布来得出结论。
缺点就是:无法得知具体的差异程度;不好设定阈值;多重检验问题;(貌似现在的DEG工具都给解决了)
下面又开始回顾贝叶斯理论了,这样其实挺好,在实例中解释所有概念会更生动一些。
贝叶斯方法的核心:how to assign prior probabilities or specify sampling models (likelihoods)
PMF和PDF的联系和区别?为什么必须要从这两个角度来衡量随机变量的概率分布?PMF的定义很直觉,就是随机变量每个值对应的各自概率。问题来了,对于连续型随机变量是画不出PMF,所以PDF就诞生了,对于连续型随机变量我们是不会在意一个点的,我们只在乎区间,PDF就是通过积分来求区间概率的。PDF是如何产生的呢?
统计分布可以看这篇文章:统计分布汇总 | 生物信息学应用 | R代码 | Univariate distribution relationships
Simply put, to carry out a Bayesian analysis one must specify a likelihood (probability distribution for the data) and a prior (beliefs about the parameters of the model).
贝叶斯方法主要应用在以下三个方面:
1. Estimation: marginal posterior distributions on parameters of interest.
2. Hypothesis Testing: Bayes factors give the evidence in the data with respect to two or more hypotheses, and provide one approach.
3. Prediction: via the predictive distribution.
怎么计算likelihood就是贝叶斯的关键了!
最大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
求最大似然函数估计值的一般步骤:
(1) 写出似然函数
(2) 对似然函数取对数,并整理
(3) 求导数
(4) 解似然方程
Bayesian Statistics for Genetics | 贝叶斯与遗传学
标签:type express 不同 随机 统计 general image 基础 不清楚
原文地址:https://www.cnblogs.com/leezx/p/10849820.html