标签:细节 元素 优化方案 部分 移动 代码实现 数据 amp 实现
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
实现说明
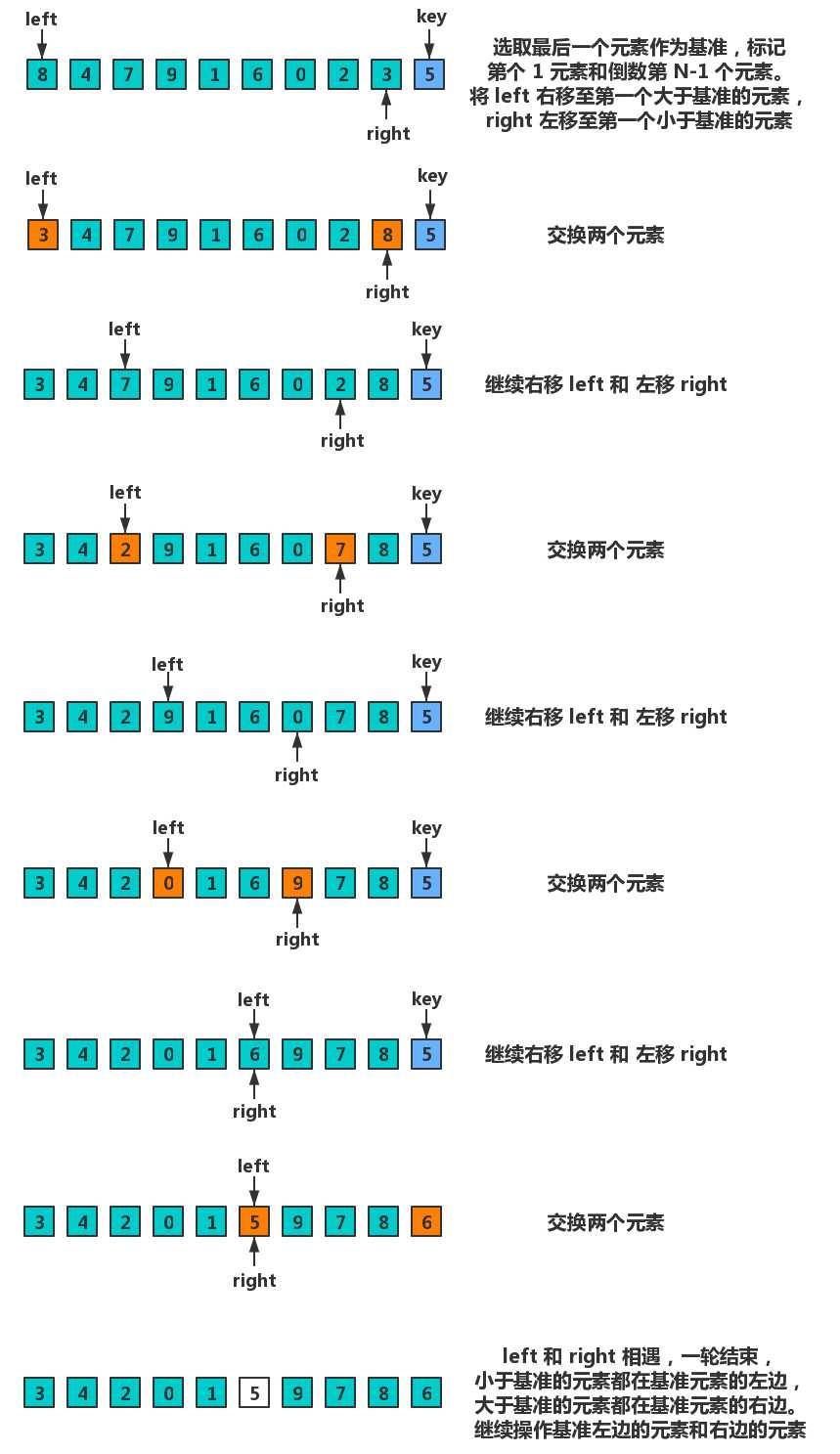
代码实现
public static void sort1(int[] arr, int start, int end) {
if (start >= end) {
return;
}
int key = end;
int left = start;
int right = end - 1;
int temp;
//当left和right相遇时结束
while (left < right) {
//移动left至第一个大于基准的元素
while (left < right && arr[left] <= arr[key]) {
left++;
}
//移动right至第一个小于基准的元素
while (left < right && arr[right] >= arr[key]) {
right--;
}
//交换left和right元素
temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
//交换相遇位置和基准
if (arr[left] > arr[key]) {
temp = arr[left];
arr[left] = arr[key];
arr[key] = temp;
}
//递归
sort1(arr, start, left - 1);
sort1(arr, right + 1, end);
}细节说明
下面的代码为什么还要判断left < right?
while (left < right && arr[left] <= arr[key]) key是序列的最后一个,right是key前一个位置,如果arr[right]=arr[key],满足arr[left]<=arr[key],然后left++,这时候left就会移动到key的位置
出了while循环并不是直接进行交换
if (arr[left] > arr[key]) {
temp = arr[left];
arr[left] = arr[key];
arr[key] = temp;
}当left和right重合时,由于不满足left<right退出while循环不会继续右移left,若此时left元素依然小于基准元素则无需进行交换。
实现说明
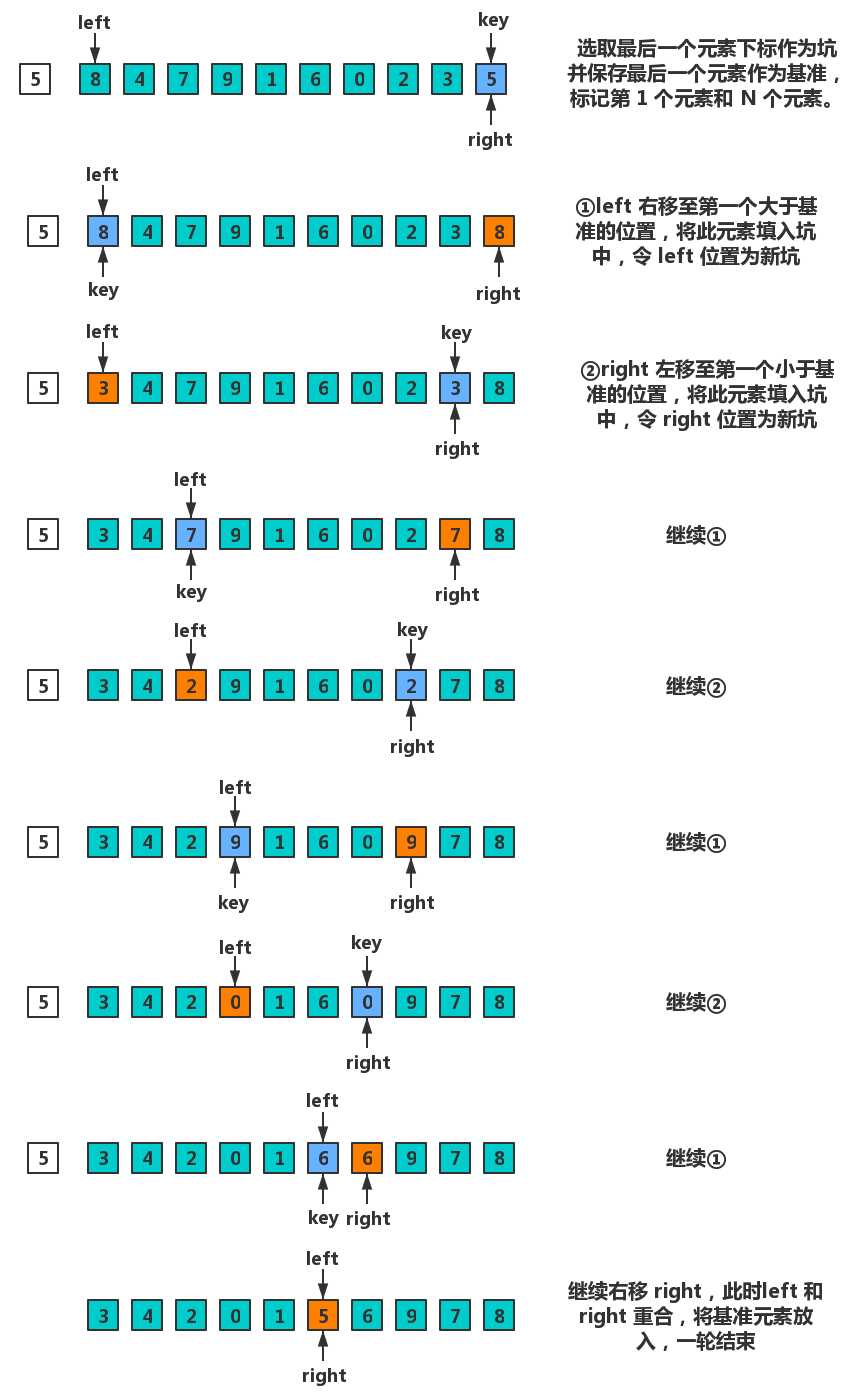
代码实现
public static void sort2(int[] arr, int start, int end) {
if (start >= end) {
return;
}
int mark = arr[end];
int left = start;
int right = end;
int key = end;
//当left和right重合时结束
while (left < right) {
//left右移至第一个大于基准的位置
while (left < right && arr[left] <= mark) {
left++;
}
//将left元素填入坑中,令left位置为新坑
arr[key] = arr[left];
key = left;
//right左移至第一个小于基准的位置
while (left < right && arr[right] >= mark) {
right--;
}
//将right元素填入坑中,令right位置为新坑
arr[key] = arr[right];
key = right;
}
//将基准元素放入重合位置
arr[left] = mark;
sort2(arr, start, left - 1);
sort2(arr, right + 1, end);
}由于坑位和right都为end,进行简化
public static void sort3(int[] arr, int start, int end) {
if (start >= end) {
return;
}
int mark = arr[end];
int left = start;
int right = end;
//当left和right重合时结束
while (left < right) {
//left右移至第一个大于基准的位置
while (left < right && arr[left] <= mark) {
left++;
}
//将left元素填入坑中,令left位置为新坑
arr[right] = arr[left];
//right左移至第一个小于基准的位置
while (left < right && arr[right] >= mark) {
right--;
}
//将right元素填入坑中,令right位置为新坑
arr[left] = arr[right];
}
//将基准元素放入重合位置
arr[left] = mark;
sort2(arr, start, left - 1);
sort2(arr, right + 1, end);
}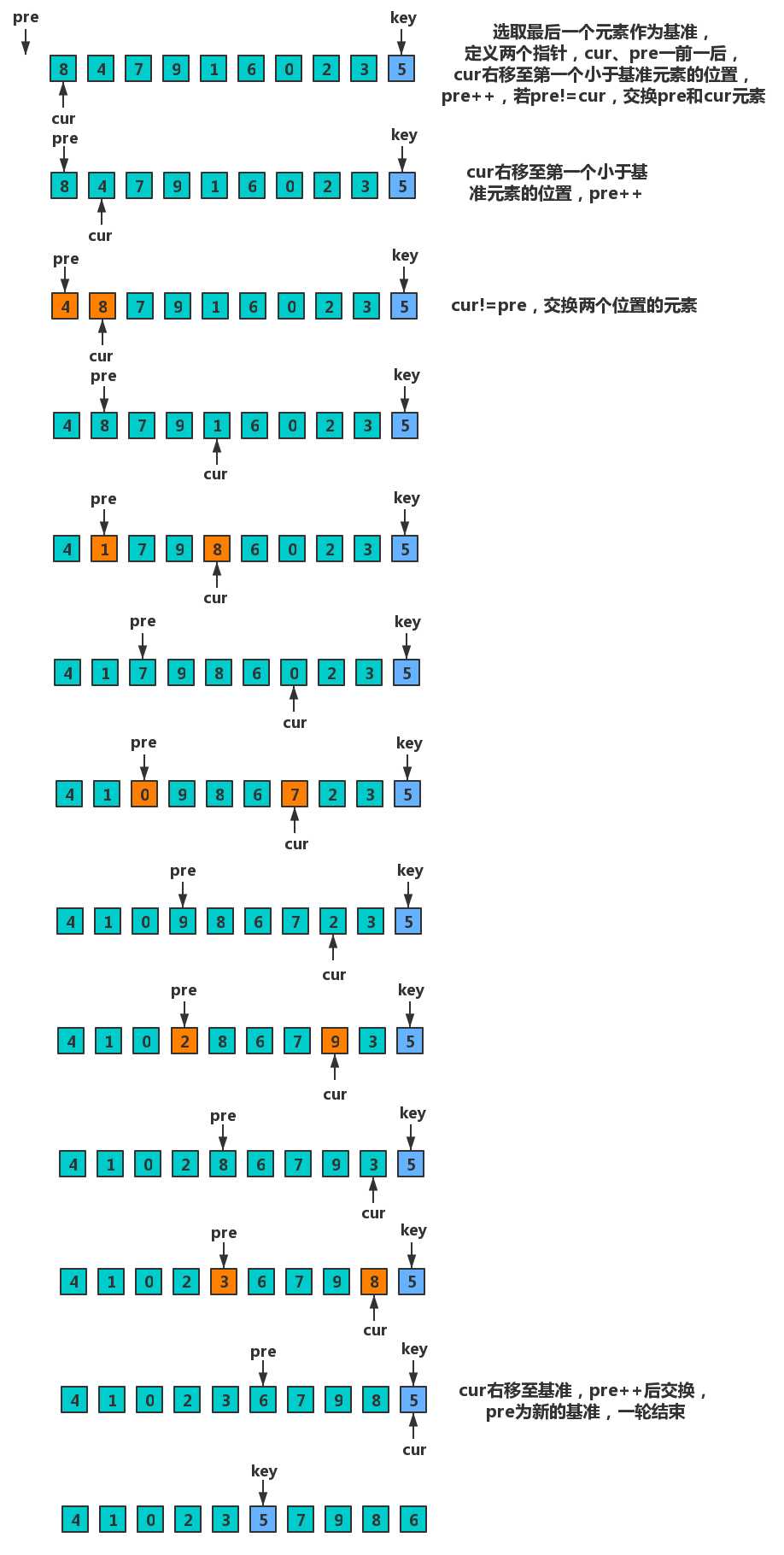
代码实现
public static void sort4(int[] arr, int start, int end){
if (start >= end) {
return;
}
int key = end;
int cur = start;
int pre = cur - 1;
int temp;
//结束循环时cur在基准处
while (cur < key) {
//当cur元素小于基准元素时才会pre++
if (arr[cur] < arr[key] && ++pre != cur) {
temp = arr[cur];
arr[cur] = arr[pre];
arr[pre] = temp;
}
cur++;
}
temp = arr[cur];
arr[cur] = arr[++pre];
arr[pre] = temp;
sort4(arr, start, pre - 1);
sort4(arr, pre + 1, end);
}选用待排数组最左边、最右边和最中间的三个元素的中间值作为基准
在待排序列是部分有序时,固定选取枢轴使快排效率底下,要缓解这种情况,就引入了随机选取枢轴
当分区的规模达到一定小时,停止快速排序算法,使用选择排序等算法
在一次分割结束后,可以把与Key相等的元素聚在一起,继续下次分割时,不用再对与key相等元素分割
在划分过程中,把与key相等元素放入数组的两端
划分结束后,把与key相等的元素移到基准周围
标签:细节 元素 优化方案 部分 移动 代码实现 数据 amp 实现
原文地址:https://www.cnblogs.com/yxmhl/p/10884280.html