标签:输入 告诉 爱情 读取文件 sys percent beautiful ade 原理
目录
不知道有没有喜欢看电影的同学,今天我们先不讲我们的 k-近邻算法,我们来讲讲电影。
可能有的同学喜欢看恐怖片,可能男生比较喜欢看爱情片,也有可能我们的女同学喜欢看动作片。那同学们你们有没有想过,我们所说的恐怖片、爱情片和动作片都是以什么来划分的呢?。。。对,有些同学已经讲到重点了,动作片中可能打斗场景较多;爱情片会存在接吻的镜头。但是,可能有些同学已经想到了。。。对,虽然动作片中会有较多的打斗场景,那么你们有没有想过某些动作片中会有接吻的镜头,爱情片也是这样。但是,有一点我们是需要清楚的,假设电影只有两个分类——动作片和爱情片二分类问题适合入门,动作片的打斗场景相对于爱情片一定是较多的,而爱情片的接吻镜头相对于动作片是较多的,确定这一点后,通过这一点我们就能判断一部电影的类型了。
k-近邻算法:测量不同特征值之间的距离方法进行分类
优点:精度高、对异常值不敏感、无数据输入假定。
缺点:计算复杂度高、空间复杂度高。
使用数据类型:数值型和标称型。
k-近邻算法(kNN)工作原理:
相信大家对 k-近邻算法有了一个大概的了解,对他需要做什么有了一定的了解,但是由于他的抽象,你们可能还是似懂非懂,这个时候我们来到我们之前所叙述的电影分类的例子中,刚刚我们得出了一个结论——动作片的打斗场景多余爱情片;爱情片的接吻场景大于动作片,那现在我们有一部没有看过的电影,我们如何确定它是爱情片还是动作片呢?当然,有的同学已经想到了。。。使用我们的 kNN 来解决这个问题。
? 图2-1 使用打斗和接吻镜头数分类
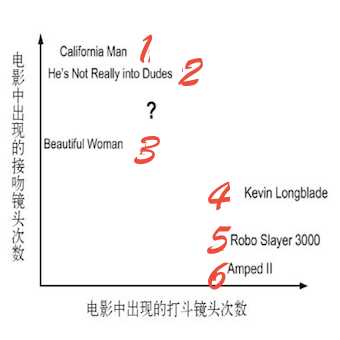
通过图2-1我们能很清晰的看到每个电影纯在多少个打斗镜头和接吻镜头。
? 表2-1 每部电影的打头镜头和接吻镜头次数和电影类型
| 序号 | 电影名称 | 打斗镜头 | 接吻镜头 | 电影类型 |
|---|---|---|---|---|
| 1 | California Man | 3 | 104 | 爱情片 |
| 2 | He’s Not Really into Dudes | 2 | 100 | 爱情片 |
| 3 | Beautiful Woman | 1 | 81 | 爱情片 |
| 4 | Kevin Longblade | 101 | 10 | 动作片 |
| 5 | Robo Slayer 3000 | 99 | 5 | 动作片 |
| 6 | Amped II | 98 | 2 | 动作片 |
| 7 | ? | 18 | 90 | 未知 |
很明显通过表2-1我们无法得知’?’是什么类型的电影。但是我们可以按照刚刚的思路计算未知电影与其他电影的距离。如表2-2所示。暂时不要关心这个数据是怎么算出来的,你目前只需要跟着我的思路走,等下一切自会揭晓。
? 表2-2 已知电影与未知电影的距离
| 序号 | 电影名称 | 与未知电影的距离 |
|---|---|---|
| 1 | California Man | 20.5 |
| 2 | He’s Not Really into Dudes | 18.7 |
| 3 | Beautiful Woman | 19.2 |
| 4 | Kevin Longblade | 115.3 |
| 5 | Robo Slayer 3000 | 117.4 |
| 6 | Amped II | 118.9 |
我们可以从表2-2中找到 k 个距离’?’最近的电影。我们假设 k=3,则这三个最靠近的电影依次是He’s Not Really into Dudes、Beautiful Woman和 California Man。通过 k-近邻算法的结论,我们发现这3部电影都是爱情片,因此我们判定未知电影是爱情片。
通过对电影类型的判断,相信同学们对 k-近邻算法有了一个初步的认识。
下面我将带大家简单的了解下 k-近邻算法的流程:
1. 收集数据:提供文本文件
2. 准备数据:对文本文件的数据做处理
3. 分析数据:检查数据确保它符合要求
4. 训练算法:此步骤不适用于 k-近邻算法
5. 测试算法:使用测试样本测试
6. 使用算法:构建一个完整的应用程序
# kNN.py
from numpy import *
import operator
def create_data_set():
"""
初始化数据,其中group 数组的函数应该和标记向量 labels 的元素数目相同。
:return: 返回训练样本集和标记向量
"""
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # 创建数据集
labels = ['A', 'A', 'B', 'B'] # 创建标记
return group, labels
由于我们大脑的限制,我们通常只能处理可视化为三维以下的事务,当然也为了以后课程的易于理解,我们对于每个数据点通常只使用两个特征。主要使用多个特征就需要经常使用线性代数的知识,只要你对一个特征、两个特征把握准确了,特征多了也不过是多加几个参数而已。
数组中的每一组数据对应一个标记,即[1.0, 1.1]对应’A’、[0, 0.1]对应’B’,当然,例子中的数值是你可以定制化设计的。我们可以通过四组数据画出他们的图像。
? 图2-2 k-近邻算法_带有四个数据点的简单例子
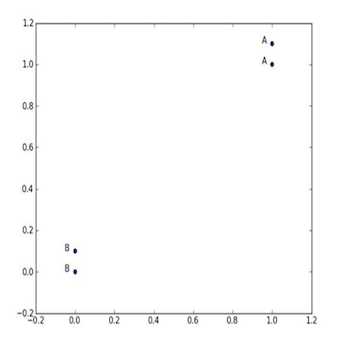
数据准备好了,下面就是我们的动手时间了。
# 伪代码
1. 计算已知类别数据集中的点与当前点之间的距离。
2. 按照距离递增次序排序。
3. 选取与当前点距离最小的 k 个点。
4. 确定前 k 个点多在类别的出现频率。
5. 返回前 k 个点出现频率最高的类别作为当前点的预测分类。
1??在kNN.py中使用欧氏距离计算两个向量\(x_A\)和\(x_B\)之间的距离:
? \[d=\sqrt{(x_{A_0}-x_{B_0})^2+(x_{A_1}-{x_{B_1}})^2}\]
例如,点\((0,0)\)与\((1,2)\)之间的距离计算为:
? \(\sqrt{(1-0)^2+(2-0)^2}\)
如果数据集存在4个特征值,则点\((1,0,0,1)\)与\((7,6,9,4)\)之间的距离计算为:
? \(\sqrt{(7-1)^2+(6-0)^2+(9-0)^2+(4-1)^2}\)
2??计算完所有点的距离后,对数据从小到大排序后确定 k 个距离最小元素所在的主要分类。输入的 k 是正整数。
3??最后将 class_count 字典分解为元祖列表,然后导入 operator.itemgetter 方法按照第二个元素的次序对元组进行从大到小的排序,之后返回发生频率最高的元素标签。
目前我们已经成功构造了一个分类器,相信在接下来的旅途中,我们构造使用分类算法将会更加容易。
# kNN.py
from numpy import *
import operator
def create_data_set():
"""
初始化数据,其中group 数组的函数应该和标记向量 labels 的元素数目相同。
:return: 返回训练样本集和标记向量
"""
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # 创建数据集
labels = ['A', 'A', 'B', 'B'] # 创建标记
return group, labels
def classify0(in_x, data_set, labels, k):
"""
对上述 create_data_set 的数据使用 k-近邻算法分类。
:param in_x: 用于分类的向量
:param data_set: 训练样本集
:param labels: 标记向量
:param k: 选择最近的数据的数目
:return:
"""
data_set_size = data_set.shape[0] # 计算训练集的大小
# 4
# 距离计算
# tile(inX, (a, b)) tile函将 inX 重复 a 行,重复 b 列
# … - data_set 每个对应的元素相减,相当于欧式距离开平房内的减法运算
diff_mat = tile(in_x, (data_set_size, 1)) - data_set
'''
[[-1. -1.1]
[-1. -1. ]
[ 0. 0. ]
[ 0. -0.1]]
'''
# 对 diff_mat 内部的每个元素平方
sq_diff_mat = diff_mat ** 2
'''
[[1. 1.21]
[1. 1. ]
[0. 0. ]
[0. 0.01]]
'''
# sum(axis=0) 每列元素相加,sum(axis=1) 每行元素相加
sq_distances = sq_diff_mat.sum(axis=1)
# [2.21 2. 0. 0.01]
# 每个元素开平方求欧氏距离
distances = sq_distances ** 0.5
# [1.48660687 1.41421356 0. 0.1 ]
# argsort函数返回的是数组值从小到大的索引值
sorted_dist_indicies = distances.argsort()
# [2 3 1 0]
# 选择距离最小的 k 个点
class_count = {} # type:dict
for i in range(k):
# 取出前 k 个对应的标签
vote_ilabel = labels[sorted_dist_indicies[i]]
# 计算每个类别的样本数
class_count[vote_ilabel] = class_count.get(vote_ilabel, 0) + 1
# operator.itemgetter(0) 按照键 key 排序,operator.itemgetter(1) 按照值 value 排序
# reverse 倒序取出频率最高的分类
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
# [('B', 2), ('A', 1)]
# 取出频率最高的分类结果
return sorted_class_count[0][0]
if __name__ == '__main__':
group, labels = create_data_set()
print(classify0([0, 0], group, labels, 3))
7上文我们已经使用 k-近邻算法构造了一个分类器分类的概念是在已有数据的基础上学会一个分类函数或构造出一个分类模型,即分类器。上一章节我已经讲到,机器学习并不是真正的预言家,k-近邻算法也是机器学习算法中的一种,因此它的答案并不总是正确的,正如上章节所讲,他会受到多种因素的影响,如训练集的个数、训练数据的特征等。上述的 k-近邻算法由于训练集的个数以及训练数据的特征远远不够的,因此他并没有太大的实际用处,下面将带大家深入 k-近邻算法。
工作一段时间后的你寂寞难耐,所以你准备去相亲网站找男/女朋友。在某个在线约会网站上,经过几个月总结,你发现你曾交往过三种类型的人:
1. 不喜欢的人
2. 魅力一般的人
3. 极具魅力的人
虽然你自己总结出了这三类人,但是约会网站无法对你接触的人通过这三种分类帮你做出确切的判断。也许你周一至周五想约会那些魅力一般的人,而周末想约会那些极具魅力的人,所以做出确切的判断很有必要。因此你收集了一些约会网站未曾记录的数据信息,想自己做个分类软件给相亲网站的产品经理,让他帮你把你的分类软件部署到他们网站上。下面就让我们来动手实现…
1. 收集数据:提供文本文件
2. 准备数据:使用 Python 解析文本文件
3. 分析数据:使用 Matplotlib 画二维散点图
4. 训练算法:此步骤不适用于 k-近邻算法
5. 测试算法:使用你提供的部分数据作为测试样本。
6. 使用算法:对心得约会对象进行预测。
测试样本:测试样本是已经完成分类的数据,既有标记,而非测试样本没有标记,因此使用你的测试算法去判断你的测试数据,如果预测类别与实际类别不同,则标记为一个错误。
其实应该叫做采集数据更专业,否则你也可以私底下称为爬虫?
你可以从我的 git 上第二章下载 datingTestSet.txt的文件,该文件每个样本数据占据一行,总共有1000行。每个样本包含三个特征:
1. 每年的飞行里程数
2. 玩视频游戏所耗时间百分比
3. 每周消费的冰淇淋公升数。
在把上述特征输入到分类器之前,我们需要新建file2matrix函数先处理输入格式问题。
# kNN.py
def file2matrix(filename):
with open(filename, 'r', encoding='utf-8') as fr:
# 获取文件的行数
array_0_lines = fr.readlines() # type:list
number_of_lines = len(array_0_lines)
# 创建以零填充的的 NumPy 矩阵,并将矩阵的另一维度设置为固定值3
return_mat = zeros((number_of_lines, 3)) # 创建一个1000行3列的0零矩阵
# 解析文件数据到列表
class_label_vector = [] # 把结果存储成列向量
index = 0
# 书本内容(错误)
# for line in fr.readlines():
# line = line.strip()
# list_from_line = line.split("\t")
# return_mat[index, :] = list_from_line[0:3]
# class_label_vector.append(int(list_from_line[-1]))
# index += 1
# 自己编写
for line in array_0_lines:
line = line.strip()
list_from_line = line.split("\t")
# return_mat 存储每一行数据的特征值
return_mat[index, :] = list_from_line[0:3]
# 通过数据的标记做分类
if list_from_line[-1] == "didntLike":
class_label_vector.append(int(1))
elif list_from_line[-1] == "smallDoses":
class_label_vector.append(int(2))
elif list_from_line[-1] == "largeDoses":
class_label_vector.append(int(3))
index += 1
return return_mat, class_label_vector话不多说,直接上代码
# kNN.py
from numpy import *
import operator
def create_data_set():
"""
初始化数据,其中group 数组的函数应该和标记向量 labels 的元素数目相同。
:return: 返回训练样本集和标记向量
"""
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # 创建数据集
labels = ['A', 'A', 'B', 'B'] # 创建标记
return group, labels
def classify0(in_x, data_set, labels, k):
"""
对上述 create_data_set 的数据使用 k-近邻算法分类。
:param in_x: 用于分类的向量
:param data_set: 训练样本集
:param labels: 标记向量
:param k: 选择最近的数据的数目
:return:
"""
data_set_size = data_set.shape[0] # 计算训练集的大小
# 4
# 距离计算
# tile(inX, (a, b)) tile函将 inX 重复 a 行,重复 b 列
# … - data_set 每个对应的元素相减,相当于欧式距离开平房内的减法运算
diff_mat = tile(in_x, (data_set_size, 1)) - data_set
'''
[[-1. -1.1]
[-1. -1. ]
[ 0. 0. ]
[ 0. -0.1]]
'''
# 对 diff_mat 内部的每个元素平方
sq_diff_mat = diff_mat ** 2
'''
[[1. 1.21]
[1. 1. ]
[0. 0. ]
[0. 0.01]]
'''
# sum(axis=0) 每列元素相加,sum(axis=1) 每行元素相加
sq_distances = sq_diff_mat.sum(axis=1)
# [2.21 2. 0. 0.01]
# 每个元素开平方求欧氏距离
distances = sq_distances ** 0.5
# [1.48660687 1.41421356 0. 0.1 ]
# argsort函数返回的是数组值从小到大的索引值
sorted_dist_indicies = distances.argsort()
# [2 3 1 0]
# 选择距离最小的 k 个点
class_count = {} # type:dict
for i in range(k):
# 取出前 k 个对应的标签
vote_i_label = labels[sorted_dist_indicies[i]]
# 计算每个类别的样本数
class_count[vote_i_label] = class_count.get(vote_i_label, 0) + 1
# operator.itemgetter(0) 按照键 key 排序,operator.itemgetter(1) 按照值 value 排序
# reverse 倒序取出频率最高的分类
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
# [('B', 2), ('A', 1)]
# 取出频率最高的分类结果
classify_result = sorted_class_count[0][0]
return classify_result
def file2matrix(filename):
with open(filename, 'r', encoding='utf-8') as fr:
# 获取文件的行数
array_0_lines = fr.readlines() # type:list
number_of_lines = len(array_0_lines)
# 创建以零填充的的 NumPy 矩阵,并将矩阵的另一维度设置为固定值3
return_mat = zeros((number_of_lines, 3)) # 创建一个1000行3列的0零矩阵
# 解析文件数据到列表
class_label_vector = [] # 把结果存储成列向量
index = 0
# 书本内容(报错)
# for line in fr.readlines():
# line = line.strip()
# list_from_line = line.split("\t")
# return_mat[index, :] = list_from_line[0:3]
# class_label_vector.append(int(list_from_line[-1]))
# index += 1
# 自己编写
for line in array_0_lines:
line = line.strip()
list_from_line = line.split("\t")
# return_mat 存储每一行数据的特征值
return_mat[index, :] = list_from_line[0:3]
# 通过数据的标记做分类
if list_from_line[-1] == "didntLike":
class_label_vector.append(int(1))
elif list_from_line[-1] == "smallDoses":
class_label_vector.append(int(2))
elif list_from_line[-1] == "largeDoses":
class_label_vector.append(int(3))
index += 1
return return_mat, class_label_vector
def scatter_diagram(dating_data_mat, dating_labels, diagram_type=1):
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# windows下配置 font 为中文字体
# font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
# mac下配置 font 为中文字体
font = FontProperties(fname='/System/Library/Fonts/STHeiti Medium.ttc')
# 通过 dating_labels 的索引获取不同分类在矩阵内的行数
index = 0
index_1 = []
index_2 = []
index_3 = []
for i in dating_labels:
if i == 1:
index_1.append(index)
elif i == 2:
index_2.append(index)
elif i == 3:
index_3.append(index)
index += 1
# 对不同分类在矩阵内不同的行数构造每个分类的矩阵
type_1 = dating_data_mat[index_1, :]
type_2 = dating_data_mat[index_2, :]
type_3 = dating_data_mat[index_3, :]
fig = plt.figure()
ax = fig.add_subplot(111) # 就是1行一列一张画布一张图,
if diagram_type == 1:
# 通过对特征0、1比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 1], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 1], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 1], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('玩视频游戏所耗时间百分比', fontproperties=font)
elif diagram_type == 2:
# 通过对特征1、2比较的散点图
type_1 = ax.scatter(type_1[:, 1], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 1], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 1], type_3[:, 2], c='green')
plt.xlabel('玩视频游戏所耗时间百分比', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
elif diagram_type == 3:
# 通过对特征0、2比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 2], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
plt.legend((type_1, type_2, type_3), ('不喜欢的人', '魅力一般的人', '极具魅力的人'), loc=4, prop=font)
plt.show()
if __name__ == '__main__':
group, labels = create_data_set()
classify0([0, 0], group, labels, 3)
import os
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
# 需要画图演示开启
'''
diagram_type = 1, 比较特征(0, 1);
diagram_type = 2, 比较特征(1, 2);
diagram_type = 3, 比较特征(0, 2)
'''
# scatter_diagram(dating_data_mat, dating_labels, diagram_type=1)
norm_mat, ranges, min_vals = auto_norm(dating_data_mat)
? 图2-3 玩视频游戏和每年飞行里程数特征比较
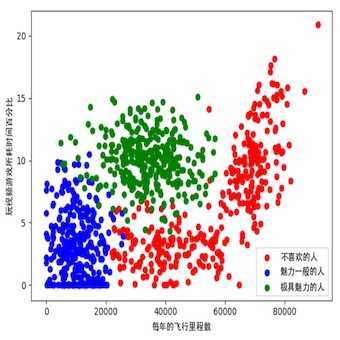
? 表2-3 四条约会网站原始数据
| 玩视频游戏所耗时间百分比 | 每年飞行里程数 | 每周消费的冰淇淋公升数 | 样本分类 | |
|---|---|---|---|---|
| 1 | 0.8 | 400 | 0.5 | 1 |
| 2 | 12 | 134000 | 0.9 | 3 |
| 3 | 0 | 20000 | 1.1 | 2 |
| 4 | 67 | 32000 | 0.1 | 2 |
如果我们要计算表2-3中样本三和样本4的距离,可以使用下面的方法:
? \(\sqrt{(0-67)^2+(20000-32000)^2+(1.1-0.1)^2}\)
但是上面方程汇总差值最大的属性对计算结果的影响很大,并且是远远大于其他两个特征的差值。但是你可能会认为以上三种特征是同等重要的,因此作为三个等权重的特征之一,第二个特征不应该严重地影响到计算结果。
为了处理这种不同取值范围的特征值时,我们通常采用归一化数值法,将特征值的取值范围处理为\(0\)到\(1\)或者\(-1\)到\(1\)之间。我们可以使用下面的公式把特征值的取值范围转化为\(0\)到\(1\)区间内的值:
? \(new_value=(old_value-min)/(max-min)\)其中\(min\) 和 \({max}\) 分别是数据集汇总的最小特征值和最大特征值。
因此我们需要在 kNN.py 文件中增加一个新函数auto_norm(),该函数可以自动将数字特征值转化为\(0\)到\(1\)的区间。
# kNN.py
def auto_norm(data_set):
# min(0)使得函数从列中选取最小值,min(1)使得函数从行中选取最小值
min_vals = data_set.min(0)
max_vals = data_set.max(0)
ranges = max_vals - min_vals
# 获取 data_set 的总行数
m = data_set.shape[0]
# 特征值相除
# 相当于公式里的old_value-min
# tile函数相当于将 min_vals 重复 m 行,重复1列
norm_data_set = data_set - tile(min_vals, (m, 1))
# 相当于公式里的(old_value-min)/(max-min)
norm_data_set = norm_data_set / tile(ranges, (m, 1))
return norm_data_set, ranges, min_vals上节我们已经将数据按照需求做了归一化数值处理,本节我们将测试分类器的效果。之前讲到过机器学习算法通常将已有数据的\(80\%\)作为训练样本,其余的\(20\%\)作为测试数据去测试分类测试数据应该是随机选择的,检测分类器的正确率。
因此我们需要在 kNN.py 文件中创建函数dating_class_test()
# kNN.py
from numpy import *
import operator
def create_data_set():
"""
初始化数据,其中group 数组的函数应该和标记向量 labels 的元素数目相同。
:return: 返回训练样本集和标记向量
"""
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # 创建数据集
labels = ['A', 'A', 'B', 'B'] # 创建标记
return group, labels
def classify0(in_x, data_set, labels, k):
"""
对上述 create_data_set 的数据使用 k-近邻算法分类。
:param in_x: 用于分类的向量
:param data_set: 训练样本集
:param labels: 标记向量
:param k: 选择最近的数据的数目
:return:
"""
data_set_size = data_set.shape[0] # 计算训练集的大小
# 4
# 距离计算
# tile(inX, (a, b)) tile函将 inX 重复 a 行,重复 b 列
# … - data_set 每个对应的元素相减,相当于欧式距离开平房内的减法运算
diff_mat = tile(in_x, (data_set_size, 1)) - data_set
'''
[[-1. -1.1]
[-1. -1. ]
[ 0. 0. ]
[ 0. -0.1]]
'''
# 对 diff_mat 内部的每个元素平方
sq_diff_mat = diff_mat ** 2
'''
[[1. 1.21]
[1. 1. ]
[0. 0. ]
[0. 0.01]]
'''
# sum(axis=0) 每列元素相加,sum(axis=1) 每行元素相加
sq_distances = sq_diff_mat.sum(axis=1)
# [2.21 2. 0. 0.01]
# 每个元素开平方求欧氏距离
distances = sq_distances ** 0.5
# [1.48660687 1.41421356 0. 0.1 ]
# argsort函数返回的是数组值从小到大的索引值
sorted_dist_indicies = distances.argsort()
# [2 3 1 0]
# 选择距离最小的 k 个点
class_count = {} # type:dict
for i in range(k):
# 取出前 k 个对应的标签
vote_i_label = labels[sorted_dist_indicies[i]]
# 计算每个类别的样本数
class_count[vote_i_label] = class_count.get(vote_i_label, 0) + 1
# operator.itemgetter(0) 按照键 key 排序,operator.itemgetter(1) 按照值 value 排序
# reverse 倒序取出频率最高的分类
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
# [('B', 2), ('A', 1)]
# 取出频率最高的分类结果
classify_result = sorted_class_count[0][0]
return classify_result
def file2matrix(filename):
with open(filename, 'r', encoding='utf-8') as fr:
# 获取文件的行数
array_0_lines = fr.readlines() # type:list
number_of_lines = len(array_0_lines)
# 创建以零填充的的 NumPy 矩阵,并将矩阵的另一维度设置为固定值3
return_mat = zeros((number_of_lines, 3)) # 创建一个1000行3列的0零矩阵
# 解析文件数据到列表
class_label_vector = [] # 把结果存储成列向量
index = 0
# 书本内容(报错)
# for line in fr.readlines():
# line = line.strip()
# list_from_line = line.split("\t")
# return_mat[index, :] = list_from_line[0:3]
# class_label_vector.append(int(list_from_line[-1]))
# index += 1
# 自己编写
for line in array_0_lines:
line = line.strip()
list_from_line = line.split("\t")
# return_mat 存储每一行数据的特征值
return_mat[index, :] = list_from_line[0:3]
# 通过数据的标记做分类
if list_from_line[-1] == "didntLike":
class_label_vector.append(int(1))
elif list_from_line[-1] == "smallDoses":
class_label_vector.append(int(2))
elif list_from_line[-1] == "largeDoses":
class_label_vector.append(int(3))
index += 1
return return_mat, class_label_vector
def scatter_diagram(dating_data_mat, dating_labels, diagram_type=1):
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# windows下配置 font 为中文字体
# font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
# mac下配置 font 为中文字体
font = FontProperties(fname='/System/Library/Fonts/STHeiti Medium.ttc')
# 通过 dating_labels 的索引获取不同分类在矩阵内的行数
index = 0
index_1 = []
index_2 = []
index_3 = []
for i in dating_labels:
if i == 1:
index_1.append(index)
elif i == 2:
index_2.append(index)
elif i == 3:
index_3.append(index)
index += 1
# 对不同分类在矩阵内不同的行数构造每个分类的矩阵
type_1 = dating_data_mat[index_1, :]
type_2 = dating_data_mat[index_2, :]
type_3 = dating_data_mat[index_3, :]
fig = plt.figure()
ax = fig.add_subplot(111) # 就是1行一列一张画布一张图,
if diagram_type == 1:
# 通过对特征0、1比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 1], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 1], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 1], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('玩视频游戏所耗时间百分比', fontproperties=font)
elif diagram_type == 2:
# 通过对特征1、2比较的散点图
type_1 = ax.scatter(type_1[:, 1], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 1], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 1], type_3[:, 2], c='green')
plt.xlabel('玩视频游戏所耗时间百分比', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
elif diagram_type == 3:
# 通过对特征0、2比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 2], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
plt.legend((type_1, type_2, type_3), ('不喜欢的人', '魅力一般的人', '极具魅力的人'), loc=4, prop=font)
plt.show()
def auto_norm(data_set):
# min(0)使得函数从列中选取最小值,min(1)使得函数从行中选取最小值
min_vals = data_set.min(0)
max_vals = data_set.max(0)
ranges = max_vals - min_vals
# 获取 data_set 的总行数
m = data_set.shape[0]
# 特征值相除
# 相当于公式里的old_value-min
# tile函数相当于将 min_vals 重复 m 行,重复1列
norm_data_set = data_set - tile(min_vals, (m, 1))
# 相当于公式里的(old_value-min)/(max-min)
norm_data_set = norm_data_set / tile(ranges, (m, 1))
return norm_data_set, ranges, min_vals
def dating_class_test():
import os
# 测试样本比率
ho_ratio = 0.20
# 读取文本数据
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
# 对数据归一化特征值处理
norm_mat, ranges, min_vals = auto_norm(dating_data_mat)
m = norm_mat.shape[0]
num_test_vecs = int(m * ho_ratio)
error_count = 0
for i in range(num_test_vecs):
# 因为你的数据本来就是随机的,所以直接选择前20%的数据作为测试数据
classifier_result = classify0(norm_mat[i, :], norm_mat[num_test_vecs:m, :], dating_labels[num_test_vecs:m], 3)
if classifier_result != dating_labels[i]: error_count += 1
print("the total error rate is: {}".format(error_count / float(num_test_vecs)))
# the total error rate is: 0.08
def main():
import os
group, labels = create_data_set()
classify0([0, 0], group, labels, 3)
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
# 需要画图演示开启
'''
diagram_type = 1, 比较特征(0, 1);
diagram_type = 2, 比较特征(1, 2);
diagram_type = 3, 比较特征(0, 2)
'''
# scatter_diagram(dating_data_mat, dating_labels, diagram_type=1)
auto_norm(dating_data_mat)
if __name__ == '__main__':
main()
dating_class_test()
运行整个算法,最后得出分类器处理约会数据集的错误率是\(8\%\),这是一个相当不错的结果。我们也可以改变测试集的比率即 ho_ratio 的值来检测错误率的变化。
刚刚已经讲到我们的算法错误率只有\(8\%\),这是一个很不错的算法了。现在我们手动实现一个小程序让我们找到某个人并输入他/她的信息,让小程序给出我们对对方喜欢程度的预测值。
# kNN.py
from numpy import *
import operator
def create_data_set():
"""
初始化数据,其中group 数组的函数应该和标记向量 labels 的元素数目相同。
:return: 返回训练样本集和标记向量
"""
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # 创建数据集
labels = ['A', 'A', 'B', 'B'] # 创建标记
return group, labels
def classify0(in_x, data_set, labels, k):
"""
对上述 create_data_set 的数据使用 k-近邻算法分类。
:param in_x: 用于分类的向量
:param data_set: 训练样本集
:param labels: 标记向量
:param k: 选择最近的数据的数目
:return:
"""
data_set_size = data_set.shape[0] # 计算训练集的大小
# 4
# 距离计算
# tile(inX, (a, b)) tile函将 inX 重复 a 行,重复 b 列
# … - data_set 每个对应的元素相减,相当于欧式距离开平房内的减法运算
diff_mat = tile(in_x, (data_set_size, 1)) - data_set
'''
[[-1. -1.1]
[-1. -1. ]
[ 0. 0. ]
[ 0. -0.1]]
'''
# 对 diff_mat 内部的每个元素平方
sq_diff_mat = diff_mat ** 2
'''
[[1. 1.21]
[1. 1. ]
[0. 0. ]
[0. 0.01]]
'''
# sum(axis=0) 每列元素相加,sum(axis=1) 每行元素相加
sq_distances = sq_diff_mat.sum(axis=1)
# [2.21 2. 0. 0.01]
# 每个元素开平方求欧氏距离
distances = sq_distances ** 0.5
# [1.48660687 1.41421356 0. 0.1 ]
# argsort函数返回的是数组值从小到大的索引值
sorted_dist_indicies = distances.argsort()
# [2 3 1 0]
# 选择距离最小的 k 个点
class_count = {} # type:dict
for i in range(k):
# 取出前 k 个对应的标签
vote_i_label = labels[sorted_dist_indicies[i]]
# 计算每个类别的样本数
class_count[vote_i_label] = class_count.get(vote_i_label, 0) + 1
# operator.itemgetter(0) 按照键 key 排序,operator.itemgetter(1) 按照值 value 排序
# reverse 倒序取出频率最高的分类
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
# [('B', 2), ('A', 1)]
# 取出频率最高的分类结果
classify_result = sorted_class_count[0][0]
return classify_result
def file2matrix(filename):
with open(filename, 'r', encoding='utf-8') as fr:
# 获取文件的行数
array_0_lines = fr.readlines() # type:list
number_of_lines = len(array_0_lines)
# 创建以零填充的的 NumPy 矩阵,并将矩阵的另一维度设置为固定值3
return_mat = zeros((number_of_lines, 3)) # 创建一个1000行3列的0零矩阵
# 解析文件数据到列表
class_label_vector = [] # 把结果存储成列向量
index = 0
# 书本内容(报错)
# for line in fr.readlines():
# line = line.strip()
# list_from_line = line.split("\t")
# return_mat[index, :] = list_from_line[0:3]
# class_label_vector.append(int(list_from_line[-1]))
# index += 1
# 自己编写
for line in array_0_lines:
line = line.strip()
list_from_line = line.split("\t")
# return_mat 存储每一行数据的特征值
return_mat[index, :] = list_from_line[0:3]
# 通过数据的标记做分类
if list_from_line[-1] == "didntLike":
class_label_vector.append(int(1))
elif list_from_line[-1] == "smallDoses":
class_label_vector.append(int(2))
elif list_from_line[-1] == "largeDoses":
class_label_vector.append(int(3))
index += 1
return return_mat, class_label_vector
def scatter_diagram(dating_data_mat, dating_labels, diagram_type=1):
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# windows下配置 font 为中文字体
# font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
# mac下配置 font 为中文字体
font = FontProperties(fname='/System/Library/Fonts/STHeiti Medium.ttc')
# 通过 dating_labels 的索引获取不同分类在矩阵内的行数
index = 0
index_1 = []
index_2 = []
index_3 = []
for i in dating_labels:
if i == 1:
index_1.append(index)
elif i == 2:
index_2.append(index)
elif i == 3:
index_3.append(index)
index += 1
# 对不同分类在矩阵内不同的行数构造每个分类的矩阵
type_1 = dating_data_mat[index_1, :]
type_2 = dating_data_mat[index_2, :]
type_3 = dating_data_mat[index_3, :]
fig = plt.figure()
ax = fig.add_subplot(111) # 就是1行一列一张画布一张图,
if diagram_type == 1:
# 通过对特征0、1比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 1], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 1], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 1], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('玩视频游戏所耗时间百分比', fontproperties=font)
elif diagram_type == 2:
# 通过对特征1、2比较的散点图
type_1 = ax.scatter(type_1[:, 1], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 1], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 1], type_3[:, 2], c='green')
plt.xlabel('玩视频游戏所耗时间百分比', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
elif diagram_type == 3:
# 通过对特征0、2比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 2], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
plt.legend((type_1, type_2, type_3), ('不喜欢的人', '魅力一般的人', '极具魅力的人'), loc=4, prop=font)
plt.show()
def auto_norm(data_set):
# min(0)使得函数从列中选取最小值,min(1)使得函数从行中选取最小值
min_vals = data_set.min(0)
max_vals = data_set.max(0)
ranges = max_vals - min_vals
# 获取 data_set 的总行数
m = data_set.shape[0]
# 特征值相除
# 相当于公式里的old_value-min
# tile函数相当于将 min_vals 重复 m 行,重复1列
norm_data_set = data_set - tile(min_vals, (m, 1))
# 相当于公式里的(old_value-min)/(max-min)
norm_data_set = norm_data_set / tile(ranges, (m, 1))
return norm_data_set, ranges, min_vals
def dating_class_test():
import os
# 测试样本比率
ho_ratio = 0.20
# 读取文本数据
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
# 对数据归一化特征值处理
norm_mat, ranges, min_vals = auto_norm(dating_data_mat)
m = norm_mat.shape[0]
num_test_vecs = int(m * ho_ratio)
error_count = 0
for i in range(num_test_vecs):
# 因为你的数据本来就是随机的,所以直接选择前20%的数据作为测试数据
classifier_result = classify0(norm_mat[i, :], norm_mat[num_test_vecs:m, :], dating_labels[num_test_vecs:m], 3)
if classifier_result != dating_labels[i]: error_count += 1
# print("the total error rate is: {}".format(error_count / float(num_test_vecs)))
# the total error rate is: 0.08
def main():
import os
group, labels = create_data_set()
classify0([0, 0], group, labels, 3)
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
# 需要画图演示开启
'''
diagram_type = 1, 比较特征(0, 1);
diagram_type = 2, 比较特征(1, 2);
diagram_type = 3, 比较特征(0, 2)
'''
# scatter_diagram(dating_data_mat, dating_labels, diagram_type=1)
auto_norm(dating_data_mat)
def classify_person():
import os
result_list = ['讨厌', '有点喜欢', '非常喜欢']
ff_miles = float(input("每年的出行公里数(km)?例如:1000\n"))
percent_tats = float(input("每年玩游戏的时间占比(.%)?例如:10\n"))
ice_cream = float(input("每年消费多少零食(kg)?例如:1\n"))
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
norm_mat, ranges, min_vals = auto_norm(dating_data_mat)
in_arr = array([ff_miles, percent_tats, ice_cream])
classifier_result = classify0((in_arr - min_vals) / ranges, norm_mat, dating_labels, 3)
print("你可能对他/她的印象:\n{}".format(result_list[classifier_result - 1]))
if __name__ == '__main__':
main()
dating_class_test()
classify_person()
? 图2-4 约会-终
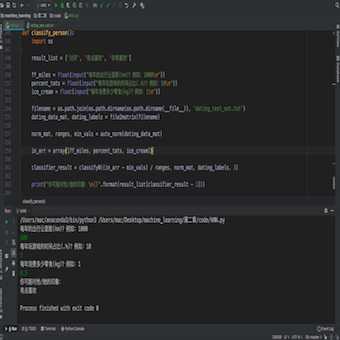
从图2-4中可以看出我们通过输入特征值得到了小程序给我们预测的结果,算是一个小小的结束。我们也实现了我们的第一个算法,我可以很自信的告诉你,你可以把这个小程序让约会网站的产品经理部署了。
聪明的同学已经发现我们这个约会小程序处理的数据都是较为容易让人理解的数据,那我们如何对不容易让人理解的数据构造一个分类器呢?接下来我们就要实现我们的第二个算法——手写识别系统。
现在让我们手动构造一个简单的手写识别系统,该系统只能识别数字\(0-9\)。
以下是我们使用 k-近邻算法实现手写识别系统需要的步骤:
1. 收集数据:提供文本文件
2. 准备数据:编写函数 calssify(),将图像格式转换为分类器使用的 list 格式
3. 分析数据:检查数据确保它符合要求
4. 训练算法:此步骤不适用于 k-近邻算法
5. 测试算法:使用测试样本测试
6. 使用算法:构建一个完整的应用程序
在 digits 文件夹内有两个子目录:目录 traininigDigits 中大约有2000个例子,每个例子的内容如图2-5所示,么个数字大约有200个样本;目录 testDigits 中包含了了大约900个测试数据,并且两组数据没有重叠。
? 图2-5 数字0的文本图

为了使用前面约会例子的分类器,我们把图像格式处理为一个向量。图像在计算机上是由一个一个像素点组成的。我们可以把本例中32*32的二进制图像矩阵转换为1*1024的向量。
下面我就来实现一个 img2vector 函数,将图像转换为向量。
# kNN.py
def img2vector(filename):
# 构造一个一行有1024个元素的矩阵
return_vect = zeros((1, 1024))
with open(filename, 'r', encoding='utf-8') as fr:
# 读取文件的每一行的所有元素
for i in range(32):
line_str = fr.readline()
# 把文件每一行的所有元素按照顺序写入构造的1*1024的零矩阵
for j in range(32):
return_vect[0, 32 * i + j] = int(line_str[j])
return return_vect
我们已经可以把单个图像的文本文件格式转化为分类器可以识别的格式了,我们接下来的工作就是要把我们现有的数据输入到分类器,检查分类器的执行效果了。因此我们来构造一个 hand_writing_class_test 方法来实现该功能。
# kNN.py
def hand_writing_class_test():
import os
# 获取训练集和测试集数据的根路径
training_digits_path = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'digits/trainingDigits')
test_digits_path = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'digits/testDigits')
# 对训练集数据做处理,构造一个 m*1024 的矩阵,m 是训练集数据的个数
hw_labels = []
training_file_list = os.listdir(training_digits_path) # type:list
m = training_file_list.__len__()
training_mat = zeros((m, 1024))
# 对训练集中的单个数据做处理
for i in range(m):
# 取出文件中包含的数字
file_name_str = training_file_list[i] # type:str
file_str = file_name_str.split('.')[0]
class_num_str = int(file_str.split('_')[0])
# 添加标记
hw_labels.append(class_num_str)
# 把该文件中的所有元素构造成 1*1024 的矩阵后存入之前构造的 m*1024 的矩阵中对应的行
training_mat[i, :] = img2vector(os.path.join(training_digits_path, file_name_str))
# 对测试集数据做处理,构造一个 m*1024 的矩阵,m 是测试集数据的个数
test_file_list = os.listdir(test_digits_path)
error_count = 0
m_test = test_file_list.__len__()
# 对测试集中的单个数据做处理
for i in range(m_test):
# 取出文件中包含的数字
file_name_str = test_file_list[i]
file_str = file_name_str.split('.')[0]
class_num_str = int(file_str.split('_')[0])
# 把该文件中的所有元素构造成一个 1*1024 的矩阵
vector_under_test = img2vector(os.path.join(test_digits_path, file_name_str))
# 对刚刚构造的 1*1024 的矩阵进行分类处理判断结果
classifier_result = classify0(vector_under_test, training_mat, hw_labels, 3)
# 对判断错误的计数加 1
if classifier_result != class_num_str: error_count += 1
print("错误率: {}".format(error_count / float(m_test)))
# 错误率: 0.010570824524312896
k-近邻算法识别手写数字数据集,错误率为1%。如约会的例子,如果我们改变 k 的值,修改训练样本或者测试样本的数据,都会对 k-近邻算法的准确率产生一定的影响,感兴趣的可以自己测试。
既然我们刚刚实现的算法错误率仅有1%。那为什么我们不手动实现一个系统通过输入图片然后识别图片上的数字呢?那就让我们开动吧!仅做参考,涉及知识点过多,不感兴趣的同学可以跳过。为了实现该系统,首先我们要手写一个img_binaryzation 方法对图片的大小修改成我们需要的 32*32px,然后对图片进行二值化处理生成一个.txt文件,之后我们把该 .txt文件传入我们的 hand_writing_test 方法中得到结果。
# kNN.py
from numpy import *
import operator
def create_data_set():
"""
初始化数据,其中group 数组的函数应该和标记向量 labels 的元素数目相同。
:return: 返回训练样本集和标记向量
"""
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # 创建数据集
labels = ['A', 'A', 'B', 'B'] # 创建标记
return group, labels
def classify0(in_x, data_set, labels, k):
"""
对上述 create_data_set 的数据使用 k-近邻算法分类。
:param in_x: 用于分类的向量
:param data_set: 训练样本集
:param labels: 标记向量
:param k: 选择最近的数据的数目
:return:
"""
data_set_size = data_set.shape[0] # 计算训练集的大小
# 4
# 距离计算
# tile(inX, (a, b)) tile函将 inX 重复 a 行,重复 b 列
# … - data_set 每个对应的元素相减,相当于欧式距离开平房内的减法运算
diff_mat = tile(in_x, (data_set_size, 1)) - data_set
'''
[[-1. -1.1]
[-1. -1. ]
[ 0. 0. ]
[ 0. -0.1]]
'''
# 对 diff_mat 内部的每个元素平方
sq_diff_mat = diff_mat ** 2
'''
[[1. 1.21]
[1. 1. ]
[0. 0. ]
[0. 0.01]]
'''
# sum(axis=0) 每列元素相加,sum(axis=1) 每行元素相加
sq_distances = sq_diff_mat.sum(axis=1)
# [2.21 2. 0. 0.01]
# 每个元素开平方求欧氏距离
distances = sq_distances ** 0.5
# [1.48660687 1.41421356 0. 0.1 ]
# argsort函数返回的是数组值从小到大的索引值
sorted_dist_indicies = distances.argsort()
# [2 3 1 0]
# 选择距离最小的 k 个点
class_count = {} # type:dict
for i in range(k):
# 取出前 k 个对应的标签
vote_i_label = labels[sorted_dist_indicies[i]]
# 计算每个类别的样本数
class_count[vote_i_label] = class_count.get(vote_i_label, 0) + 1
# operator.itemgetter(0) 按照键 key 排序,operator.itemgetter(1) 按照值 value 排序
# reverse 倒序取出频率最高的分类
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
# [('B', 2), ('A', 1)]
# 取出频率最高的分类结果
classify_result = sorted_class_count[0][0]
return classify_result
def file2matrix(filename):
with open(filename, 'r', encoding='utf-8') as fr:
# 获取文件的行数
array_0_lines = fr.readlines() # type:list
number_of_lines = array_0_lines.__len__()
# 创建以零填充的的 NumPy 矩阵,并将矩阵的另一维度设置为固定值3
return_mat = zeros((number_of_lines, 3)) # 创建一个1000行3列的0零矩阵
# 解析文件数据到列表
class_label_vector = [] # 把结果存储成列向量
index = 0
# 书本内容(报错)
# for line in fr.readlines():
# line = line.strip()
# list_from_line = line.split("\t")
# return_mat[index, :] = list_from_line[0:3]
# class_label_vector.append(int(list_from_line[-1]))
# index += 1
# 自己编写
for line in array_0_lines:
line = line.strip()
list_from_line = line.split("\t")
# return_mat 存储每一行数据的特征值
return_mat[index, :] = list_from_line[0:3]
# 通过数据的标记做分类
if list_from_line[-1] == "didntLike":
class_label_vector.append(int(1))
elif list_from_line[-1] == "smallDoses":
class_label_vector.append(int(2))
elif list_from_line[-1] == "largeDoses":
class_label_vector.append(int(3))
index += 1
return return_mat, class_label_vector
def scatter_diagram(dating_data_mat, dating_labels, diagram_type=1):
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# windows下配置 font 为中文字体
# font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
# mac下配置 font 为中文字体
font = FontProperties(fname='/System/Library/Fonts/STHeiti Medium.ttc')
# 通过 dating_labels 的索引获取不同分类在矩阵内的行数
index = 0
index_1 = []
index_2 = []
index_3 = []
for i in dating_labels:
if i == 1:
index_1.append(index)
elif i == 2:
index_2.append(index)
elif i == 3:
index_3.append(index)
index += 1
# 对不同分类在矩阵内不同的行数构造每个分类的矩阵
type_1 = dating_data_mat[index_1, :]
type_2 = dating_data_mat[index_2, :]
type_3 = dating_data_mat[index_3, :]
fig = plt.figure()
ax = fig.add_subplot(111) # 就是1行一列一张画布一张图,
if diagram_type == 1:
# 通过对特征0、1比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 1], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 1], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 1], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('玩视频游戏所耗时间百分比', fontproperties=font)
elif diagram_type == 2:
# 通过对特征1、2比较的散点图
type_1 = ax.scatter(type_1[:, 1], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 1], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 1], type_3[:, 2], c='green')
plt.xlabel('玩视频游戏所耗时间百分比', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
elif diagram_type == 3:
# 通过对特征0、2比较的散点图
type_1 = ax.scatter(type_1[:, 0], type_1[:, 2], c='red')
type_2 = ax.scatter(type_2[:, 0], type_2[:, 2], c='blue')
type_3 = ax.scatter(type_3[:, 0], type_3[:, 2], c='green')
plt.xlabel('每年的飞行里程数', fontproperties=font)
plt.ylabel('每周所消费的冰淇淋公升数', fontproperties=font)
plt.legend((type_1, type_2, type_3), ('不喜欢的人', '魅力一般的人', '极具魅力的人'), loc=4, prop=font)
plt.show()
def auto_norm(data_set):
# min(0)使得函数从列中选取最小值,min(1)使得函数从行中选取最小值
min_vals = data_set.min(0)
max_vals = data_set.max(0)
ranges = max_vals - min_vals
# 获取 data_set 的总行数
m = data_set.shape[0]
# 特征值相除
# 相当于公式里的old_value-min
# tile函数相当于将 min_vals 重复 m 行,重复1列
norm_data_set = data_set - tile(min_vals, (m, 1))
# 相当于公式里的(old_value-min)/(max-min)
norm_data_set = norm_data_set / tile(ranges, (m, 1))
return norm_data_set, ranges, min_vals
def dating_class_test():
import os
# 测试样本比率
ho_ratio = 0.20
# 读取文本数据
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
# 对数据归一化特征值处理
norm_mat, ranges, min_vals = auto_norm(dating_data_mat)
m = norm_mat.shape[0]
num_test_vecs = int(m * ho_ratio)
error_count = 0
for i in range(num_test_vecs):
# 因为你的数据本来就是随机的,所以直接选择前20%的数据作为测试数据
classifier_result = classify0(norm_mat[i, :], norm_mat[num_test_vecs:m, :], dating_labels[num_test_vecs:m], 3)
if classifier_result != dating_labels[i]: error_count += 1
# print("the total error rate is: {}".format(error_count / float(num_test_vecs)))
# the total error rate is: 0.08
def matplotlib_run():
import os
group, labels = create_data_set()
classify0([0, 0], group, labels, 3)
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
# 需要画图演示开启
'''
diagram_type = 1, 比较特征(0, 1);
diagram_type = 2, 比较特征(1, 2);
diagram_type = 3, 比较特征(0, 2)
'''
scatter_diagram(dating_data_mat, dating_labels, diagram_type=2)
auto_norm(dating_data_mat)
def classify_person():
import os
result_list = ['讨厌', '有点喜欢', '非常喜欢']
ff_miles = float(input("每年的出行公里数(km)?例如:1000\n"))
percent_tats = float(input("每日玩游戏的时间占比(.%)?例如:10\n"))
ice_cream = float(input("每周消费多少零食(kg)?例如:1\n"))
filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'dating_test_set.txt')
dating_data_mat, dating_labels = file2matrix(filename)
norm_mat, ranges, min_vals = auto_norm(dating_data_mat)
in_arr = array([ff_miles, percent_tats, ice_cream])
classifier_result = classify0((in_arr - min_vals) / ranges, norm_mat, dating_labels, 3)
print("你可能对他/她的印象:\n{}".format(result_list[classifier_result - 1]))
def img2vector(filename):
# 构造一个一行有1024个元素的即 1*1024 的矩阵
return_vect = zeros((1, 1024))
with open(filename, 'r', encoding='utf-8') as fr:
# 读取文件的每一行的所有元素
for i in range(32):
line_str = fr.readline()
# 把文件每一行的所有元素按照顺序写入构造的 1*1024 的零矩阵
for j in range(32):
return_vect[0, 32 * i + j] = int(line_str[j])
return return_vect
def hand_writing_class_test():
import os
# 获取训练集和测试集数据的根路径
training_digits_path = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'digits/trainingDigits')
test_digits_path = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'digits/testDigits')
# 对训练集数据做处理,构造一个 m*1024 的矩阵,m 是训练集数据的个数
hw_labels = []
training_file_list = os.listdir(training_digits_path) # type:list
m = training_file_list.__len__()
training_mat = zeros((m, 1024))
# 对训练集中的单个数据做处理
for i in range(m):
# 取出文件中包含的数字
file_name_str = training_file_list[i] # type:str
file_str = file_name_str.split('.')[0]
class_num_str = int(file_str.split('_')[0])
# 添加标记
hw_labels.append(class_num_str)
# 把该文件中的所有元素构造成 1*1024 的矩阵后存入之前构造的 m*1024 的矩阵中对应的行
training_mat[i, :] = img2vector(os.path.join(training_digits_path, file_name_str))
# 对测试集数据做处理,构造一个 m*1024 的矩阵,m 是测试集数据的个数
test_file_list = os.listdir(test_digits_path)
error_count = 0
m_test = test_file_list.__len__()
# 对测试集中的单个数据做处理
for i in range(m_test):
# 取出文件中包含的数字
file_name_str = test_file_list[i]
file_str = file_name_str.split('.')[0]
class_num_str = int(file_str.split('_')[0])
# 把该文件中的所有元素构造成一个 1*1024 的矩阵
vector_under_test = img2vector(os.path.join(test_digits_path, file_name_str))
# 对刚刚构造的 1*1024 的矩阵进行分类处理判断结果
classifier_result = classify0(vector_under_test, training_mat, hw_labels, 3)
# 对判断错误的计数加 1
if classifier_result != class_num_str: error_count += 1
print("错误率: {}".format(error_count / float(m_test)))
def hand_writing_run():
import os
test_digits_0_13_filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'digits/testDigits/0_13.txt')
img2vector(test_digits_0_13_filename)
hand_writing_class_test()
def img_binaryzation(img_filename):
import os
import numpy as np
from PIL import Image
import pylab
# 修改图片的路径
img_filename = os.path.join(os.path.dirname(os.path.dirname(__file__)), img_filename)
# 调整图片的大小为 32*32px
img = Image.open(img_filename)
out = img.resize((32, 32), Image.ANTIALIAS)
out.save(img_filename)
# RGB 转为二值化图
img = Image.open(img_filename)
lim = img.convert('1')
lim.save(img_filename)
img = Image.open(img_filename)
# 将图像转化为数组并将像素转换到0-1之间
img_ndarray = np.asarray(img, dtype='float64') / 256
# 将图像的矩阵形式转化成一位数组保存到 data 中
data = np.ndarray.flatten(img_ndarray)
# 将一维数组转化成矩阵
a_matrix = np.array(data).reshape(32, 32)
# 将矩阵保存到 txt 文件中转化为二进制0,1存储
img_filename_list = img_filename.split('.') # type:list
img_filename_list[-1] = 'jpg'
txt_filename = '.'.join(img_filename_list)
pylab.savetxt(txt_filename, a_matrix, fmt="%.0f", delimiter='')
# 把 .txt 文件中的0和1调换
with open(txt_filename, 'r') as fr:
data = fr.read()
data = data.replace('1', '2')
data = data.replace('0', '1')
data = data.replace('2', '0')
with open(txt_filename, 'w') as fw:
fw.write(data)
return txt_filename
def hand_writing_test(img_filename):
txt_filename = img_binaryzation(img_filename)
import os
# 获取训练集和测试集数据的根路径
training_digits_path = os.path.join(os.path.dirname(os.path.dirname(__file__)), 'digits/trainingDigits')
# 对训练集数据做处理,构造一个 m*1024 的矩阵,m 是训练集数据的个数
hw_labels = []
training_file_list = os.listdir(training_digits_path) # type:list
m = training_file_list.__len__()
training_mat = zeros((m, 1024))
# 对训练集中的单个数据做处理
for i in range(m):
# 取出文件中包含的数字
file_name_str = training_file_list[i] # type:str
file_str = file_name_str.split('.')[0]
class_num_str = int(file_str.split('_')[0])
# 添加标记
hw_labels.append(class_num_str)
# 把该文件中的所有元素构造成 1*1024 的矩阵后存入之前构造的 m*1024 的矩阵中对应的行
training_mat[i, :] = img2vector(os.path.join(training_digits_path, file_name_str))
# 把该文件中的所有元素构造成一个 1*1024 的矩阵
vector_under_test = img2vector(txt_filename)
# 对刚刚构造的 1*1024 的矩阵进行分类处理判断结果
classifier_result = classify0(vector_under_test, training_mat, hw_labels, 3)
return classifier_result
if __name__ == '__main__':
# matplotlib_run()
# dating_class_test()
# classify_person()
# hand_writing_run()
classifier_result = hand_writing_test(img_filename='2.jpg')
print(classifier_result)
好了,我们已经实现了我们的手写识别系统,恭喜你,完成了第一个算法的学习。
k-近邻算法是分类数据最简单最有效的算法,没有复杂的过程和数学公式,相信通过两个例子同学们对 k-近邻算法有了较为深入的了解。但是细心的同学运行这两个算法的时候已经发现了运行该算法的是非常耗时间的。拿识别手写系统举例,因为该算法需要为每个测试向量做2000次距离计算,每个距离包括了1024个维度浮点运算,总计要执行900次,此外,我们还需要为测试向量准备2MB的存储空间。既然有了问题,作为程序员的我们是一定要去解决的,那么是否存在一种算法减少存储空间和计算时间的开销呢?下一章揭晓答案——决策树。
标签:输入 告诉 爱情 读取文件 sys percent beautiful ade 原理
原文地址:https://www.cnblogs.com/nickchen121/p/10912165.html