SegNet

标签：org   告诉   相互   多次   抽样   round   一模一样   利用   黄色   

Paper link:https://arxiv.org/pdf/1511.00561.pdf

Motivation:为了实际应用，主要是在时间效率和存储空间上做了改进；

Introduction:

(1)Pipeline:

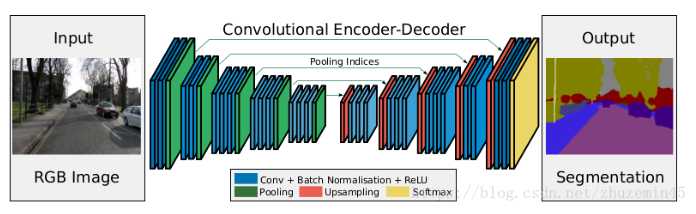
(2)Light

1、带index的pooling:

        在SegNet中的Pooling与其他Pooling多了一个index功能（该文章亮点之一），也就是每次Pooling，都会保存通过max选出的权值在2x2 filter中的相对位置，对于上图的6来说，6在粉色2x2 filter中的位置为(1，1)(index从0开始），黄色的3的index为(0，0)。同时，从网络框架图可以看到绿色的pooling与红色的upsampling通过pool indices相连，实际上是pooling后的indices输出到对应的upsampling（因为网络是对称的，所以第1次的pooling对应最后1次的upsamping，如此类推）。 
        Upsamping就是Pooling的逆过程（index在Upsampling过程中发挥作用），Upsamping使得图片变大2倍。我们清楚的知道Pooling之后，每个filter会丢失了3个权重，这些权重是无法复原的，但是在Upsamping层中可以得到在Pooling中相对Pooling filter的位置。所以Upsampling中先对输入的特征图放大两倍，然后把输入特征图的数据根据Pooling indices放入，下图所示，Unpooling对应上述的Upsampling，switch variables对应Pooling indices。 
如下图：

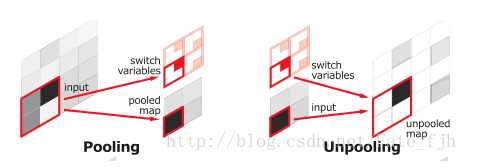
      pooling&Upsampling示意图中右边的Upsampling可以知道，2x2的输入，变成4x4的图，但是除了被记住位置的Pooling indices，其他位置的权值为0，因为数据已经被pooling走了。因此，SegNet使用的反卷积在这里用于填充缺失的内容，因此这里的反卷积与卷积是一模一样，在网络框架图中跟随Upsampling层后面的是也是卷积层。
2、为结果加入置信度（Bayesian SegNet）：

     需要多次采样才能确定一个分布。蒙特卡罗抽样告诉我们可以通过设计一个试验方法将一个事件的频率转化为概率，因为在足够大的样本中，事件发生的频率会趋向事件发生的概率，因此可以很方便地求出一个未知分布。通过蒙特卡罗抽样，就可以求出一个新分布的均值与方差，这样使用方差大小就可以知道一个分布对于样本的差异性，我们知道方差越大差异越大。

     在Bayesian SegNet中通过DropOut层实现多次采样()，多次采样的样本值为最后输出，方差最为其不确定度，方差越大不确定度越大，如图6所示，mean为图像语义分割结果，var为不确定大小。所以在使用Bayesian SegNet预测时，需要多次向前传播采样才能够得到关于分类不确定度的灰度图，Bayesian SegNet预测如下图所示。 

第一行为输入图像，第二行为ground truth，第三行为Bayesian SegNet语义分割输出，第四行为不确定灰度图。可以看到， 
1.对于分类的边界位置，不确定性较大，即其置信度较低。 
2.对于图像语义分割错误的地方，置信度也较低。 
3.对于难以区分的类别，例如人与自行车，road与pavement，两者如果有相互重叠，不确定度会增加。

 （3）Result:

可以达到和FCN相似的效果，但是存储利用率更高；

SegNet

标签：org   告诉   相互   多次   抽样   round   一模一样   利用   黄色   

原文地址：https://www.cnblogs.com/zf-blog/p/10912657.html