标签：记录   array   nlog   stat   length   i++   public   缩小   image   

Brief

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法，是一种插入排序，是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n^2）的第一批算法之一

//插入排序,升序
public static void insertSort(int[] array)
{
    for (int i = 1; i < array.length; ++i)
    {
        int tmp = array[i];
        int j = i;
        while (j - 1 >= 0 && array[j - 1] > tmp)
        {
            array[j] = array[j - 1];
            j--;
        }
        array[j] = tmp;
    }
}

时间复杂度：平均O(nlogn)，最坏(n^2)，最好(n)

基本思想

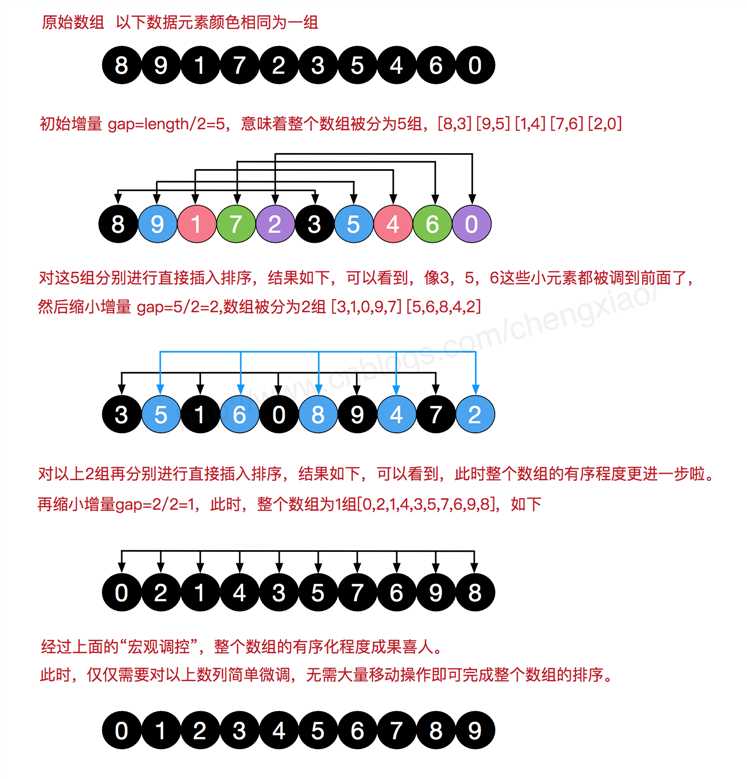
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止

希尔排序的基本步骤，在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2...1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量

希尔排序示例

希尔排序代码

/**
 * 希尔排序 插入时采用移动法
 */
public static void shellSort(int[] arr){
    //增量gap，并逐步缩小增量
    for(int gap = arr.length/2; gap>0; gap/=2){
        //从第gap个元素，逐个对其所在组进行直接插入排序操作
        for(int i = gap; i < arr.length; i++){
            int j = i;
            int tmp = arr[j];
            while(j-gap >= 0 && arr[j-gap] > tmp){
                //移动法
                arr[j] = arr[j-gap];
                j -= gap;
            }
            arr[j] = tmp;
        }
    }
}

希尔排序

标签：记录   array   nlog   stat   length   i++   public   缩小   image   

原文地址：https://www.cnblogs.com/gizing/p/10925262.html