标签:效果 方式 不同 坐标 技术 odi 表示 -o 检查
牛顿的苹果
同学们,你们知道牛顿的苹果的故事吗?
传说1665年秋季,牛顿坐在自家院中的苹果树下苦思着行星绕日运动的原因。这时,一只苹果恰巧落下来,它落在牛顿的脚边。就是这个偶尔的瞬间,牛顿发现了苹果下落的原因——地心引力的作用。
从此,这个苹果被视为科学探索精神的象征。那么,同学们,我们也来探索一下,我们在Scratch中,如何模拟物体的下落?
就像牛顿发现了苹果下落的道理一下,我们需要对于重力的效果进行模拟从而制作出来下落的过程。

对于简单的程序,可使用均速下降的方式。即每隔一段进行将Y坐标增加一个固定的值,就可以了。
对于一些要求比较高的程序,需要使用算法来进行比较准确的模拟。
在重力的作用下运动,一般称为自由落体。根据物理学的知识,物体从0速度开始的自由落体,使用如下的公式进行描述:
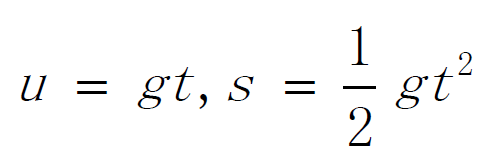
式中的t为时间,一般单位为秒; s为位移(或者说下降的距离)单位为米;u为速度,单位为米/秒; 其中的g为重力加速度,单位为米/秒^2,体现了重力对于自由落体的影响。在不同的星球上,重力加速度的数值是不同的。
在地球上,重力加速度的数值约为9.81米/秒^2,而在月球上,重力加速度的数值约为1.633米/秒^2。所以在月球上,自由落体的下落速度会比地球上慢得多。
我们再对上面的两个公式进行一点深入的解释。
第一个公式表示了自由落体下降速度随时间的变化。也就是“速度=时间*加速度”,所以物体在自由下落的过程中,速度会越来越快,而如果加速度大,则相同时间下速度变化得更大。
速度与时间之间是直线的关系。
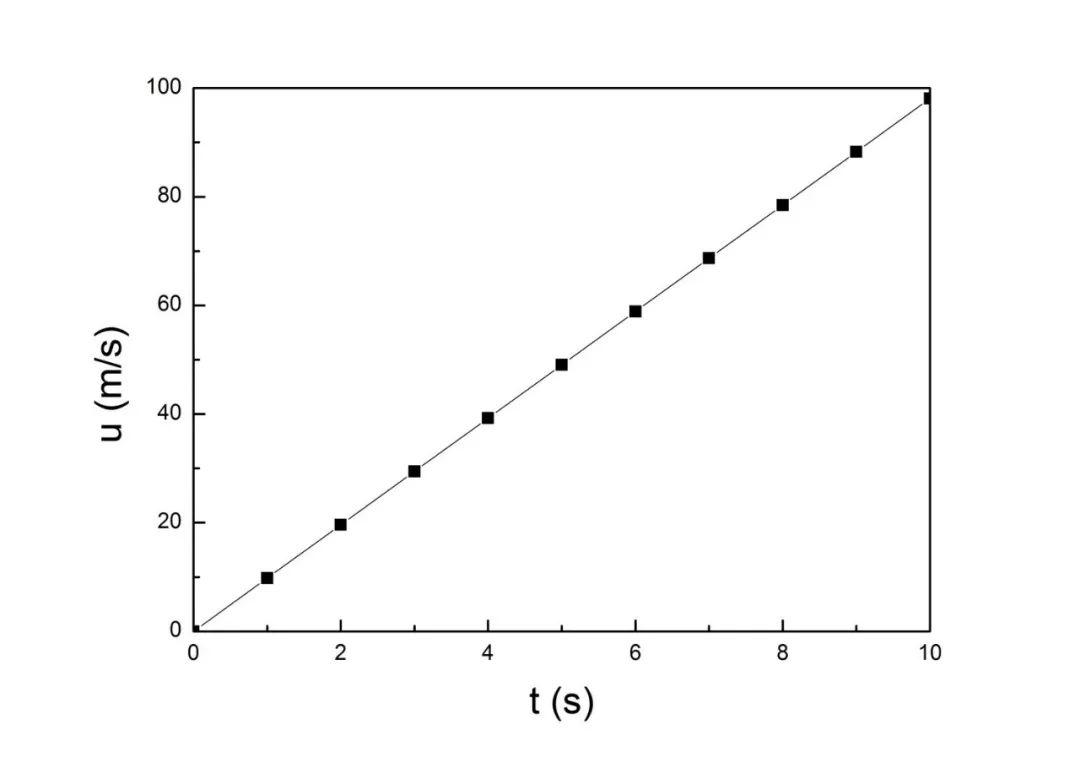
而位移与时间的关系则是一条抛物线,可以看到随时间的增加,位移变化得越来越快。在1秒时,下降了4.9米,而在2秒时,已下降了19.6米。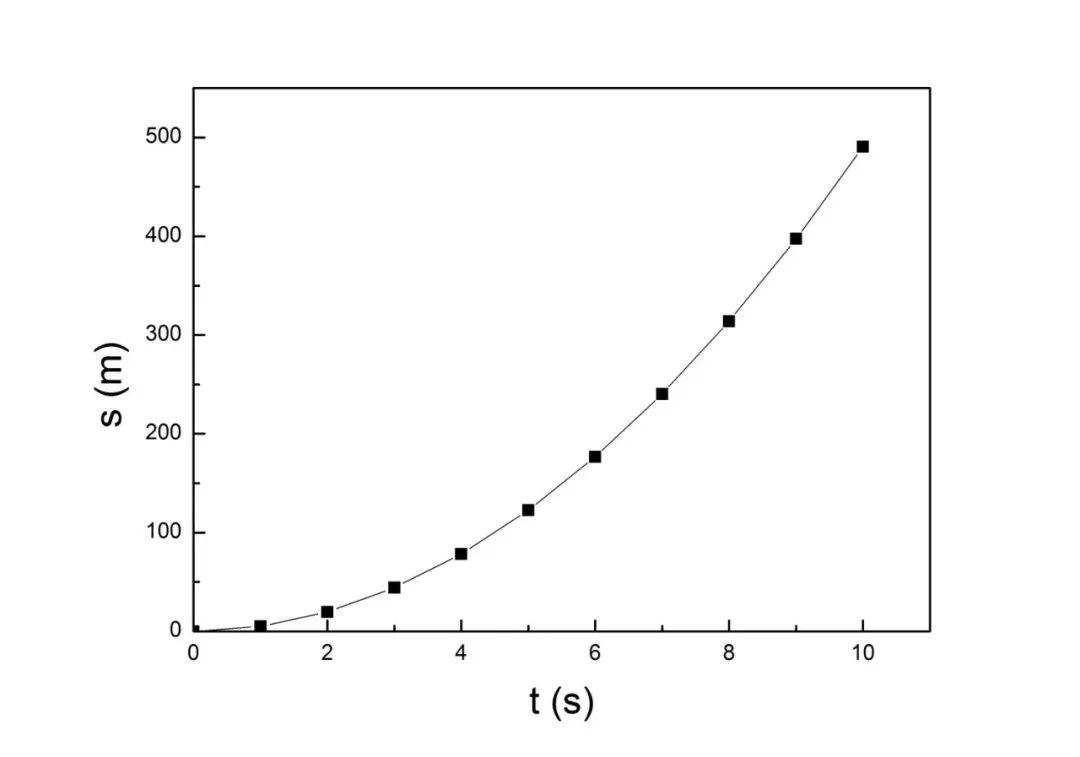
在我们的程序中,应该如何对重力进行模拟呢?
下面我们在Scratch中模拟一个小球的下落,来检查算法的正确性。
基本程序如下,放置一个小球。编写如下的程序。
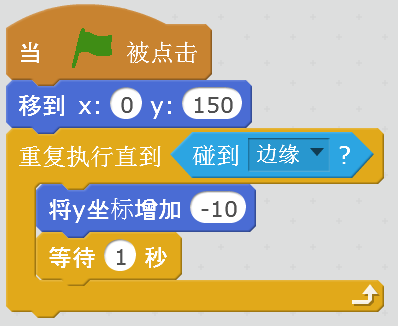
当然,上面这个程序是匀速下降的,下面我们对自由落体的加速过程进行模拟。
方法1:直接使用位移公式

结果如下,可以看到球运动得越来越快。如果改变时间的间隔,能够使得位置变化的更平滑一些。如果改变加速度g,就可以看到下降的速度会增快或减慢。

应该说明,这里直接使用下降的距离作为Y值的变化,即将一个像素当成了1米,可以看到10秒钟下降了397米,即397个像素。
方法2 考虑速度的变化
上面这种方法对于一次下落是很好的,但如果涉及到反弹等的模拟,还是需要考虑速度的变化。
这时使用的公式实际上是在每个时间的间隔Δt时,速度都增加g*Δt,而在同时,位移基本上变化Δt*u。这样就可以比较灵活地对抛物等进行模拟了。例如下面的程序就可以完成弹球的模拟。

其中tstep为时间间隔,xSpeed为X方向运行的速度,0.95表示每次反弹,速度都降为原来的0.95倍(模拟损失了能量)。
效果如下:

可以看到,模拟了自由落体的弹跳。
总结
结论:
1 模拟重力是很多程序中需要使用的功能。
2 根据自由落体的公式,给出了在SCRATCH中模拟自由落体的实现方式。
3 使用自由落体的算法,可以准确地模拟物体的下落过程及弹跳过程等。
4 数学和物理是进行程序模拟的基础,为了更好地对自然界进行模拟,学好数学和物理是必须的。
标签:效果 方式 不同 坐标 技术 odi 表示 -o 检查
原文地址:https://www.cnblogs.com/scratch3/p/10935772.html