标签:就是 function static str 最大 pack 最大的 时间 第一个
算法思想:
从数组中第一个数开始,依次遍历数组中的每一个数,通过相邻比较交换,每一轮循环下来找出剩余未排序数的中的最大数并”冒泡”至数列的顶端。
算法步骤:
(1)从数组中第一个数开始,依次与下一个数比较并次交换比自己小的数,直到最后一个数。如果发生交换,则继续下面的步骤,如果未发生交换,则数组有序,排序结束,此时时间复杂度为O(n);
(2)每一轮”冒泡”结束后,最大的数将出现在乱序数列的最后一位。重复步骤(1)。
稳定性:稳定排序。
时间复杂度: O(n)至O(n2)(function () {。
最好的情况:如果待排序数据序列为正序,则一趟冒泡就可完成排序,排序码的比较次数为n-1次,且没有移动,时间复杂度为O(n)。
最坏的情况:如果待排序数据序列为逆序,则冒泡排序需要n-1次趟起泡,每趟进行n-i次排序码的比较和移动,即比较和移动次数均达到最大值:
比较次数:Cmax=∑i=1n−1(n−i)=n(n−1)/2=O(n2)(this).addClass(′has−numbering′).parent().append(
移动次数等于比较次数,因此最坏时间复杂度为O(n2)。
附代码:
1 package com.wsy; 2 3 public class Sort { 4 public static void main(String[] args) { 5 int[] a = {5,1,6,9,7,3,2,4,8,10}; 6 int temp; 7 int count = 0; 8 // for ( int i =0; i< a.length; i++ ) 9 for ( int i =0; i< a.length-1; i++ ) 10 { 11 // for ( int j =0; j< a.length-1; j++ ) 12 for ( int j =0; j< a.length-1-i; j++ ) 13 { 14 count++; 15 if ( a[j] > a[j+1]) 16 { 17 temp = a[j]; 18 a[j] = a[j+1]; 19 a[j+1] = temp; 20 } 21 } 22 } 23 System.out.println("总共执行了:"+count+"次"); 24 for ( int d : a) 25 { 26 System.out.print(d+" "); 27 } 28 29 } 30 }
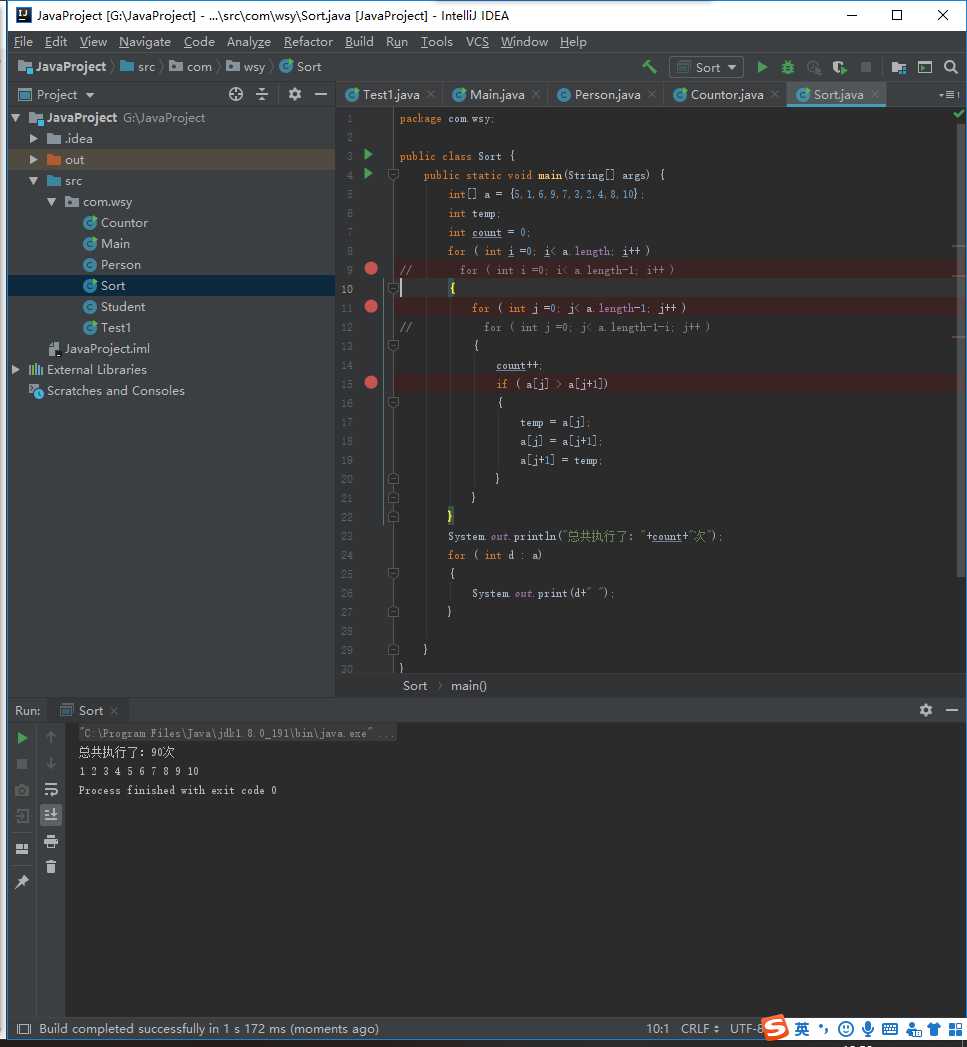
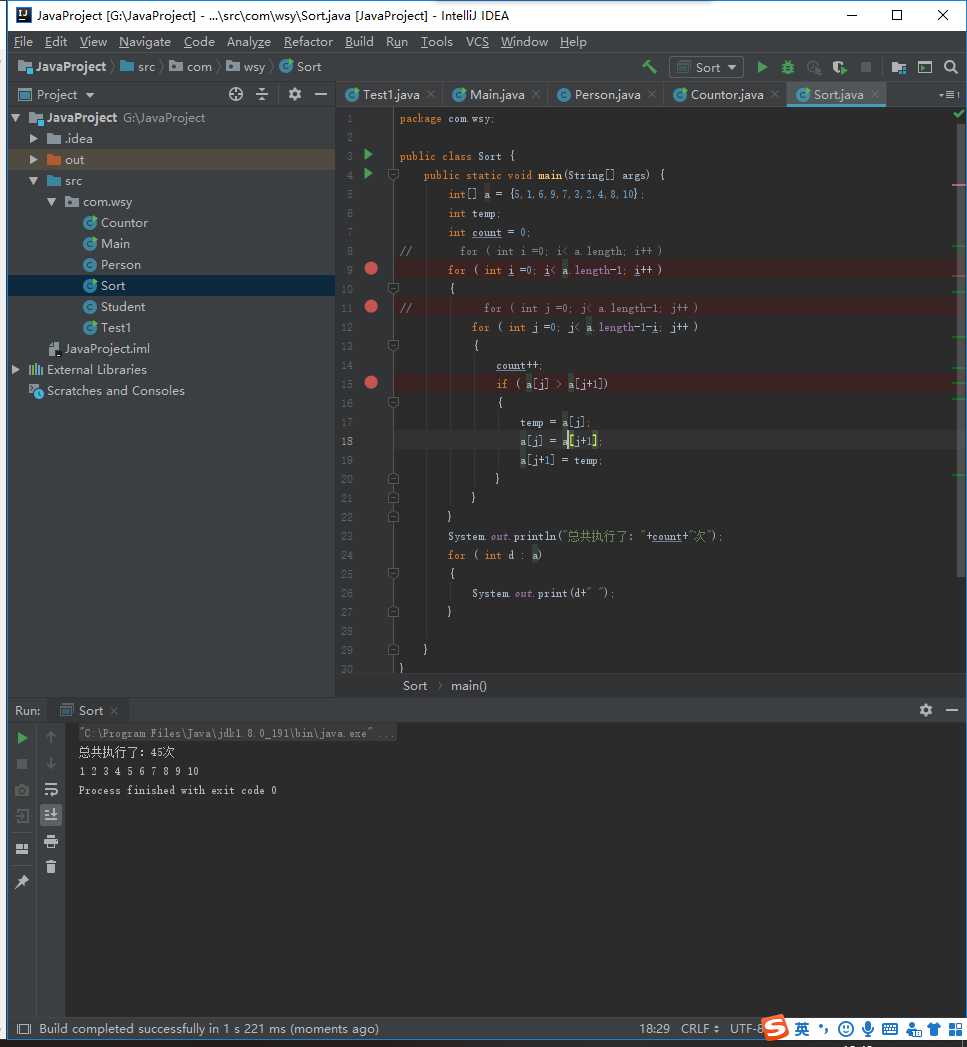
在该段代码中,第一重循环需要控制的是执行的轮次,第二重循环控制的是数据的比对次数,第一重循环每循环一次后,数组的最后一位就是最值,所以再后面的循环中就不需要比对已经是最值的数据了,所以再第二重循环中进行了优化,节省了一半的执行次数,然后想想,在控制的执行轮次,第一重循环循环一次确定一个值得位置,但是最后只剩一个位置的时候就不需要去对比数据了,所以可以少执行循环一次所以第一重循环的次数可以减少一次。以上是我这次对冒泡排序的见解,在高中和大学学习冒泡排序的时候都只是记住代码,记住如何去使用就好了,但是没有去了解冒泡排序的原理,这次通过算法思想和算法步骤把冒泡排序的代码写出来了,但是时间复杂度这个东西好像我已经忘了都,还需要去复习一下。
标签:就是 function static str 最大 pack 最大的 时间 第一个
原文地址:https://www.cnblogs.com/sucker/p/10960597.html