标签:除了 输出 为什么 维度 clu main 很多 题解 算法
动态规划,一种奇妙却苦涩难懂的算法,使若干小白头疼,这次小编会系统的梳理动态规划的基础。
▎什么是动态规划?
一、概念引入
1)动态规划的历史:动态规划最早是在数学领域中使用的,最常见的是在运筹学中的运用,在20世纪50年代初,美国数学家R.E.Bellman等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理。
2)引入 现在思考一个问题:
有面值为1元、2元和5元的硬币若干枚,如何用最少的硬币凑够n元?
首先,我们一定会想到5元硬币面值大(利用贪心的思想),那么一定会优先使用5元硬币,再使用2元的,最后再用1元的,这很符合我们市场买菜时的思路,这么做也没毛病,但是如果硬币面值变了呢?再思考接下来的问题:
有面值为1元、5元和7元的硬币若干枚,如何用最少的硬币凑够n元?
那么这该怎么办?还用刚才的思路吗?显然不行,比如我们要凑出11元,如果用刚才的方法就需要7元*1+1元*4,一共5枚硬币,而实际上只需要3枚硬币(5元*2+1元*1),看来这并不是一种最优的方法,只保证了每次选硬币时当前是最少的,却不能保证整个问题是最优的。这时我们会自然的想到暴力的搜索,但是搜索的时间复杂度往往是指数级的,当n很大时,这种算法就满足不了我们的需求了,这时就要请出动态规划。
二、动态规划的本质
1)继续分析
动态规划没有想象中的复杂,我们不需要仔细思考这选择的整个过程,先来思考最后一枚硬币会是哪一种:显然最后一枚可能是1元的,可能是5元的,也可能是7元的,那么凑n元所需要的硬币数就可能是凑n-1元的硬币数+1(加1枚1元硬币),可能是凑n-5元的硬币数+1(1枚5元硬币),也可能是凑n-7元的硬币数+1(1枚7元硬币)。看到这里,似乎问题还是那么复杂,原来是凑n元,现在却只要知道凑n-1元的硬币数、凑n-5元的硬币数、凑n-7元的硬币数,就知道了凑n元的硬币数。如果原来的凑n枚硬币的规模为n,那么现在要处理的问题规模就是n-1、n-5、n-7,动态规划的本质正是降低问题规模。那么你可能就要问:这谁都能看出来,那么凑n-1元的硬币数、凑n-5元的硬币数、凑n-7元的硬币数又怎么算?这是一个递归(递推也能实现,递归好理解)的过程,比如说我们已经将凑n枚硬币的问题处理成凑n-1、n-5、n-7的问题,我们可以再把n-1,n-5,n-7当做n继续降低规模,直到降低到可以一眼看出来的规模大小,就可以得到这个子问题的答案,在递归回去。文字说不清楚,来个图说明吧:
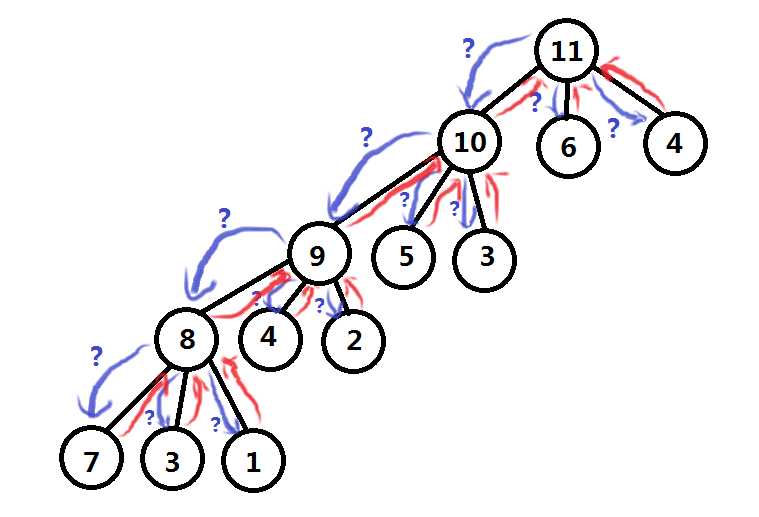
原谅小编粗糙的画技,其中凑1,2,3,4,5,6,7枚硬币我们都可以用肉眼看出来,可以作为边界条件,然后逐个回带就可以了,只要对比每个子问题的值,选出最小的(因为题中说要用最少的硬币),就可以得到原来问题的解。其实动态规划可以理解为经过优化的暴力算法,因为很多时候暴力算法的时间复杂度都会很高,满足不了我们的需求,但暴力算法会有很多冗余的重复计算,所以动态规划的本质也在于去除冗余计算,像上面的硬币问题还可以这用到了降低规模,还可以继续优化,稍后会讲到。
2)总结一下:动态规划就是把大问题分成几个小问题,再继续分解小问题,降低问题规模,去除一些冗余的计算。
3)术语总结:子问题——说白了就是每个问题分解成的小问题,这些小问题对于原来的问题来说就是子问题与问题的关系。
三、三大性质
1)重叠子问题
重叠子问题指的就是原来的问题每次分解的子问题都是相同或相似的,那样原问题就可以尽可能少的调用子问题的结果,那样就可以降低时间复杂度。如果子问题间并不相同或相似,那么动态规划就失去了它的意义,时间复杂度可想而知,还不如用普通的打暴力实在。
2)最优子结构
最优子结构的意思就是说子问题中的最优解就是原问题的最优解,比如说我现在要凑11元,那么凑6元的硬币数+1枚5元硬币就是凑11元的最优的子问题,其中最优子问题:凑6元的方案(5元*1+1元*1)+1枚5元硬币就是原问题:凑11元的方案(5元*2+1元*1)的解.
3)无后效性
无后效性就是说已经决定了的子问题的解将不会再受其他因素改变,比如说我已经知道了凑6元需要2枚硬币,那么将不会再改动,不会再因为凑7元、凑8元、凑9元等发生改变,依旧是两枚硬币。
同时也不会再关心这6元硬币是怎样凑来的,不管我们用了怎样恶毒的手段,怎样卑劣的方法,总之我们知道6元硬币是由2枚硬币凑成的,具体是那两种面值的硬币,我们不会过问。
了解了这些以后,我们在遇到题时,判断一道题能不能动态规划,可以判断这道题是否满足这三大性质,如果满足,就可以放心的动态规划了。
▎状态与转移
1)动态规划的实现形式:动态规划只是一种优化思想,并不是一类代码,所以动态规划的一般实现形式有:递推和递归。(本次先用递归实现)
2)状态&设计状态:状态是一个难点,很多小白(包括小编)都经常犯迷糊,正确的设计状态才是解决一道题的关键。状态可以理解为定义动态规划用到的数组,那么数组里存的是什么呢?这就需要设计,这一过程就可以理解为设计状态。这个数组可以有一维也可以设计更多维度,这些维度所在的下表表示了一些信息。比如刚才的硬币问题,我们就可以定义一个f [ ]数组,那么f [ i ]代表什么意思呢?表示要凑i枚硬币需要用f [ i ]枚硬币,没错,状态就已经设计好了,够简单吧,但是很多题的状态可不是这么容易的。
3)转移&状态转移方程:设计好状态后,就要思考每个状态间的关系,这时有两个方向:1.我从哪里来(递归,这个常用,似乎递推也可以),2.我到哪里去(递推)。比如说刚才的硬币问题,f [11]显然可以用f [4]、f [6]、f [10]中较小的一个刷新它的值(我从哪里来),当然,f [11]也可以用来刷新f [12]、f [16]、f [18]的值(我到哪里去),这个刷新的过程就叫做转移,当然,我们绝对是用我从哪里来居多,后文也会一直用这种思路。有刚才的硬币问题可以得出一个式子:f [n]=min
{f [n-1]+1,f [n-5]+1,f [n-7]+1},像这样的式子叫做状态转移方程,可以理解为状态与状态间的桥梁。正确的设计状态才会使状态转移方程更容易的得到。
▎记忆化搜索VS数组递推
1)记忆化搜索
刚才硬币问题的策略并不是最优的,甚至都算不上是动态规划,只能算是个普通的递归。那么就要优化,采用记忆化的手段,那么记忆化是什么呢?记忆化就是说把已经算好的值保存下来。
为什么要记忆化呢?举个栗子:还是硬币问题,比如说我要调用f [18]时就已经计算过一次f [13]了,而调用f [20]时也要计算f [13],那么f [13]就被重复计算了,如果重复计算的子问题规模很小,那么很快就得到结果了,但是规模一旦大起来了,速度可想而知,如果我们把这些重复计算好的结果都保存起来,那么是不是再调用的时候就可以直接出结果了?
2)数组递推
这种实现方法不会出现重复计算的情况,也避免了函数的调用,但是不好想,之后会具体讲的。
3)对比
记忆化搜索好想好实现,但是时间上除了必要的运算还会有函数调用的时间,所以时间上较慢,却容易实现。
▎硬币问题:记忆化搜索实现
1 #include<iostream> 2 using namespace std; 3 int n,f[1000],a[1000];//设计状态 4 int coin(int i) 5 { 6 if(a[i]!=0) return a[i];//如果算过直接返回 7 if(i==1) return 1; 8 else if(i==2) return 2; 9 else if(i==3) return 3; 10 else if(i==4) return 4; 11 else if(i==5) return 1; 12 else if(i==6) return 2; 13 else if(i==7) return 3; 14 f[i]=min(coin(i-1)+1,min(coin(i-5)+1,coin(i-7)+1));//状态转移方程 15 return a[i]=f[i];//存起来记忆算好的值 16 } 17 int main() 18 { 19 cin>>n; 20 cout<<coin(n); 21 return 0; 22 }
▎难题详解
看完上面简单的硬币问题,接下来就要碾压一下你的心态了,废话不多说,看一道超麻烦的题。
山区建小学
政府在某山区修建了一条道路,恰好穿越总共m个村庄的每个村庄一次,没有回路或交叉,任意两个村庄只能通过这条路来往。已知任意两个相邻的村庄之间的距离为di(为正整数),其中,0<i<m。为了提高山区的文化素质,政府又决定从m个村中选择n个村建小学(设0<n≤m<500)。请根据给定的m、n以及所有相邻村庄的距离,选择在哪些村庄建小学,才使得所有村到最近小学的距离总和最小,计算最小值。
第1行为m和n,其间用空格间隔
第2行为m?1 个整数,依次表示从一端到另一端的相邻村庄的距离,整数之间以空格间隔。
例如:
10 3 2 4 6 5 2 4 3 1 3
表示在10个村庄建3所学校。第1个村庄与第2个村庄距离为2,第2个村庄与第3个村庄距离为4,第3个村庄与第4个村庄距离为6,...,第9个村庄到第10个村庄的距离为3。
各村庄到最近学校的距离之和的最小值。
10 2 3 1 3 1 1 1 1 1 3
18
这道题太麻烦,感觉写到一篇博客里慌得不行。
发一下之前小编写过的题解:山区建小学。
标签:除了 输出 为什么 维度 clu main 很多 题解 算法
原文地址:https://www.cnblogs.com/TFLS-gzr/p/10962216.html