标签：要求 $0 去掉 很多 smo cli 定义 src set
前段时间准备执业医、师兄师姐答辩拍照、找实习。博客又落下了。继续继续ing~
紧接上一节SVM，来讲SMO，SMO为SVM最难啃的地方了吧，看到一大推公式。
我本着省去最繁琐的公式推导，给大家尽可能用人话讲清SMO的道理。
首先，上一节，我们得到最后的优化目标：
$\underset{a}{min}=\frac{1}{2}\sum \sum a_{i}a_{j}y_{i}y_{j}\mathbf{K}（x_{i}，x_{j}）-\sum a_{i}$
$s.t \sum a_{i}y_{i}=0$
$0\leqslant \alpha _{i}\leqslant C$
现在就补了这个坑。
SMO只一次优化两个未知参数$\alpha _{1}$ ,$\alpha _{2}$，将其他$\alpha _{i＞2}$共N-2个参数固定，将原始求解N个参数二次规划问题分解成很多个子二次规划问题分别求解，每个子问题只需要求解2个参数，方法类似于坐标上升。
首先根据约束条件$ \sum a_{i}y_{i}=0$，固定$\alpha _{1}$ ,$\alpha _{2}$，其他参数当成常数。
有
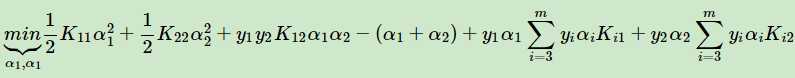（i和j分别取1,2，但是核函数里只有j可动，i已知，不可动）（0）
根据约束条件有$\alpha _{1}y_{1}+ \alpha _{2}y_{2}=-\sum _{j=3}^{N}y_{j}=\zeta $（1）
由（1）得
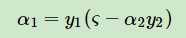（等式两边同乘以y1，且$y_{i}^{2}=1$）（2）
且假设我们上一轮迭代得到$\alpha _{1}^{old}$,$\alpha _{2}^{old}$，以及下轮迭代得到的$\alpha _{1}^{new}$，$\alpha _{1}^{new}$
定义一个函数，为了后面简化公式（类似于损失函数，把超平面g(x)当做预测值，yi当做真实值）
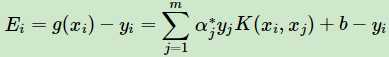（3）
令
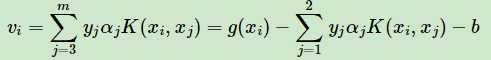（同样为了简化公式）（相当于超平面g(x)去掉$\alpha _{1}$ ,$\alpha _{2}$的部分）（4）
准备工作做完了，我说的简化公式计算就在这。（假设先求α2，由公式2可求得α1）将公式2,3,4带入公式0中，有
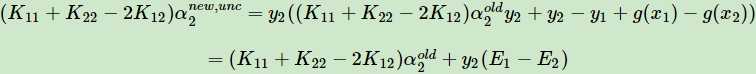
得到$\alpha _{2}^{new，unclipped}$
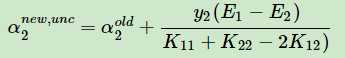
tips
到这，大家有疑问了，这个什么未修剪的$\alpha _{2}$什么鬼？
其实就是不加约束条件的下，直接求出来的 $\alpha _{2}$嘛。
下面加上约束条件。
根据约束条件可得公式1和$0\leqslant \alpha _{i}\leqslant C$
大家可以手动设定$\alpha _{1}y_{1}+ \alpha _{2}y_{2}=-\sum _{j=3}^{N}y_{j}=\zeta $（1）等于比如3，C=5，y1≠y2
下图是博主本人手算的，对于理解SMO原文中图a很有帮助
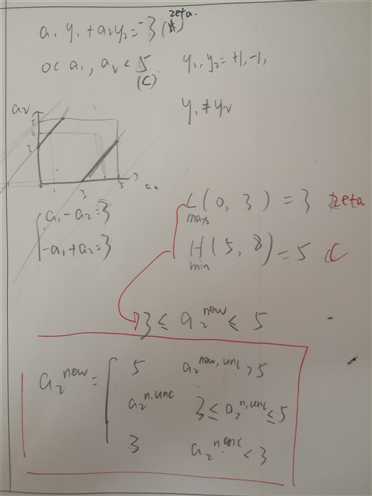
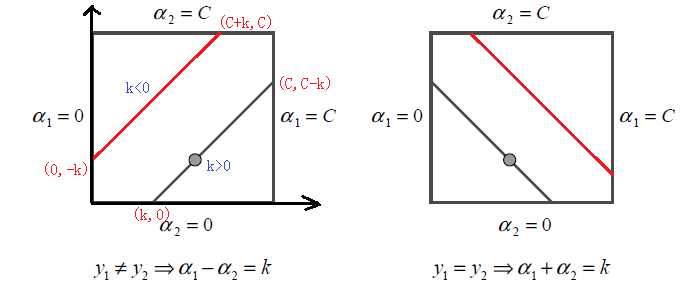（a）
当为上图左图，有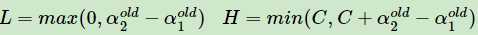
当为上图右图，有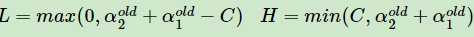
最后有$\alpha _{2}^{new，unclipped}$和$\alpha _{2}^{new}$的关系为
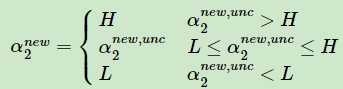
到此，我们再总结一下，把优化目标里的a1，a2看最未知，其他a都已知
通过对优化目标的求导，化简，变形等，求出$\alpha _{2}^{new，unclipped}$
再根据约束条件，得到$\alpha _{2}^{new，unclipped}$和$\alpha _{2}^{new}$的关系，即得到了$\alpha _{2}^{new}$
再根据公式1，得到$\alpha _{1}^{new}$。
参考：
https://www.cnblogs.com/pinard/p/6111471.html
https://blog.csdn.net/luoshixian099/article/details/51227754
支持向量机课（SVM）（五）--SMO算法（省去公式推导，只讲其思想）
标签：要求 $0 去掉 很多 smo cli 定义 src set
原文地址：https://www.cnblogs.com/super-yb/p/10966484.html
