标签:bec art alc section normal signal href 状态 roc
搬运自我的CSDN https://blog.csdn.net/u013213111/article/details/90529164
参考:
双二阶滤波器
本文中的例子和代码放在Github
First,什么是双二阶滤波器?wiki上是这么说的:二阶、递归、线性,含有两个极点和两个零点,“双二阶”的名字来源于它的传递函数是两个二次多项式的比值。
In signal processing, a digital biquad filter is a second order recursive linear filter, containing two poles and two zeros. "Biquad" is an abbreviation of "biquadratic", which refers to the fact that in the Z domain, its transfer function is the ratio of two quadratic functions: H(z)=(b?+b?z?1+b?z?2)/(a?+a?z?1+a?z?2) The coefficients are often normalized such that a? = 1: H(z)=(b?+b?z?1+b?z?2)/(1+a?z?1+a?z?2) High-order IIR filters can be highly sensitive to quantization of their coefficients, and can easily become unstable.
归一化传递函数写成这样:
H(z)=(b?+b?z?1+b?z?2)/(1+a?z?1+a?z?2)
用MATLAB的Filter Designer来设计一个:400Hz带通IIR,需要用4个Sections来实现,默认给出的滤波器结构是Direct-Form II。
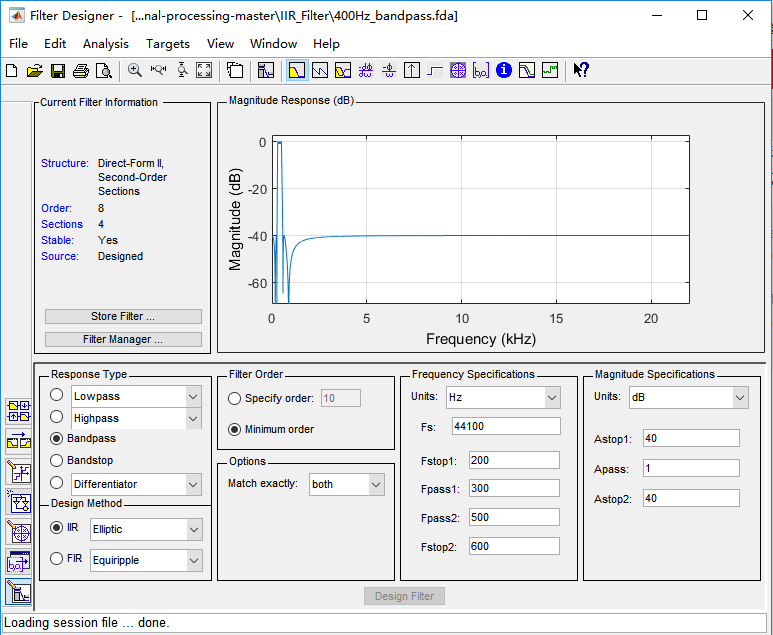
在菜单栏的Analysis中选择Filter Coeffients就能看到滤波器系数了:
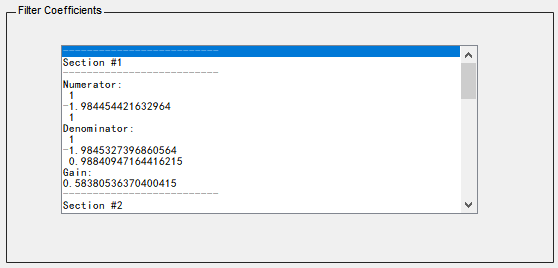
Numerator,分子,也就是传递函数中的b项们,从上到下依次为b?,b?和b?。
Denominator,分母,也就是传递函数中的a项,从上到下依次为a?,a?和a?,其中a?总是为1。
Gain,增益。
用数组来存放滤波器系数:
//8-order IIR filter with 4 sections
const int sections = 4;
//nominator
const float b[4][3] = {
{ 1, -1.984454421, 1 },
{ 1, -1.999405318, 1 },
{ 1, -1.993167556, 1 },
{ 1, -1.998644244, 1 }
};
//denominator
const float a[4][3] = {
{ 1, -1.984532740, 0.9884094716 },
{ 1, -1.988571923, 0.9909378613 },
{ 1, -1.991214225, 0.9962624248 },
{ 1, -1.995917854, 0.9977478940 }
};
const float gain[4] = { 0.583805364, 0.583805364, 0.170388576, 0.170388576 };以Direct-Form II为例来写个实现代码,计算过程是:
y[n]=b?w[n]+b?w[n-1]+b?w[n-2]
其中w[n]=x[n]-a?w[n-1]-a?w[n-2]
代码如下:
用一个数组来存放滤波器的中间状态量w[n-1]和w[n-2]:
float w[sections][2]; //filter states在滤波计算之前,初始化滤波器:
for (int i = 0; i < sections; i++) {
w[i][0] = 0; //w[n-1]
w[i][1] = 0; //w[n-2]
}正式开始计算:pcmIn[i]是原始的输入信号,输入section 1,section 1的输出则作为section 2的输入,以此类推,由于这个滤波器由4个sections构成,因此要循环4次。
注意输出要乘gain。
y[0] = pcmIn[i];
for (j = 0; j < sections; j++) {
tmp[j] = y[j] - a[j][1] * w[j][0] - a[j][2] * w[j][1]; //calculate w[n]
y[j+1] = tmp[j] + b[j][1] * w[j][0] + b[j][2] * w[j][1]; //calculate the j-th section filter output y[n]
w[j][1] = w[j][0]; //move w[n-1] -> w[n-2]
w[j][0] = tmp[j]; //move w[n] -> w[n-1]
y[j+1] = gain[j] * y[j+1]; //multiply with gain
}
out = y[j];如果需要得到例如PCM16的输出,那么再对out进行限幅,that‘s all.
标签:bec art alc section normal signal href 状态 roc
原文地址:https://www.cnblogs.com/lyrich/p/10987875.html