标签:对象 有向图 大于 names cstring scanf return amp map
Dijstra算法代码借鉴:
#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #define Inf 0x3f3f3f3f using namespace std; int map[1005][1005];//存储输入数组值 int vis[1005],dis[1005];//vis标记数组,dis最短路径 int n,m;//n个点,m条边 void Init () { memset(map,Inf,sizeof(map));//初始化map数组 for(int i=1;i<=n;i++) { map[i][i]=0; }//将该节点到该节点的权值置0,即数组斜线上的值置0 } void Getmap() { int u,v,w; for(int t=1;t<=m;t++) { scanf("%d%d%d",&u,&v,&w);//输入数组行列下标及该点的权值 if(map[u][v]>w)//如果初始化的map[][]数组值(init函数置无穷大)大于 当前输入的权值 { map[u][v]=w; map[v][u]=w; } } } void Dijkstra(int u)//对结点进行操作 { memset(vis,0,sizeof(vis));//vis数组清空 for(int t=1;t<=n;t++) { dis[t]=map[u][t];//从map第一列开始将值存到dis数组中,dis数组存放最短路径权值 } vis[u]=1;//将vis数组置的n结点权值为1 ,标记数组,代表已经访问过 //两重for循环找最短路径 for(int t=1;t<n;t++) { int minn=Inf,temp;//定义变量min为无穷大 for(int i=1;i<=n;i++) { if(!vis[i]&&dis[i]<minn)//没有访问过该节点,且存放最短路径的dis数组在该点权值小于minn { minn=dis[i];//将dis数组在该点的权值更新到minn变量中保存 temp=i;//更新数组下标 } } vis[temp]=1;//标记已访问过该点 for(int i=1;i<=n;i++) { if(map[temp][i]+dis[temp]<dis[i])//如果当前结点的权值+存放在最短路径的当前结点的权值累加和 小于 前一个结点的权值 { dis[i]=map[temp][i]+dis[temp];//则更新前一个结点的权值 } } } } int main() { scanf("%d%d",&m,&n); Init(); Getmap(); Dijkstra(n); printf("%d\n",dis[1]);//打印数组下标为1到其他点的单源最短路径 return 0; }
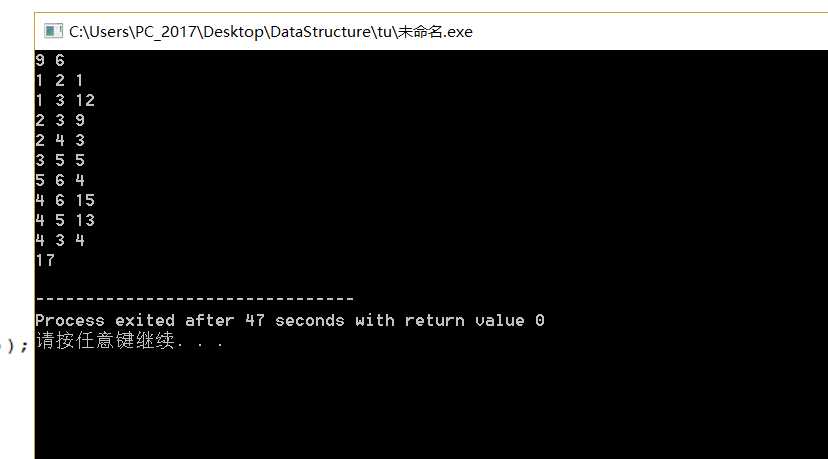
Dijkstra算法的主要思路:
map初始化数组,vis标记数组,dis存放最短路径长度
核心代码:
for(int t=1;t<n;t++) { int minn=Inf,temp;//定义变量min为无穷大 for(int i=1;i<=n;i++) { if(!vis[i]&&dis[i]<minn)//没有访问过该节点,且存放最短路径的dis数组在该点权值小于minn { minn=dis[i];//将dis数组在该点的权值更新到minn变量中保存 temp=i;//更新数组下标 } } vis[temp]=1;//标记已访问过该点 for(int i=1;i<=n;i++) { if(map[temp][i]+dis[temp]<dis[i])//如果当前结点的权值+存放在最短路径的当前结点的权值累加和 小于 前一个结点的权值 { dis[i]=map[temp][i]+dis[temp];//则更新前一个结点的权值 } } }
类似于prime算法, Dijkstra算法的对象无所谓是有向图还是无向图,它可以求单源最短路径(一个点到其余各点的最短路径),时间复杂度为O(n*n)。
区别:
核心思想就是更新连接路径时,prime中是跟踪接下来的结点到生成树中的最小交叉边,而dijkstra中是跟踪接下来的结点到
起点所有经过的结点的路径和。
标签:对象 有向图 大于 names cstring scanf return amp map
原文地址:https://www.cnblogs.com/javabai/p/10988842.html