数据结构和算法-最短路径

标签：广度优先   最短路径算法   ima   heap   lock   最小   tar   not   时间   

针对无权图可以使用深度优先和广度优先算法, 有权图可以使用最短路径算法

Dijkstra(迪杰斯特拉算法): 在有向加权图中查找最短路径

注意: 该算法只适用于有向无环图, 不适用于负权边的情况

思路:

1. 找出距离起点最近的节点
2. 对于该节点邻居, 检查是否有前往他们的更短路径, 如果有就更新开销
3. 重复以上两步, 直到所有节点运行过
4. 找出最短路径

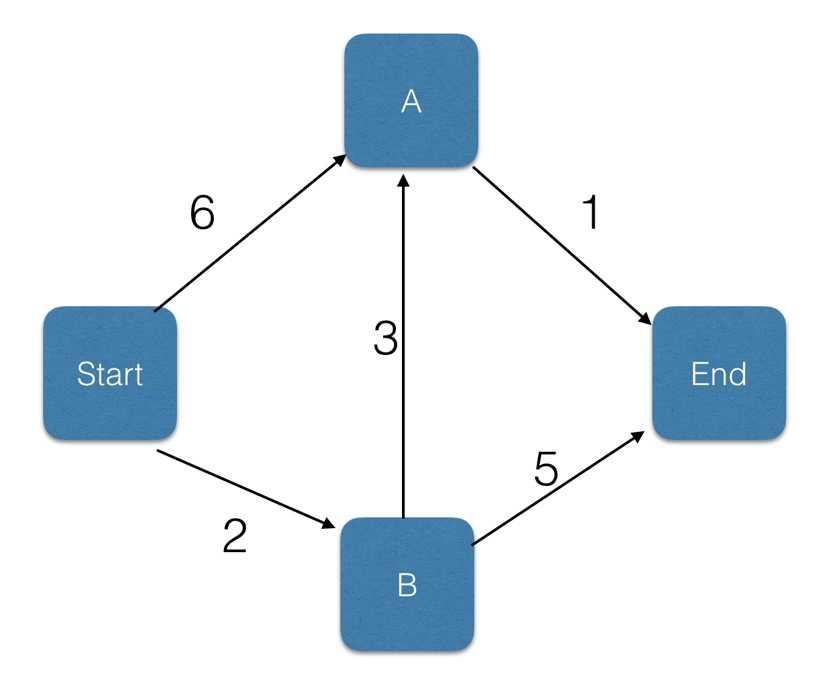
下表为要从起点到达终点, 数字为花费的时间

上图是按照以上步骤进行填充的

1. 找出start的邻居节点A和B, 其中B的花费最少
2. 找出B节点的邻居节点A和end, 更新到A节点的开销
3. 继续对A节点进行, 从A到end花费最小, 更新B到end的开销

所以最小距离为start --> B --> A --> end

实现

利用最小堆实现, 时间复杂度: O(e * logv), e是边的个数

# -*- coding:utf-8 -*-

'''
Dijkstra算法(最短路径算法)

- 适用于有向有权无环图
- 不适用于负权边的情况
'''

import heapq


class Graph(object):
    def __init__(self):
        self.graph = {}

    def add_edge(self, start: str, end: str, distance: float):
        self.graph.setdefault(start, {})
        self.graph[start][end] = distance


def dijkstra(start: str, end: str, graph: dict) -> list:
    visited = set()  # 存储已经处理过的节点
    costs = {start: 0}

    queue = [(0, start)]
    path = {}  # 用于复原路径

    while queue:
        dis, min_node = heapq.heappop(queue)
        if min_node == end:
            break

        if min_node not in visited:
            visited.add(min_node)

            neighbors = graph[min_node]
            for i, j in neighbors.items():
                new_dis = dis + j
                if (i not in costs) or (new_dis < costs[i]):
                    costs[i] = new_dis
                    heapq.heappush(queue, (new_dis, i))
                    path[i] = min_node

    res = []
    key = end
    while key != start:
        res.append(key)
        key = path[key]
    res.append(start)
    res.reverse()

    return res


if __name__ == '__main__':
    g1 = Graph()
    g1.add_edge('start', 'a', 3)
    g1.add_edge('start', 'b', 2)
    g1.add_edge('b', 'a', 6)
    g1.add_edge('b', 'end', 5)
    g1.add_edge('a', 'end', 1)
    assert dijkstra('start', 'end', g1.graph) == ['start', 'a', 'end']

    g2 = Graph()
    g2.add_edge('start', 'a', 5)
    g2.add_edge('start', 'b', 2)
    g2.add_edge('b', 'a', 1)
    g2.add_edge('b', 'end', 5)
    g2.add_edge('a', 'end', 1)
    assert dijkstra('start', 'end', g2.graph) == ['start', 'b', 'a', 'end']

• 利用最小堆不断找出开销最小的节点
• 当发现有到达某个节点的更短距离是更新该节点的距离

资料

• <<漫画算法>>
• <<数据结构和算法>>

数据结构和算法-最短路径

标签：广度优先   最短路径算法   ima   heap   lock   最小   tar   not   时间   

原文地址：https://www.cnblogs.com/zlone/p/11013606.html