标签:一个 col public 可能性 stat 递归 void i++ 深度
全排列是指n个数(或其他字符)所有可能的排列顺序,例如1 2 3三个数字的全排列是
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
那么问题来了,任意输入一个大于1的数字n,列出1-n这n个数字的全排列。
如果尝试手动列举一下1 2 3的全排列,会发现通常我们会在头脑中制定好规则,并按照既定规则进行枚举,从而得到所有排列。
在这里我们制定的规则是:
(想象我们手里拿了3个数字,地上有A、B、C三个空位)
1)在每一个空位前,都按照1->2->3的顺序尝试放下一个数字,如果该数字已经放下则尝试下一个
2)每放下一个数字后向后移动一格,然后重复1->2->3的尝试
3)如果当前位置没有新的可能性,取回当前位置的数字并左移一格从新尝试
按上面规则很容易推算出第一种排列是1 2 3
取回3,返回B位置,取回2,然后按1->2->3尝试,发现可以放下3,右移到C,尝试后放下2,得到1 3 2
接下来必须返回到A的位置才有新的可能性,此时已经取回所有数字,按规则放下2,移到B,放下1,移到C,放下3,得到2 1 3
。。。
下面来看实现的代码:
public class Permutation { private int max; private int[] array; private int[] hold; public Permutation(int max) { this.max = max; array = new int[max + 1]; hold = new int[max + 1]; } public void permute(int step) { if(step == max + 1) { for(int i = 1; i <= max; i++) { System.out.print(array[i] + " "); } System.out.println(); return; //返回上一步, 即最近一次调用permute方法的后一行 } //按照1->2->3->...->n的顺序尝试 for(int num = 1; num <= max; num++) { //判断是否还持有该数字 if(hold[num] == 0) { array[step] = num; hold[num] = 1; //递归: 右移一格重复遍历数字的尝试 permute(step + 1); //回到当前位置时取回当前位置数字 hold[num] = 0; } } } public static void main(String[] args) { Permutation fa = new Permutation(3); fa.permute(1); } }
运行输出
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
我们用一个伪时序图来帮助理解递归调用的执行过程
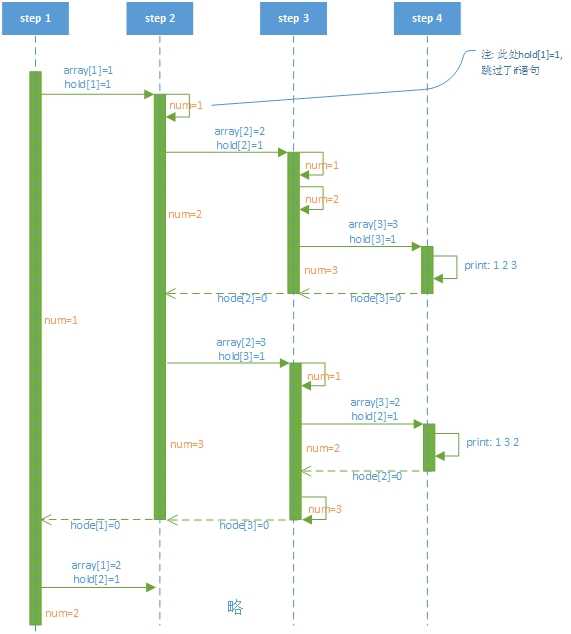
顺便说一句,全排列问题还有多种算法,本文中使用的是深度优先算法的模型。
---------------------
原文:https://blog.csdn.net/autfish/article/details/52385253
标签:一个 col public 可能性 stat 递归 void i++ 深度
原文地址:https://www.cnblogs.com/xiaoshen666/p/11059764.html