标签:long fibonacci 理想 image join 1年 || compute div
斐波那契数列问题:如果一对兔子每月能生1对小兔子,而每对小兔在它出生后的第三个月里,又能开始生1对小兔子,假定在不发生死亡的情况下,由一对初生的兔子开始,1年后能繁殖出多少对兔子?
首先手工计算来总结规律,如下表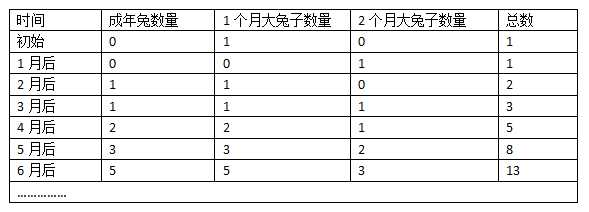
注意总数这一列
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
可以得出规律,第n个斐波那契数=第n-1个斐波那契数+第n-2个斐波那契数
为了计算n,必须计算n-1和n-2;为了计算n-1,必须计算n-2和n-3;直到n-x的值为1为止,这显示是递归大显身手的地方。来看代码
public class Fibonacci { public static long calc(long n) { if(n < 0) { return 0; } if(n == 0 || n == 1) { return n; } else { return calc(n - 1) + calc(n - 2); } } }
这真是极短的,测试代码
public static void main(String[] args) { long n = 50; long begin = System.nanoTime(); long f = Fibonacci.calc(n); long end = System.nanoTime(); System.out.println("第" + n + "个斐波那契数是" + f + ", 耗时" + TimeUnit.NANOSECONDS.toMillis(end - begin) + "毫秒"); }
运行输出
第50个斐波那契数是12586269025, 耗时66024毫秒
注意看消耗的时间,在我的电脑上耗时66秒,真是个相当耗时的操作。既然整个过程都是在不断重复相同的计算规则,那我们可以采用分而治之的思想来优化代码。
import java.util.concurrent.ForkJoinPool; import java.util.concurrent.RecursiveTask; import java.util.concurrent.TimeUnit; public class Fibonacci extends RecursiveTask<Long> { long n; public Fibonacci(long n) { this.n = n; } public Long compute() { if(n <= 10) { //小于10不再分解 return Fibonacci.calc(n); } Fibonacci f1 = new Fibonacci(n - 1); //分解出计算n-1斐波那契数的子任务 f1.fork(); //由ForkJoinPool分配线程执行子任务 Fibonacci f2 = new Fibonacci(n - 2); //分解出计算n-2斐波那契数的子任务 return f2.compute() + f1.join(); } public static long calc(long n) { if(n < 0) { return 0; } if(n == 0 || n == 1) { return n; } else { return calc(n - 1) + calc(n - 2); } } public static void main(String[] args) { long n = 50; long begin = System.nanoTime(); Fibonacci fibonacci = new Fibonacci(n); ForkJoinPool pool = new ForkJoinPool(); long f = pool.invoke(fibonacci); long end = System.nanoTime(); System.out.println("第" + n + "个斐波那契数是" + f + ", 耗时" + TimeUnit.NANOSECONDS.toMillis(end - begin) + "毫秒"); } }
运行输出
第50个斐波那契数是12586269025, 耗时20461毫秒
虽然时间缩短了2/3,但是仍然不理想。回头重新看计算方法,用递归方式虽然代码简短,但是存在很严重的重复计算,下面用非递归的方式改写,过程中每个数只计算一次。
public static long calcWithoutRecursion(long n) { if(n < 0) return 0; if(n == 0 || n == 1) { return n; } long fib = 0; long fibOne = 1; long fibTwo = 1; for(long i = 2; i < n; i++) { fib = fibOne + fibTwo; fibTwo = fibOne; fibOne = fib; } return fib; }
测试
第50个斐波那契数是12586269025, 耗时0毫秒
斐波那契数的另一个经典题目是青蛙跳台阶问题:
一只青蛙一次可以条一级或两级台阶,求该青蛙跳上n级的台阶共有多少种跳法。
假设计算第n级台阶跳法的函数是f(n),当n>2时,第一步选择跳一级有X种跳法,第一步选择跳两级有Y种跳法,f(n)=X+Y。如何计算X呢,站在青蛙的位置考虑,面对的是一个全新的n-1级台阶,有f(n-1)种跳法,那么Y就是n-2级台阶的跳法,那么f(n)=f(n-1)+f(n-2),即斐波那契数列公式。
---------------------
原文:https://blog.csdn.net/autfish/article/details/52370830
标签:long fibonacci 理想 image join 1年 || compute div
原文地址:https://www.cnblogs.com/xiaoshen666/p/11059602.html