标签:完全 gem printf ddl orm quic 区域 解析 函数
一、基本概念
分治法,顾名思义,即分而治之的算法,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……
二、基本思想及策略
设计思想:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
策略:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
三、分治法适用的情况
分治法所能解决的问题一般具有以下几个特征:
1) 该问题的规模缩小到一定的程度就可以容易地解决
2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解;
4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
第一条特征是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加;
第二条特征是应用分治法的前提它也是大多数问题可以满足的,此特征反映了递归思想的应用;、
第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法。
第四条特征涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
四、分治法的基本步骤
分治法在每一层递归上都有三个步骤:
五、(一)分治法之二分搜索
算法概述:二分搜索算法,也称折半查找算法,即在一个有序数组中查找某一个特定元素。整个搜索过程从中间开始,如果要查找的元素即中间元素,那么搜索过程结束;反之根据中间元素与要查找元素的关系在数组对应的那一半查找,例如查找元素大于中间元素,则在整个数组较大元素的那一半查找,反复进行这个过程,直到找到元素,或者数组为空,查找不到元素。
A_0,A_1...A_{n-1}, A_0 \le A_1 \le \cdot \le A_{n - 1},待查找元素为searchnum:left,right分别表示左右端点,即要查找的范围;middle表示中间点,middle = \lfloor (left + right) / 2 \rfloor;left > right,搜索失败;A{middle} > searchnum,right = middle - 1,返回3;A{middle} < searchnum,left = middle + 1,返回3;A{middle} = searchnum,搜索结束,返回middle。
动态演示【low表示左端点,high表示右端点】
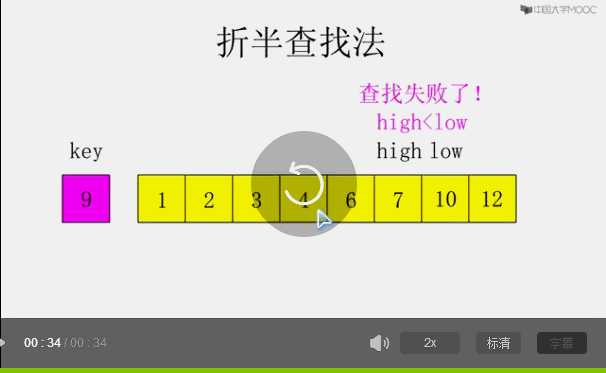
代码实现
不使用递归求解
int binarySearch(arrType * a, arrType searchnum, int left, int right) { int middle; while (left <= right) { middle = (left + right) / 2; if (a[middle] > searchnum) right = middle - 1; else if (a[middle] < searchnum) left = middle + 1; else if (a[middle] == searchnum) return middle; } return -1; }
使用递归求解
int binarySearch(arrType * a, arrType searchnum, int left, int right) { int middle; if (left <= right) { middle = (left + right) / 2; if (a[middle] > searchnum) return binarySearch(a, searchnum, left, middle - 1); else if (a[middle] < searchnum) return binarySearch(a, searchnum, middle + 1, right); else if (a[middle] == searchnum) return middle; } return -1; }
五、(二)分治法之棋盘覆盖
问题描述:在一个2^k×2^k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘.显然特殊方格在棋盘上出现的位置有4^k种情形.因而对任何k≥0,有4^k种不同的特殊棋盘.
下图中的特殊棋盘是当k=3时64个特殊棋盘中的一个:k = 3,棋盘大小8 x 8
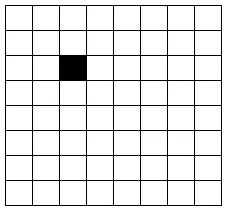
在棋盘覆盖问题中,要用下图中 4 中不同形态的** L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖**。易知,在任何一个 2^k × 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。
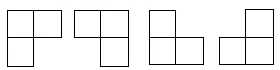
用分治策略,可以设计解棋盘问题的一个简捷的算法
当 k>0 时,将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘,如下图所示:四个子棋盘

特殊方格必位于 4 个较小子棋盘之一中,其余 3 个子棋盘中无特殊方格。
为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘,我们可以用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处,如下图所示,这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题化为 4 个较小规模的棋盘覆盖问题。
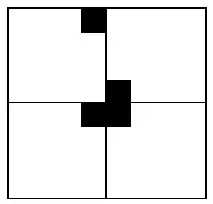
递归的使用这种分割,直至棋盘简化为 1x1 棋盘。
代码实现
#include <stdio.h> #define BOARD_SIZE 4 int board[BOARD_SIZE][BOARD_SIZE]; // c1, r1: 棋盘左上角的行号和列号 // c2, r2: 特殊方格的行号和列号 // size = 2 ^ k void chessboard(int r1, int c1, int r2, int c2, int size) { if(1 == size) return; int half_size; static int domino_num = 1; int d = domino_num++; half_size = size / 2; if(r2 < r1 + half_size && c2 < c1 + half_size) //特殊方格在左上角子棋盘 { chessboard(r1, c1, r2, c2, half_size); } else // 不在此棋盘,将此棋盘右下角设为相应的骨牌号 { board[r1 + half_size - 1][c1 + half_size - 1] = d; chessboard(r1, c1, r1 + half_size - 1, c1 + half_size - 1, half_size); } if(r2 < r1 + half_size && c2 >= c1 + half_size) //特殊方格在右上角子棋盘 { chessboard(r1, c1 + half_size, r2, c2, half_size); } else // 不在此棋盘,将此棋盘左下角设为相应的骨牌号 { board[r1 + half_size - 1][c1 + half_size] = d; chessboard(r1, c1 + half_size, r1 + half_size - 1, c1 + half_size, half_size); } if(r2 >= r1 + half_size && c2 < c1 + half_size) //特殊方格在左下角子棋盘 { chessboard(r1 + half_size, c1, r2, c2, half_size); } else // 不在此棋盘,将此棋盘右上角设为相应的骨牌号 { board[r1 + half_size][c1 + half_size - 1] = d; chessboard(r1 + half_size, c1, r1 + half_size, c1 + half_size - 1, half_size); } if(r2 >= r1 + half_size && c2 >= c1 + half_size) //特殊方格在左上角子棋盘 { chessboard(r1 + half_size, c1 + half_size, r2, c2, half_size); } else // 不在此棋盘,将此棋盘左上角设为相应的骨牌号 { board[r1 + half_size][c1 + half_size] = d; chessboard(r1 + half_size, c1 + half_size, r1 + half_size, c1 + half_size, half_size); } } int main() { int i, j; board[2][2] = 0; chessboard(0, 0, 2, 2, BOARD_SIZE); for(i = 0; i < BOARD_SIZE; i++) { for(j = 0; j < BOARD_SIZE; j++) { printf("%-4d", board[i][j]); } printf("\n"); } }

#include<iostream> using namespace std; int tile=1; //L型骨牌的编号(递增) int board[100][100]; //棋盘 /***************************************************** * 递归方式实现棋盘覆盖算法 * 输入参数: * tr--当前棋盘左上角的行号 * tc--当前棋盘左上角的列号 * dr--当前特殊方格所在的行号 * dc--当前特殊方格所在的列号 * size:当前棋盘的:2^k *****************************************************/ void chessBoard ( int tr, int tc, int dr, int dc, int size ) { if ( size==1 ) //棋盘方格大小为1,说明递归到最里层 return; int t=tile++; //每次递增1 int s=size/2; //棋盘中间的行、列号(相等的) //检查特殊方块是否在左上角子棋盘中 if ( dr<tr+s && dc<tc+s ) //在 chessBoard ( tr, tc, dr, dc, s ); else //不在,将该子棋盘右下角的方块视为特殊方块 { board[tr+s-1][tc+s-1]=t; chessBoard ( tr, tc, tr+s-1, tc+s-1, s ); } //检查特殊方块是否在右上角子棋盘中 if ( dr<tr+s && dc>=tc+s ) //在 chessBoard ( tr, tc+s, dr, dc, s ); else //不在,将该子棋盘左下角的方块视为特殊方块 { board[tr+s-1][tc+s]=t; chessBoard ( tr, tc+s, tr+s-1, tc+s, s ); } //检查特殊方块是否在左下角子棋盘中 if ( dr>=tr+s && dc<tc+s ) //在 chessBoard ( tr+s, tc, dr, dc, s ); else //不在,将该子棋盘右上角的方块视为特殊方块 { board[tr+s][tc+s-1]=t; chessBoard ( tr+s, tc, tr+s, tc+s-1, s ); } //检查特殊方块是否在右下角子棋盘中 if ( dr>=tr+s && dc>=tc+s ) //在 chessBoard ( tr+s, tc+s, dr, dc, s ); else //不在,将该子棋盘左上角的方块视为特殊方块 { board[tr+s][tc+s]=t; chessBoard ( tr+s, tc+s, tr+s, tc+s, s ); } } void main() { int size; cout<<"输入棋盘的size(大小必须是2的n次幂): "; cin>>size; int index_x,index_y; cout<<"输入特殊方格位置的坐标: "; cin>>index_x>>index_y; chessBoard ( 0,0,index_x,index_y,size ); for ( int i=0; i<size; i++ ) { for ( int j=0; j<size; j++ ) cout<<board[i][j]<<"/t"; cout<<endl; } }

#include<iostream> #include<vector> #include<stack> using namespace std; vector<vector<int> > board(4);//棋盘数组,也可以作为参数传递进chessBoard中去,作为全局变量可以减少参数传递 stack<int> stI; //记录当前所使用的骨牌号码,使用栈顶元素填充棋盘数组 int sL = 0; //L型骨牌序号 //所有下标皆为0开始的C C++下标 void chessBoard(int uRow, int lCol, int specPosR, int specPosC, int rowSize) { if(rowSize ==1) return; //static int sL = 0;棋牌和骨牌都可以用static代替,如果不喜欢用全局变量的话。 sL++; stI.push(sL); //每递归深入一层,就把一个骨牌序号入栈 int halfSize = rowSize/2;//拆分 //注意:下面四个if else,肯定是只有一个if成立,然后执行if句,而肯定有三个else语句要执行的,因为肯定有一个是特殊位置,而其他三个是空白位置,需要填充骨牌。 //1如果特殊位置在左上角区域,则继续递归,直到剩下一个格子,并且该格子已经填充,遇到函数头一句if(rowSize == 1) return;就跳出一层递归。 //注意是一个区域或子棋盘,有一个或者多个格子,并不是就指一个格子。 if(specPosR<uRow+halfSize && specPosC<lCol+halfSize) chessBoard(uRow, lCol, specPosR, specPosC, halfSize); //如果其他情况 else { board[uRow+halfSize-1][lCol+halfSize-1] = stI.top(); //因为特殊位置不在,所以可以选择任意一个空格填充,但是本算法只填充左上角(也许不止一个格,也许有很多个格子)区域的右下角。大家仔细查一下,就知道下标[uRow+halfSize-1][lCol+halfSize-1]是本区域中最右下角的一个格子的下标号。 chessBoard(uRow, lCol, uRow+halfSize-1, lCol+halfSize-1, halfSize); //然后是递归填充这个区域的其他空白格子。因为上一句已经填充了[uRow+halfSize-1][lCol+halfSize-1]这个格子,所以,这个下标作为特殊位置参数传递进chessBoard中。 } //2右上角区域,解析类上 if(specPosR<uRow+halfSize && specPosC>=lCol+halfSize) chessBoard(uRow, lCol+halfSize, specPosR, specPosC, halfSize); else { board[uRow+halfSize-1][lCol+halfSize] = stI.top(); chessBoard(uRow, lCol+halfSize, uRow+halfSize-1, lCol+halfSize, halfSize); } //3左下角区域,类上 if(specPosR>=uRow+halfSize && specPosC<lCol+halfSize) chessBoard(uRow+halfSize, lCol, specPosR, specPosC, halfSize); else { board[uRow+halfSize][lCol+halfSize-1] = stI.top(); chessBoard(uRow+halfSize, lCol, uRow+halfSize, lCol+halfSize-1, halfSize); } //4右下角区域,类上 if(specPosR>=uRow+halfSize && specPosC>=lCol+halfSize) chessBoard(uRow+halfSize, lCol+halfSize, specPosR, specPosC, halfSize); else { board[uRow+halfSize][lCol+halfSize] = stI.top(); chessBoard(uRow+halfSize, lCol+halfSize, uRow+halfSize, lCol+halfSize, halfSize); } stI.pop();//本次骨牌号填充了三个格,填充完就出栈 } void test() { //初始化数组 for(int i=0; i<4; i++) { board[i].resize(4); } chessBoard(0, 0, 3, 3, 4); //特殊位置填充0 board[3][3] = 0; //序列输出 for(int j=0; j<4; j++) { for(int i=0; i<4; i++) cout<<board[j][i]<<"\t"; cout<<endl; } cout<<endl; } int main() { test(); return 0; }
五、(三)分治法之快速排序
举例:


代码实现
/** 快速排序算法 */ void sort(int a[6], int left, int right) { //如果左边索引大于或者等于右边的索引就代表已经整理完成一个组了 if(left >= right) { return ; } int i = left; int j = right; int key = a[left]; /*控制在当组内寻找一遍*/ while(i < j) { while(i < j && key <= a[j]) /*而寻找结束的条件就是,1,找到一个小于或者大于key的数(大于或小于取决于你想升 序还是降序)2,没有符合条件1的,并且i与j的大小没有反转*/ { //向前寻找 j--; } a[i] = a[j]; /*找到一个这样的数后就把它赋给前面的被拿走的i的值(如果第一次循环且key是 a[left],那么就是给key)*/ while(i < j && key >= a[i]) /*这是i在当组内向前寻找,同上,不过注意与key的大小关系停止循环和上面相反, 因为排序思想是把数往两边扔,所以左右两边的数大小与key的关系相反*/ { i++; } a[j] = a[i]; } /*当在当组内找完一遍以后就把中间数key回归*/ a[i] = key; /*最后用同样的方式对分出来的左边的小组进行同上的做法*/ sort(a, left, i - 1); /*用同样的方式对分出来的右边的小组进行同上的做法*/ sort(a, i + 1, right); /*当然最后可能会出现很多分左右,直到每一组的i = j 为止*/ } int main(int argc, const char * argv[]) { int a[6] = {1, 10, 8, 7, 4, 3}; sort(a, 0, 5); for (int i = 0; i < 6; i ++) { printf("i = %d\n",a[i]); } }
标签:完全 gem printf ddl orm quic 区域 解析 函数
原文地址:https://www.cnblogs.com/1138720556Gary/p/11073808.html