标签：实现   tail   最小   维护   优化   大致   inf   vat   大于   

1.基本算法

快速排序是一种分治的排序算法。它将一个数组分成两个子数组，再对这两个数组独立地排序。快速排序的大致过程如下图所示:

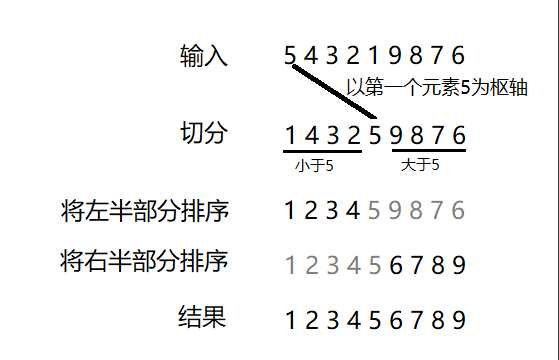
整个算法分为三步:

1. 选择一个元素作为枢轴(pivot)
2. 扫描并交换数组元素，使得小于枢轴的元素处于左边，大于枢轴的元素处于右边，这个过程称为切分(partition)
3. 对枢轴左边部分和右边部分的元素递归调用快速排序算法

1.1 快速排序的代码实现

    public static void sort(Comparable[] a) {
        sort(a, 0, a.length - 1);
    }

    private static void sort(Comparable[] a, int low, int high) {
        if (high <= low) return;
        // 切分（请见“快速排序的切分”）
        int j = partition(a, low, high);  
        // 将左半部分a[low .. j-1]排序
        sort(a, low, j - 1);
        // 将右半部分a[j+1 .. high]排序
        sort(a, j + 1, high);
    }

1.2 切分实现

1.2.1 从两边向中间扫描

• 选择第一个元素作为枢轴
• 循环：指针i向右扫描，指针j向左扫描
• 指针i从第二个元素开始向右扫描找到比枢轴大的元素；
• 指针j从最后一个元素开始向左扫描找到比枢轴小的元素；
• 交换i和j的元素使得a[low..i]<=a[j..high]
• 交换枢轴与与指针j的元素,因为指针j的元素在退出循环后必然小于等于枢轴
• 达成a[low..j-1] <= a[j] <= a[j+1..high]

代码实现如下:

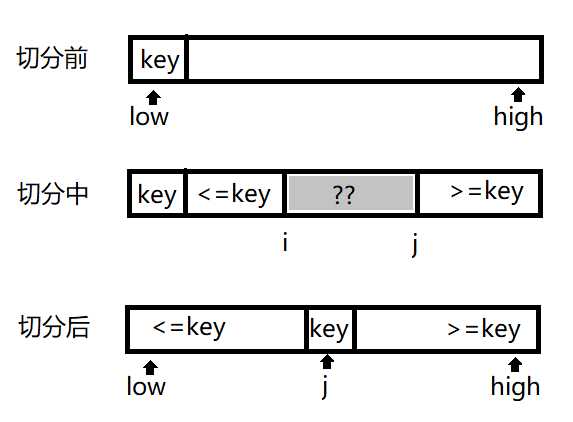
// 将数组切分为a[low..i-1], a[i], a[i+1..high]
    static int partition(Comparable[] a, int low, int high) {
        // 指针i向右扫描，指针j向左扫描
        int i = low, j = high + 1;
        // 切分元素
        Comparable key = a[low];
        while (true) {
            // 扫描左右，检查扫描是否结束并交换元素
            while (less(a[++i], key)) if (i == high) break;
            while (less(key, a[--j])) if (j == low) break;
            if (i >= j) break;
            swap(a, i, j);
        }
        // 将key = a[j]放入正确的位置
        swap(a, low, j);
        // a[low..j-1] <= a[j] <= a[j+1..high] 达成
        return j;
    }

1.2.2 从左向右扫描

• 选择第一个元素作为枢轴
• 循环：指针i和j同时从第二个元素开始向右扫描
  • 指针j向右扫描找到小于枢轴的元素
  • 交换指针i和j的元素
  • 指针i向右移动，指针i左边的元素均小于等于枢轴，即a[low..i-1]<=key
• 交换枢轴与与指针i的元素,因为指针i的元素在退出循环后必然小于等于枢轴
• 达成a[low..i-1] <= a[i] <= a[i+1..high]

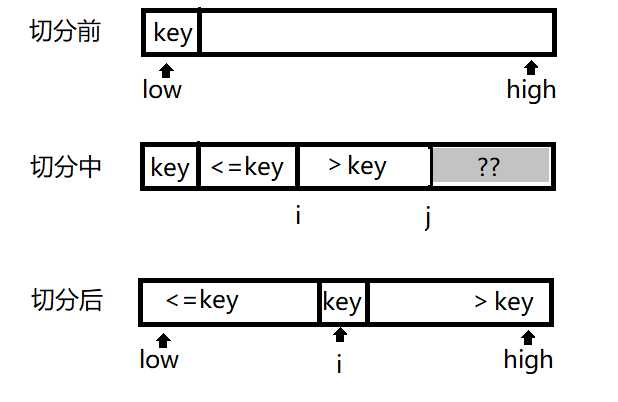
代码实现如下:

    // 将数组切分为a[low..i-1], a[i], a[i+1..high]
    static int partition2(Comparable[] a, int low, int high) {
        // 两个指针均向右扫描
        int i = low+1;
        // 切分元素
        Comparable key = a[low];
        for (int j = i + 1; j <= high; j++) {
            //指针j向右扫描找到小于枢轴的元素
            if (less(a[j], key)) {
                //交换指针i和j的元素，确保指针i左边的元素小于等于枢轴
                swap(a,i,j);
                //指针i只有交换元素时才移动
                i=i+1;
            }
        }
        // 将key = a[i]放入正确的位置
        swap(a, low, i);
        // a[low..i-1] <= a[i] <= a[i+1..high] 达成
        return i;
    }

1.3 单链表排序

单链表的快排思路与数组的快排一致，但是由于单链表的指针移动只能单向移动，因此只能选择从左向右扫描的切分方法。

1.3.1 链表的快排

• 引入尾节点用于结束条件判断，作用类似于数组的长度n
• 切分为两部分并返回枢轴的位置
• 对于枢轴左边和枢轴右边的链表递归调用快速排序

    static class Node {
        int val;
        Node next;
    }
    void quickSortList(Node head){
        quickSortList(head,null);
    }
    void quickSortList(Node head,Node tail){
        if(head==null||head==tail){
            return;
        }
        Node pivot = partitionList(head, tail);
        quickSortList(head,pivot);
        quickSortList(pivot.next,tail);
    }

1.3.2 链表的切分

与1.2.2的从左向右扫描思路一致

    static Node partitionList(Node head, Node tail) {
        if (head == null || head.next == null) {
            return head;
        }
        int key = head.val;
        Node i = head.next;
        for (Node j = i.next; j != tail; j = j.next) {
            if (j.val < key) {
                swap(i, j);
                i = i.next;
            }
        }
        swap(head, i);
        return i;
    }

    static void swap(Node i, Node j) {
        int temp = i.val;
        i.val = j.val;
        j.val = temp;
    }

2. 提高性能

2.1 切换到插入排序

• 对于小数组，快速排序比插入排序慢
• 因为递归，快速排序的sort()方法在小数组中也会调用自己

因此在排序小数组时应该切到插入排序。将1.1的sort实现中的语句:

if (high <= low) return;

替换成:

if (high <= low+M) {Insertion.sort(a, low, high); return;}

M为一个常数，最佳数值与系统相关，一般选择5~15都可以得到令人满意的结果。

2.2 精选枢轴

枢轴的选取非常关键，如果每次切分时，枢轴都选用了最小的那个元素，快速排序就退化为冒泡排序了。解决办法是使用数组的一小部分元素的中位数作为枢轴来切分数组，但是代价是需要计算中位数。人们发现取样3个数并选择中位数作为枢轴，效果最好。

2.3 处理相同元素

一个元素全部相同的子数组是不需要排序的，但是基础的快速排序算法还是会将它切分为更小的数组并递归调用排序。

一个简单的办法是将数组切分为三部分，分别对应小于、等于和大于枢轴的数组元素

2.3.1 三向切分

从左到右遍历数组一次，维护一个指针lt使得a[low..lt]中的元素都小于key，一个指针gt使得a[gt+1..high]中的元素都大于key，一个指针i使得a[lt..i]中的元素都等于key，a[i..gt]中的元素还未确定，如下图所示:

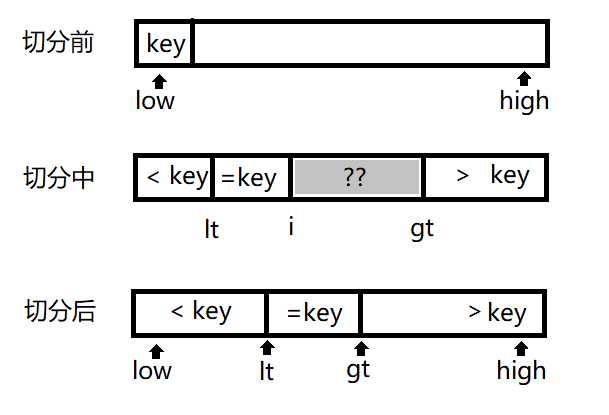
代码实现如下:

public class Quick3Way {
    private static void sort(Comparable[] a, int lo, int hi) {
        //调用此方法的公有方法sort() 请见算法2 .5 if (hi <= lo) return;
        int lt = lo, i = lo + 1, gt = hi;
        Comparable v = a[lo];
        while (i <= gt) {
            int cmp = a[i].compareTo(v);
            if (cmp < 0) swap(a, lt++, i++);
            else if (cmp > 0) swap(a, i, gt--);
            else i++;
        }
        //现在 a[ lo..lt - 1] <v = a[lt..gt] <a[gt + 1..hi] 成立
        sort(a, lo, lt - 1);
        sort(a, gt + 1, hi);
    }

    private static void swap(Comparable[] a, int i, int j) {
        Comparable temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

2.4 JDK的快速排序优化

Arrays.sort()的排序只有在数组小于286才使用快速排序，更大的数组则使用更稳定的自底向上的归并排序。

快速排序使用了上述三种优化方法。

2.4.1 小数组插入排序

2.4.2 计算中位数

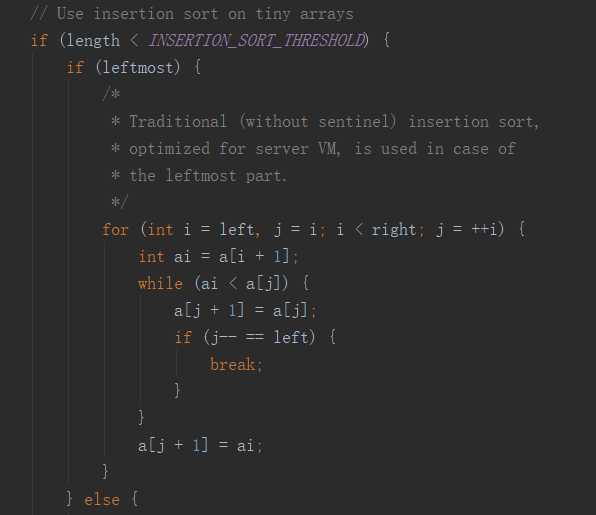
使用五值取中法找到中位数：

2.4.3 三向切分

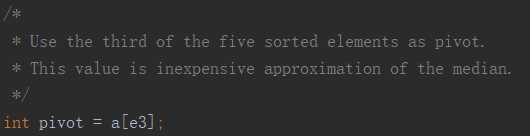
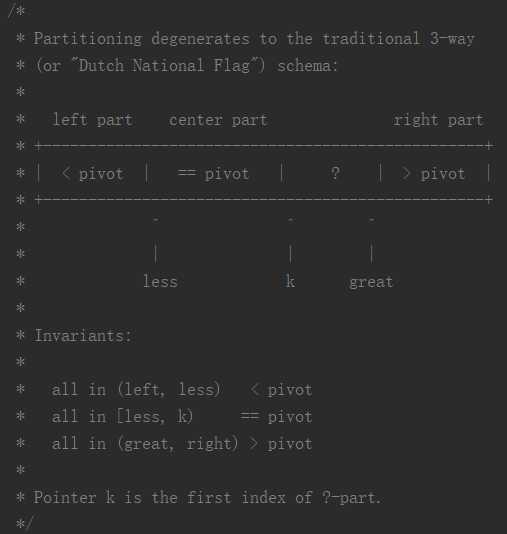
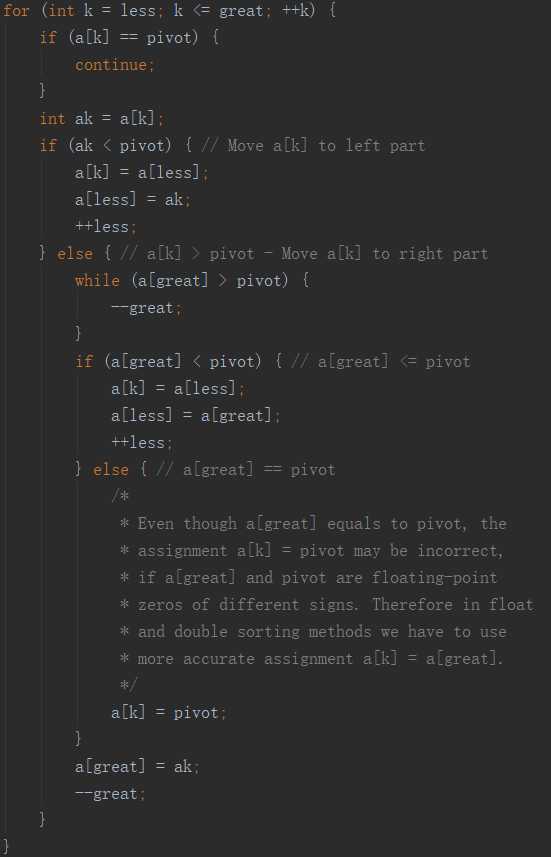
这是三向切分可读性更差的版本，原理与2.3.1相同：

快速排序从入门到精通

标签：实现   tail   最小   维护   优化   大致   inf   vat   大于   

原文地址：https://www.cnblogs.com/datartvinci/p/11109471.html