42.接雨水 Trapping Rain Water

标签：void   null   集合   中间   solution   tar   技术   else   i++   

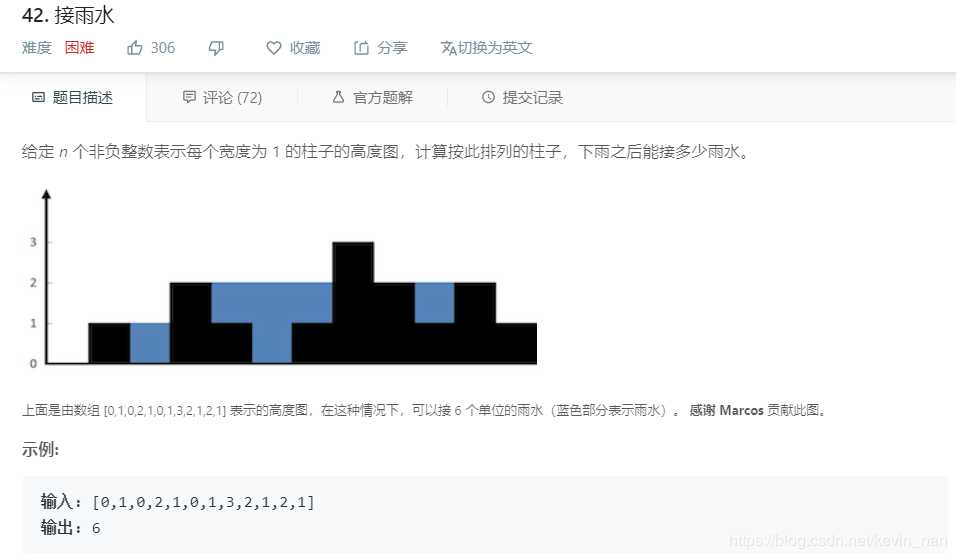
本人的解法：

public class Main {
    public int trap(int[] height) {
        // 统计雨水总数//temp登记最大值
        int sum = 0;
        if (height.length != 0) 
        {
            int temp = height[0];
            int temp2 = 0;
            int temp3 = height[0];
            int temp4 = height[height.length - 1];          
            //跟踪最大值的位置
            for (int x = 0; x < height.length; x++) 
            {
                if (height[x] > temp) {
                    temp = height[x];
                    temp2 = x;
                }
            }   
            // 进行累加 这里采用两头向中间逐级判断
            //第一个for
            for (int i = 1; i <= temp2; i++) 
            {
 
                if (height[i] > temp3) 
                {
                    temp3 = height[i];
                } 
                else 
                {
                    sum = sum + temp3 - height[i];
                }
            }
            //第二个for
            for (int i = height.length - 1; i >= temp2; i--) 
            {
                if (height[i] > temp4) 
                {
                    temp4 = height[i];
                } 
                else 
                {
                    sum = sum + temp4 - height[i];
                }
            }
            return sum;
        } 
            //空集合
        else 
        {
            return 0;
        }
    }
    //测试代码
    public static void main(String[] args) {
        Main m = new Main();
        int[] arr = { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1 };
        System.out.println(m.trap(arr));
    }
}
//////////////////////////////简化版
public class Solution {
    public int trap(int[] A) {
        int left = 0 , right = A.length-1;
        int sum = 0;
        int pre = 0;
        while(left < right){
            sum += (Math.min(A[left], A[right])-pre) * (right-left-1);
            pre = Math.min(A[left],A[right]);
            if(A[left] > A[right]){ 
                int temp = right-1;
                while(left < temp && A[temp] <= pre){sum-=A[temp];temp--;}
                if(left < temp) sum -= pre;
                right = temp;
            }else{
                int temp = left+1;
                while(temp < right && A[temp] <= pre){sum-=A[temp];temp++;}
                if(temp < right) sum -= pre;
                left = temp;
            }
        }
        return sum;
    }
}
?

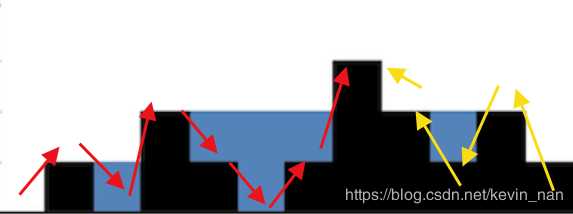
最大值的位置只选一个（如果几个最大值一样的话 也只选其中一个）
其他解法：
1、填充集合为凸集 填充的单位

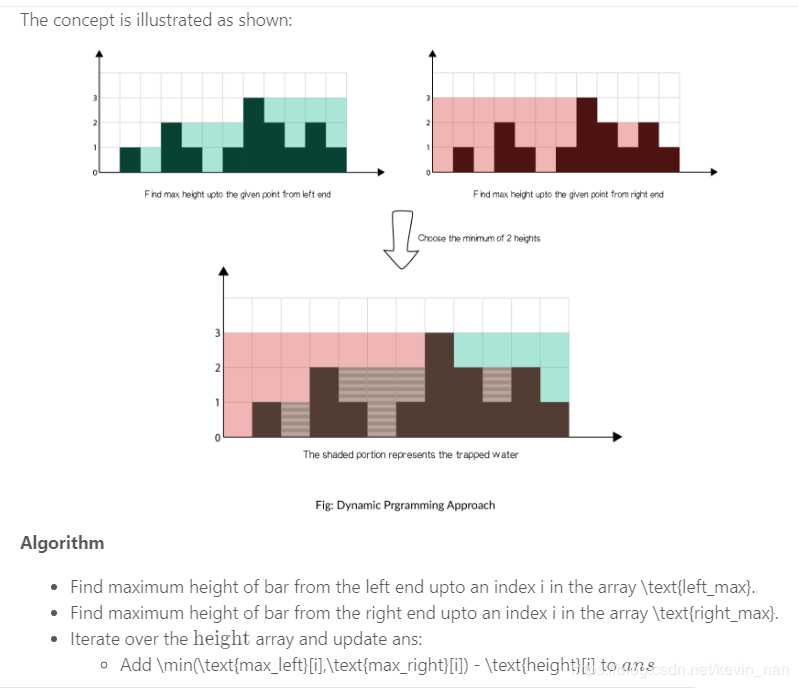
2、

class Solution {
    public int trap(int[] height) {
        if(height.length<3){
            return 0;
        }
        return find(height,0,height.length-1);
    }
    public int find(int[] height,int start,int end){
        if(end-start<2){//递归的终点
            return 0;
        }
        int max=-1,tmp=-1,min_two=Math.min(height[start],height[end]),sum=0;;
        for(int i=start+1;i<end;i++){
            //这一句写在哪里都行
            sum=sum+(min_two-height[i]);
            if(height[i]>max){
                max=height[i];
                tmp=i;
            }
        }  
        if(max<min_two){//上面的加法其实应该在这里，转移到上面和在这里其实都一样
            //sum=sum+(min_two-height[i]);
            return sum;
        }else{//其实这里还可以优化一下当中间的max值等于start或者end的时候，当它等于start,那么直接计算即可，不用进行下一次递归，因为下一次递归会再扫描一遍
            return find(height,start,tmp)+find(height,tmp,end);
        }
    }
}

public int trap(int[] A) {
        if (A==null) return 0;
        Stack<Integer> s = new Stack<Integer>();
        int i = 0, maxWater = 0, maxBotWater = 0;
        while (i < A.length){
            if (s.isEmpty() || A[i]<=A[s.peek()]){
                s.push(i++);
            }
            else {
                int bot = s.pop();
                maxBotWater = s.isEmpty()? // empty means no il
                0:(Math.min(A[s.peek()],A[i])-A[bot])*(i-s.peek()-1);
                maxWater += maxBotWater;
            }
        }
        return maxWater;
    }

42.接雨水 Trapping Rain Water

标签：void   null   集合   中间   solution   tar   技术   else   i++   

原文地址：https://www.cnblogs.com/cznczai/p/11149678.html