标签:递归 n的阶乘 code image logs strong 递增 href 自己

汉诺塔:

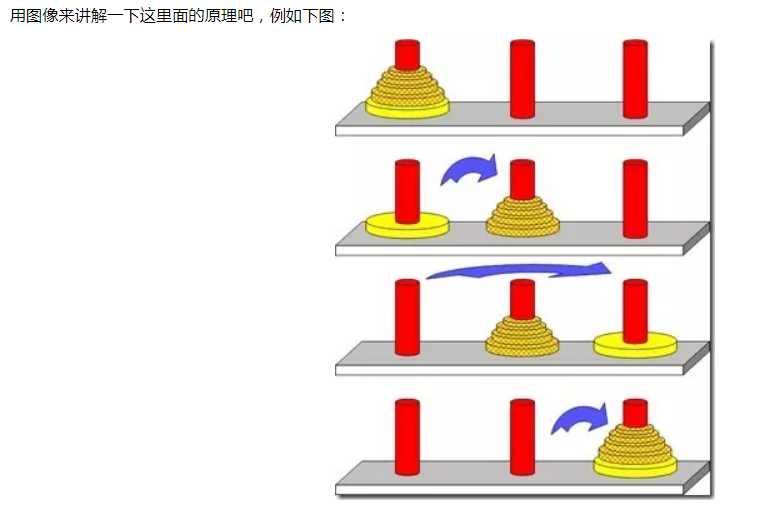
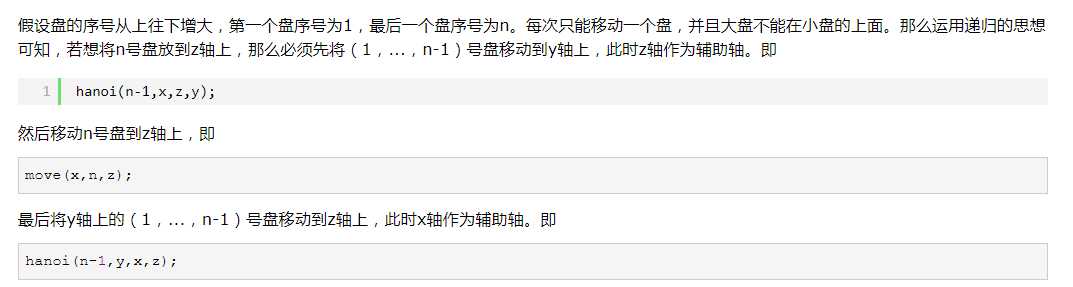
什么时候要用到递归算法:
1.解决问题时,可以把一个问题转化为一个新的问题,而这个新的问题的解决方法仍与原问题的解法相同,只是所处理的对象有所不同,这些被处理的对象之间是有规律的递增或递减;
2.可以通过转化过程是问题得到解决;
3.必定要有一个明确的结束递归的条件,否则递归将会无止境地进行下去,直到耗尽系统资源。也就是说必须要某个终止递归的条件。如求阶乘问题,我们要求n的阶乘(n!),可以把这个问题转化为n*(n-1)!,而要求(n-1)!又可转化为(n-1)*(n-2)!,……,这里面都有一个一个数乘以另一个数阶乘的问题,被处理的对象分别是n,n-1,……,是有规律的递减。但是我们不能让程序无休止的乘下去,必须要给他一个结束条件,该问题恰好有一个结束条件,那就是当n=0时,0!=1。
标签:递归 n的阶乘 code image logs strong 递增 href 自己
原文地址:https://www.cnblogs.com/wzdnwyyu/p/11168971.html