标签:sam 法线 res mit poj 均方误差 根据 back follow
1、线性回归
假设线性函数如下:
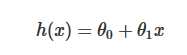
假设我们有10个样本x1,y1),(x2,y2).....(x10,y10),求解目标就是根据多个样本求解theta0和theta1的最优值。
什么样的θ最好的呢?最能反映这些样本数据之间的规律呢?
为了解决这个问题,我们需要引入误差分析预测值与真实值之间的误差为最小。
2、梯度下降算法
梯度下降的场景:
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。 但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。 具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。 然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
梯度下降实现:原理baidu,这里略过。下图来自internet,解释的非常到位。
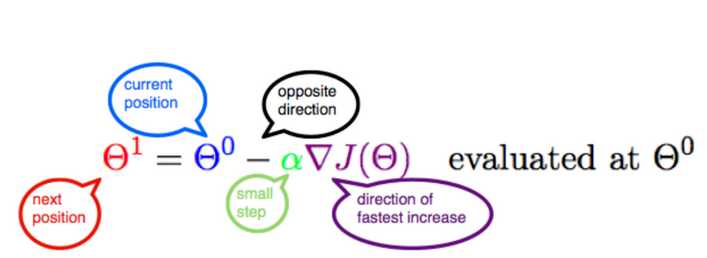
α含义 α在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,以保证不要步子跨的太大,就是不要走太快,错过了最低点。
同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。所以α的选择在梯度下降法中往往是很重要的!α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点! 梯度要乘以一个负号 梯度前加一个负号,就意味着朝着梯度相反的方向前进!梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号。
实现梯度下降,需要定义一个代价函数,比如:
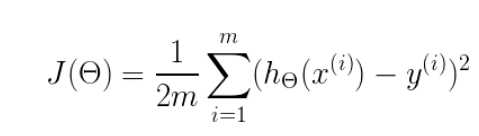
这是均方误差代价函数
m是数据集中点的个数 二分之一(½)是一个常量,这样是为了在求梯度的时候,二次方乘下来就和这里的½抵消了,自然就没有多余的常数系数,方便后续的计算,同时对结果不会有影响 y 是数据集中每个点的真实y坐标的值 h 是预测函数,根据每一个输入x,根据Θ 计算得到预测的y值
即: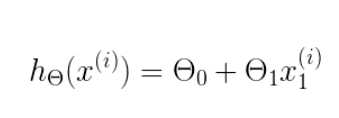
3、最终求解公式,代价函数是j=h(x)-y
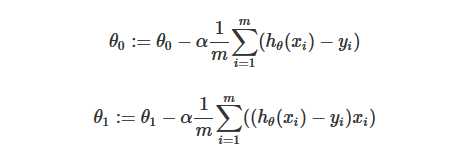
/** * @Author: xu.dm * @Date: 2019/7/16 21:52 * @Description: 批量梯度下降算法解决线性回归 y = theta0 + theta1*x 的参数求解。 * 本例实现一元数据求解二元参数。 * BGD(批量梯度下降)算法的线性回归是一种迭代聚类算法,其工作原理如下: * BGD给出了数据集和目标集,试图找出适合目标集的数据集的最佳参数。 * 在每次迭代中,算法计算代价函数(cost function)的梯度并使用它来更新所有参数。 * 算法在固定次数的迭代后终止(如本实现中所示)通过足够的迭代,算法可以最小化成本函数并找到最佳参数。 * Linear Regression with BGD(batch gradient descent) algorithm is an iterative clustering algorithm and works as follows: * Giving a data set and target set, the BGD try to find out the best parameters for the data set to fit the target set. * In each iteration, the algorithm computes the gradient of the cost function and use it to update all the parameters. * The algorithm terminates after a fixed number of iterations (as in this implementation) * With enough iteration, the algorithm can minimize the cost function and find the best parameters * * This implementation works on one-dimensional data. And find the two-dimensional theta. * It find the best Theta parameter to fit the target. * * <p>Input files are plain text files and must be formatted as follows: * <ul> * <li>Data points are represented as two double values separated by a blank character. The first one represent the X(the training data) and the second represent the Y(target). * Data points are separated by newline characters.<br> * For example <code>"-0.02 -0.04\n5.3 10.6\n"</code> gives two data points (x=-0.02, y=-0.04) and (x=5.3, y=10.6). * </ul> */ public class LinearRegression { public static void main(String args[]) throws Exception{ final ParameterTool params = ParameterTool.fromArgs(args); final ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment(); env.getConfig().setGlobalJobParameters(params); final int iterations = params.getInt("iterations", 10); // get input x data from elements DataSet<Data> data; if (params.has("input")) { // read data from CSV file data = env.readCsvFile(params.get("input")) .fieldDelimiter(" ") .includeFields(true, true) .pojoType(Data.class); } else { System.out.println("Executing LinearRegression example with default input data set."); System.out.println("Use --input to specify file input."); data = LinearRegressionData.getDefaultDataDataSet(env); } // get the parameters from elements DataSet<Params> parameters = LinearRegressionData.getDefaultParamsDataSet(env); // set number of bulk iterations for SGD linear Regression IterativeDataSet<Params> loop = parameters.iterate(iterations); DataSet<Params> newParameters = data // compute a single step using every sample .map(new SubUpdate()).withBroadcastSet(loop,"parameters") // sum up all the steps .reduce(new UpdateAccumulator()) // average the steps and update all parameters .map(new Update()); // feed new parameters back into next iteration DataSet<Params> result = loop.closeWith(newParameters); // emit result if (params.has("output")) { result.writeAsText(params.get("output")); // execute program env.execute("Linear Regression example"); } else { System.out.println("Printing result to stdout. Use --output to specify output path."); result.print(); } } /** * A simple data sample, x means the input, and y means the target. */ public static class Data implements Serializable{ public double x, y; public Data() {} public Data(double x, double y) { this.x = x; this.y = y; } @Override public String toString() { return "(" + x + "|" + y + ")"; } } /** * A set of parameters -- theta0, theta1. */ public static class Params implements Serializable { private double theta0, theta1; public Params() {} public Params(double x0, double x1) { this.theta0 = x0; this.theta1 = x1; } @Override public String toString() { return theta0 + " " + theta1; } public double getTheta0() { return theta0; } public double getTheta1() { return theta1; } public void setTheta0(double theta0) { this.theta0 = theta0; } public void setTheta1(double theta1) { this.theta1 = theta1; } public Params div(Integer a) { this.theta0 = theta0 / a; this.theta1 = theta1 / a; return this; } } /** * Compute a single BGD type update for every parameters. * h(x) = theta0*X0 + theta1*X1,假设X0=1,则h(x) = theta0 + theta1*X1,即y = theta0 + theta1*x * 代价函数:j=h(x)-y,这里用的是比较简单的cost function * theta0 = theta0 - α∑(h(x)-y) * theta1 = theta1 - α∑((h(x)-y)*x) * */ public static class SubUpdate extends RichMapFunction<Data, Tuple2<Params, Integer>> { private Collection<Params> parameters; private Params parameter; private int count = 1; /** Reads the parameters from a broadcast variable into a collection. */ @Override public void open(Configuration parameters) throws Exception { this.parameters = getRuntimeContext().getBroadcastVariable("parameters"); } @Override public Tuple2<Params, Integer> map(Data in) throws Exception { for (Params p : parameters){ this.parameter = p; } //核心计算,对于y = theta0 + theta1*x 假定theta0乘以X0=1,所以theta0计算不用乘以in.x double theta0 = parameter.theta0 - 0.01 * ((parameter.theta0 + (parameter.theta1 * in.x)) - in.y); double theta1 = parameter.theta1 - 0.01 * (((parameter.theta0 + (parameter.theta1 * in.x)) - in.y) * in.x); System.out.println("theta0: "+theta0+" , theta1: "+theta1); return new Tuple2<>(new Params(theta0, theta1), count); } } /** * Accumulator all the update. * */ public static class UpdateAccumulator implements ReduceFunction<Tuple2<Params, Integer>> { @Override public Tuple2<Params, Integer> reduce(Tuple2<Params, Integer> val1, Tuple2<Params, Integer> val2) { double newTheta0 = val1.f0.theta0 + val2.f0.theta0; double newTheta1 = val1.f0.theta1 + val2.f0.theta1; Params result = new Params(newTheta0, newTheta1); return new Tuple2<>(result, val1.f1 + val2.f1); } } /** * Compute the final update by average them. */ public static class Update implements MapFunction<Tuple2<Params, Integer>, Params> { @Override public Params map(Tuple2<Params, Integer> arg0) throws Exception { return arg0.f0.div(arg0.f1); } } }
数据准备:
public class LinearRegressionData { // We have the data as object arrays so that we can also generate Scala Data // Sources from it. public static final Object[][] PARAMS = new Object[][] { new Object[] { 0.0, 0.0 } }; public static final Object[][] DATA = new Object[][] { new Object[] { 0.5, 1.0 }, new Object[] { 1.0, 2.0 }, new Object[] { 2.0, 4.0 }, new Object[] { 3.0, 6.0 }, new Object[] { 4.0, 8.0 }, new Object[] { 5.0, 10.0 }, new Object[] { 6.0, 12.0 }, new Object[] { 7.0, 14.0 }, new Object[] { 8.0, 16.0 }, new Object[] { 9.0, 18.0 }, new Object[] { 10.0, 20.0 }, new Object[] { -0.08, -0.16 }, new Object[] { 0.13, 0.26 }, new Object[] { -1.17, -2.35 }, new Object[] { 1.72, 3.45 }, new Object[] { 1.70, 3.41 }, new Object[] { 1.20, 2.41 }, new Object[] { -0.59, -1.18 }, new Object[] { 0.28, 0.57 }, new Object[] { 1.65, 3.30 }, new Object[] { -0.55, -1.08 } }; public static DataSet<LinearRegression.Params> getDefaultParamsDataSet(ExecutionEnvironment env) { List<LinearRegression.Params> paramsList = new LinkedList<>(); for (Object[] params : PARAMS) { paramsList.add(new LinearRegression.Params((Double) params[0], (Double) params[1])); } return env.fromCollection(paramsList); } public static DataSet<LinearRegression.Data> getDefaultDataDataSet(ExecutionEnvironment env) { List<LinearRegression.Data> dataList = new LinkedList<>(); for (Object[] data : DATA) { dataList.add(new LinearRegression.Data((Double) data[0], (Double) data[1])); } return env.fromCollection(dataList); } }
flink 批量梯度下降算法线性回归参数求解(Linear Regression with BGD(batch gradient descent) )
标签:sam 法线 res mit poj 均方误差 根据 back follow
原文地址:https://www.cnblogs.com/asker009/p/11202480.html