标签:ret i+1 UNC append 初始 size com 一个人 i++
问题:有100张写着数字1~100的牌,并按顺序排列。最开始所有牌都是背面朝上放置。某人从第2张牌开始,隔1张牌翻牌。然后第2, 4, 6, …,100张牌就会变成正面朝上。接下来,另一个人从第3张牌开始,隔2张牌翻牌(原本背面朝上的,翻转成正面朝上;原本正面朝上的,翻转成背面朝上)。再接下来,又有一个人从第4张牌开始,隔3张牌翻牌。像这样,从第n张牌开始,每隔n-1张牌翻牌,直到没有可翻动的牌为止。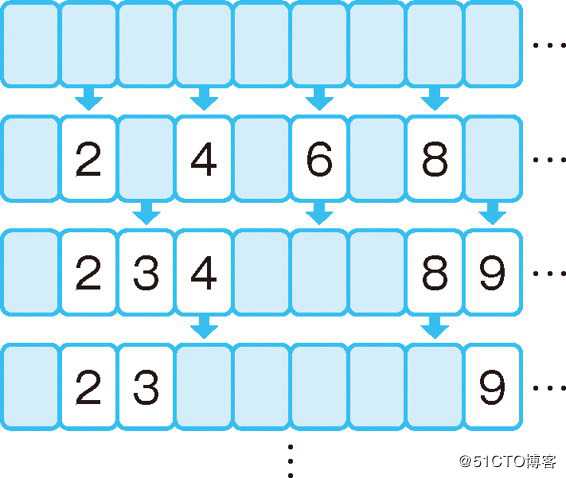
求当所有牌不再变动时,所有背面朝上的牌的数字。
这道题思路有很多种:
思路1
设i为轮次,从1开始,到99结束。设j为牌的下标。
每一轮都按题意找到对应下标的牌逐个进行翻转。
思路2
设i为轮次,从1开始,到99结束;设j为牌的下标。
每一轮都对符合要求的所有牌进行翻转。
思路3
牌只有在偶数次翻转时才会背面朝上。
而牌翻转的时机是:步长为该牌面的约数时,这一点不太好理解,举例说明。
如:4号牌,初始是背面朝上,
第1轮,从2号牌开始,步长为2,4号牌被翻动,正面朝上;
第2轮,从3号牌开始,步长为3,4号牌不被翻动;
第3轮,从4号牌开始,步长为4,4号牌被翻动,背面朝上;
以后不会再被翻动
可以看到,当步长为2,4时,4号牌都会发生翻动,而2,4都是4的约数。
如:6号牌,初始是背面朝上,
第1轮,从2号牌开始,步长为2,6号牌被翻动,正面朝上;
第2轮,从3号牌开始,步长为3,6号牌被翻动,背面朝上;
第3轮,从4号牌开始,步长为4,6号牌不被翻动;
第4轮,从5号牌开始,步长为5,6号牌不被翻动;
第5轮,从6号牌开始,步长为6,6号牌被翻动,正面朝上;
以后不会再被翻动
可以看到,当步长为2,3,6时,6号牌都会发生翻动,而2,3,6都是6的约数。
如果算上1这个所有自然数的约数,那只要约数的个数是奇数个,最终都会背面朝上。
还可以继续归纳:
比如:
12号牌,约数为1,2,3,4,6,12,共有6个约数,最终是正面朝上;
16号牌,约数为1,2,4,8,16,共用有5个约数,最终是背面朝上;
25号牌,约数为1,5,25,共有3个约数,最终是背面朝上;
注意到,所有背面朝上的牌4,16,25,它们都是平方数。
所以这道题最终就变成了找出1-100中所有的平方数。
以下按上述三条思路分别给出PHP和Golang的代码
PHP
// 按顺序进行翻牌,i为牌下标,j为牌下标+步长
function flip1()
{
$size = 100;
$cards = array_fill(0, $size, 0); // 初始化数组
// i为轮次
for ($i = 1; $i <= $size; $i++) {
// 如果当前的牌是正面,就翻过来;反之亦然。
// 每轮步长增长为i+1,
// 例如:
// 第一轮起始下标是1,步长是2(=1+1),翻1,3,5...下标的牌
// 第二轮起始下标是2,步长是3(=2+1),翻2,5,8...下标的牌
// 以此类推
for ($j = $i; $j < $size; $j += $i + 1) {
$cards[$j] = !$cards[$j];
}
}
output($cards);
}
// i为轮次,j为牌下标
// 第1轮:2,4,6...100的牌被翻转,对应的下标为1,2,3...99,(j+1)%(1+1)==0
// 第2轮:3, 6, 9...99的牌被翻转,对应的下标为2,5,8...98,(j+1)%(2+1)==0
// 以此类推,得到公式,(j+1)%(i+1)==0时,牌都会翻转
function flip2()
{
$size = 100;
$cards = array_fill(0, $size, 0); // 初始化数组
for ($i = 1; $i < $size; $i++) {
for ($j = 1; $j < $size; $j++) {
if (($j + 1) % ($i + 1) == 0) {
$cards[$j] = !$cards[$j];
}
}
}
output($cards);
}
// 当牌i翻转为偶数次时,即为背面朝上
// 当j为i的约数时,会触发一次i的翻转
// 比如:牌4,会在约数为1,2,4时被翻转
// 但所有的牌都是从约数为2开始翻,所以排除掉约数1的情况
// 此时,4号牌只翻转了2次,符合偶数次翻转的情况,所以其最终是背面朝上
function flip3()
{
$size = 100;
$tmp = array();
// i为牌面,数字为1-100的100张牌
for ($i = 1; $i <= $size; $i++) {
$flag = false;
// j为步长
for ($j = 2; $j <= $size; $j++) {
if ($i % $j == 0) {
$flag = !$flag;
}
}
if ($flag == false) {
$tmp[] = $i;
}
}
echo implode(‘ ‘, $tmp) . "\n";
}
function output($cards)
{
foreach ($cards as $key => $val) {
if (!$val) {
echo $key + 1;
echo " ";
}
}
echo "\n";
}
flip1();
flip2();
flip3();输出
1 4 9 16 25 36 49 64 81 100
1 4 9 16 25 36 49 64 81 100
1 4 9 16 25 36 49 64 81 100Golang
package main
import "fmt"
var size = 100 // 牌数
func main() {
Flip1()
Flip2()
Flip3()
}
// 初始化数据
func initCards() []bool {
var cards []bool // 存放每张牌的状态
for i := 0; i < size; i++ {
cards = append(cards, false)
}
return cards
}
// 翻牌算法1
func Flip1() {
cards := initCards()
for i := 1; i < size; i++ {
for j := i; j < size; j += i + 1 {
cards[j] = !cards[j]
}
}
PrintCards(cards)
}
// 翻牌算法2
func Flip2() {
cards := initCards()
for i := 1; i < size; i++ {
for j := i; j < size; j++ {
if (j+1)%(i+1) == 0 {
cards[j] = !cards[j]
}
}
}
PrintCards(cards)
}
// 翻牌算法3
func Flip3() {
var cards []int
for i := 1; i <= size; i++ {
flag := false
for j := 2; j <= size; j++ {
if i%j == 0 {
flag = !flag
}
}
if flag == false {
cards = append(cards, i)
}
}
fmt.Println(cards)
}
// 输出牌面
func PrintCards(cards []bool) {
var results []int
for i := 0; i < size; i++ {
if cards[i] == false {
results = append(results, i+1)
}
}
fmt.Println(results)
}输出
[1 4 9 16 25 36 49 64 81 100]
[1 4 9 16 25 36 49 64 81 100]
[1 4 9 16 25 36 49 64 81 100]标签:ret i+1 UNC append 初始 size com 一个人 i++
原文地址:https://blog.51cto.com/ustb80/2421507