标签:部分 说明 || not 相同 多个 opened cte nbsp
问题的输入是一对整数,例如(p、q),表示p和q是相连的,这里的相连是一种等价关系,即:具有自反性,对称性和传递性。
等价关系可以将对象分为多个等价类,仅当两个对象相连时他们属于一个等价类。我们的目标是编写一个程序来过滤掉序列中无意义的整数对。比如,当程序读到了p、q时,如果已知的整数对不能说明p、q是连通的,那么就将这一对整数对写入输出中,否则就可以忽略并继续处理下一对整数。我们将这类问题称作动态连通性问题。这类问题常见于以下应用
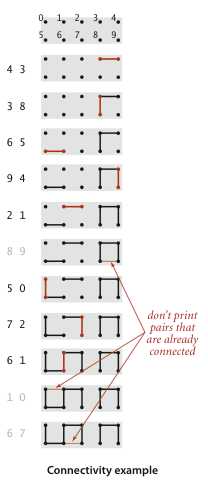
其中:(8,9)(1,0)(6,7)不输出,因为可以依靠现有的整数对说明它们是连接的。
1、网络:
其中整数代表一台计算机,整数对代表两台计算机之间的网络连接,这个程序来判定我们是否需要在p和q之间假设一条新的连接才能通信。
2、数学集合:
将输入的整数看成是不同的集合,在处理一个整数对时候我们是在判断他们是否属于同一集合,如果不是,则将p集合和q集合归并到同一集合里。
我们下面将对象称为触点,整数对称为连接,等价类称为连通分量或者简称为分量。
我们需要定义一份API:

现在对这份API做一个说明:
如果两个触点在不同的分量中,union()操作会将两个分量归并。find()分量会返回给定的触点所在的分量的标识符。connected()判断两个触点是否处在同一连通分量中。count()返回所有连通分量个数。一开始有N个连通分量。
这里我们使用以触点为索引的数组id[]来表示所有分量。将分量中某个触点的名字作为分量的标识符。初始化后我们有N个分量,每个触点都构成了只含有他自己的分量,因此将id[i]初始化为I,将find()判断它所在的分量所需要的信息保存在id[i]中,connected()方法的实现只需要一条find(p)==find(q),他返回一个Boolean值。
代码实现:

1 public class UF { 2 3 private int[] id; 4 private int count; 5 public UF(int N) 6 { 7 count=N; 8 id=new int[N]; 9 for(int i=0;i<N;i++) 10 { 11 id[i]=i; 12 } 13 } 14 15 public int count() 16 { 17 return count; 18 19 } 20 21 public boolean connected(int p,int q) 22 { 23 return find(p)==find(q); 24 } 25 public int find(int i) 26 public void union(int p,int q) 27 //这两个算法下面具体讨论 28 29 }
这种方法保证当且仅当id[p]==id[p]时,p、q是连通的,即同一连通分量里的所有触点在id[]中的值都必须相同。这意味着connected()只需要判断id[p]==id[p],当调用union()时我们首先需要判断他们是否属于同一连通分量,如果是,则不采取行动,否则就将两个分量合并,将两个集合中所有触点对应的id[]变为同一个值。我们需要遍历整个数组,将与id[p]相等的元素的值改为id[q]的值,或者将与id[q]相等的元素的值改为id[p]的值。
代码实现:

1 public class QuickFind { 2 private int[] id; 3 private int count; 4 5 6 public QuickFind(int n) { 7 count = n; 8 id = new int[n]; 9 for (int i = 0; i < n; i++) 10 id[i] = i; 11 } 12 13 public int count() { 14 return count; 15 } 16 17 18 public int find(int p) { 19 validate(p); 20 return id[p]; 21 } 22 23 24 private void validate(int p) { 25 int n = id.length; 26 if (p < 0 || p >= n) { 27 throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1)); 28 } 29 } 30 31 32 public boolean connected(int p, int q) { 33 validate(p); 34 validate(q); 35 return id[p] == id[q]; 36 } 37 38 39 public void union(int p, int q) { 40 validate(p); 41 validate(q); 42 int pID = id[p]; 43 int qID = id[q]; 44 45 46 if (pID == qID) return; 47 48 for (int i = 0; i < id.length; i++) 49 if (id[i] == pID) id[i] = qID; 50 count--; 51 } 52 }
算法分析:
find()的操作是非常快的,因为他只需要访问数组一次,但是对于大型问题,这种算法很难处理,因为每次调用union()都要扫描整个数组。这种算法是平方级别的。
他和quick-find算法可以看作是互补的 ,不同之处在于quick-find的id[]数组中的元素是同一分量中的另一个触点(也有可能是它自己)--我们将这种联系称为链接。在find()方法中,我们从给定的触点开始,由他的链接得到另一个触点,以此类推,直到到达一个根触点(自己指向自己的触点,他一定会存在,因为我们在初始化的时候每个触点都指向自己)。
当且仅当分别由两个触点到达了同一根触点时他们存在于同一连通分量中。我们由p和q的链接去找到他们的根触点,然后只需要将其中的一个根触点链接到另一个根触点即可。
代码实现:

1 public class QuickUnion { 2 private int[] parent; 3 private int count; 4 5 6 public QuickUnion(int n) { 7 parent = new int[n]; 8 count = n; 9 for (int i = 0; i < n; i++) { 10 parent[i] = i; 11 } 12 } 13 14 15 public int count() { 16 return count; 17 } 18 19 20 public int find(int p) { 21 validate(p); 22 while (p != parent[p]) 23 p = parent[p]; 24 return p; 25 } 26 27 28 private void validate(int p) { 29 int n = parent.length; 30 if (p < 0 || p >= n) { 31 throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1)); 32 } 33 } 34 35 36 public boolean connected(int p, int q) { 37 return find(p) == find(q); 38 } 39 40 41 42 public void union(int p, int q) { 43 int rootP = find(p); 44 int rootQ = find(q); 45 if (rootP == rootQ) return; 46 parent[rootP] = rootQ; 47 count--; 48 } 49 }
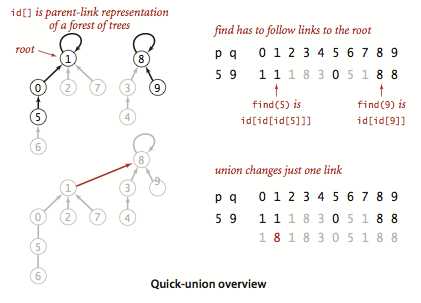
左图为处理右图的部分轨迹。
处理数据为
10
4 3
3 8
6 5
9 4
2 1
8 9
5 0
7 2
6 1
1 0
6 7
算法分析:
quick-union算法看起来比quick-find算法要快,因为它不需要遍历整个数组,而实际上它的时间成本更依赖于输入的特点,在最坏的情况下仍然是平方级别的,例如如果最后都连接成了一个连通分量,那么考虑这种情况输入的是0-1,0-2,0-3等,其中0链接到1,1链接到2,2链接到3……,如果此时在输入0-(N-1),处理这N个整数find方法需要访数组的次数为平方级别。(假设现在还剩两个连通分量,其中一个含有N-1个触点,一个含有1个触点,而我们写的算法可能会将大的连通分量链接到小的连通分量的根触点上,这样就会浪费时间)
我们不是在quick-union中任意将一个树连接到另一个树,而是跟踪每个树的大小,并始终将较小的树连接到较大的树。这项操作需要添加一个数组来记录各个连通分量的触点的个数。
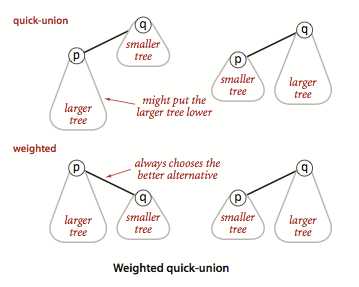
代码实现:

1 public class WeightedQuickUnion { 2 private int id[]; 3 private int sz[]; 4 private int count;//连通分量个数 5 public WeightedQuickUnion(int n) 6 { 7 count=n; 8 id=new int[n]; 9 for(int i=0;i<n;i++) 10 { 11 id[i]=i; 12 } 13 14 sz=new int[n]; 15 for(int i=0;i<n;i++) 16 { 17 sz[i]=1; 18 } 19 20 } 21 public int count() 22 { 23 return count; 24 } 25 26 private void validate(int p) 27 { 28 int n = id.length; 29 if (p < 0 || p >= n) { 30 throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1)); 31 } 32 } 33 34 public boolean connected(int p,int q) 35 { 36 validate(p); 37 validate(p); 38 return find(p)==find(q); 39 40 } 41 public int find(int p) 42 { 43 validate(p); 44 while(p!=id[p]) 45 p=id[p]; 46 return p; 47 } 48 public void union(int p,int q) 49 { 50 validate(p); 51 validate(p); 52 int i=find(p); 53 int j=find(q); 54 if(i==j) return; 55 if(sz[i]<sz[j]) 56 { 57 id[i]=j; 58 sz[j]+=sz[i]; 59 } 60 else 61 { 62 id[j]=i; 63 sz[i]+=sz[j]; 64 } 65 count--; 66 } 67 }
算法分析:
我们考虑一下最坏的情况,要归并的两个树的大小总是相等的,且总是2的幂,这样的树高度总为n,当归并时,得到的树含有2的(n+1)次幂个节点,高度为n+1.这样可以看出这种算法总是具有对数级别的性能,这种算法也是以上三种算法中唯一一种能处理大型问题的算法。
标签:部分 说明 || not 相同 多个 opened cte nbsp
原文地址:https://www.cnblogs.com/lls101/p/11218986.html