RPG游戏中Bresenham算法推导以及应用

标签：就是   条件   图片   过程   step   应用   function   参数   情况   

先来看一种dda算法：
function dda(x0: number, y0: number, x1: number, y1: number) {
let output = [];
let k = (y1 - y0) / (x1 - x0);
let x = x0 + 1; //x初始值
while (x <= x1) {
let y = Math.floor(k * (x + 1) + 0.5);
output.push({ x: x, y: y });
x = x + 1;
}
return output;
}
代码很少，但是运算中用到了浮点数的乘法和加法，不是一种高效的做法。

接着来看下bresenham算法的推导过程。
Bresenham算法有2种推导方法，如下图所示: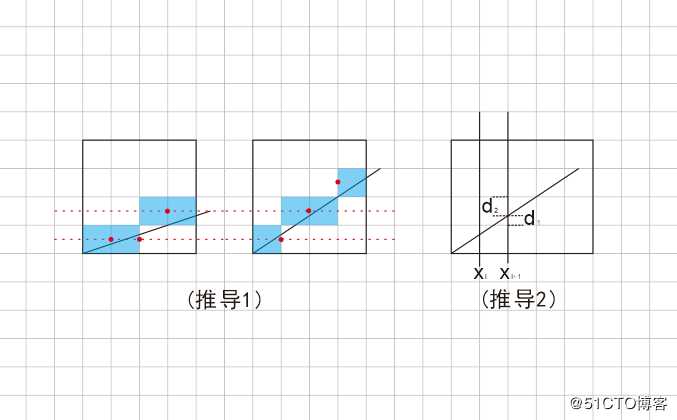

为了简单起见，设，直线方程为y = kx，也就是以起始点为坐标原点。

1. 设置变量，xStep = 1；totalXstep = 0；totalYstep = 0；lineY = 0；gridY = 0；preGridY = 0；deltaX = x1-x0；deltaY= y1-y0。其中lineY为直线上真实的纵坐标，girdY为选择的格子坐标，preGridY为上一个格子坐标。
2. 由y = kx可知道，当x每增加1，y的增量为k。
3. 由x0开始推导。
   A．当x = x0 + 1，totalXstep = totalXstep +1，lineY = y0 + k，判别式为k-0.5。
   当k - 0.5 >= 0时，gridY = y0 + 1，totalYstep = totalYstep + 1；
   当k – 0.5 < 0时，gridY = y0；
   preGridY= gridY；
   B．当x = x0 + 2，totalXStep = totalXStep + 1，lineY =y0 + totalXstep k，判别式为 totalXstep k – (totalYstep + 0.5);
   当totalXstep k – (totalYstep + 0.5) >=0时，gridY = preGridY +1，totalYstep = totalYstep + 1；
   当totalXstep k – (totalYstep + 0.5) < 0时，gridY = preGridY，
   preGridY= gridY；
4. 由上可得，判别式为totalXstep k – (totalYstep + 0.5) >=0，k = deltaY / deltaX；将k代入左式，并且两边乘以deltaX，再乘以2得:
   2totalXstep deltaY –2deltaXtotalYstep – deltaX >=0
   也可以写成：
   2totalXstep deltaY > 2deltaX*totalYstep + deltaX
   由此，这个算法只剩下整数的乘法和加法。

下面我们换另外一种推导方法。
1.设置变量d1，d2，Xi，Xi+1，Yi，Yi+1，Y，X，Hi，Hi+1

2. d1 = Y- Yi =(k(Xi +1) + b) –Yi
   d2 = Yi +1 - Yi = Yi +1 -(k(Xi +1) + b)
3. d1-d2 = 2k(Xi +1) – 2 Yi +2b-1
   4.将k = deltaY/deltaX，代入上式得
   deltaX(d1-d2) = 2deltaY Xi -2deltaX Yi + c
   令Hi = deltaX(d1-d2) = 2deltaY Xi -2deltaX Yi + c
   则Hi+1 = 2deltaY Xi+1 -2deltaX Yi+1 + c
   Hi+1 - Hi = 2deltaY( Xi+1 - Xi) – 2deltaX( Yi+1 - Yi)
   令Xi+1 = Xi +1，
   Hi+1 = Hi +2deltaY – 2deltaX( Yi+1 - Yi)
   则：
   A． 如果选择右上方的像素，即：Yi+1 – Yi =1， 则 Hi+1 = Hi +2deltaY – 2deltaX
   B．如果选择右方像素，即Yi+1 = Yi ，则：Hi+1 = Hi +2deltaY
   在起始像素(x0,y0)的第一个参数h0为：
   h0 = 2deltaY – deltaX；
   这个算法只会用到较为快速的整数加法、减法和位元移位，是高效的算法。
   function bresenham(x0: number, y0: number, x1: number, y1: number) {
   let output = [];
   let deltaX = x1 - x0;
   let deltaY = y1 - y0;
   let err = 2 deltaY - deltaX;
   let x = x0;
   let y = y0;
   while (x <= x1) {
   x++;
   //先假设取右方的点，说明err+2deltaY小于0；
   // 其实也可以假设取右上方的点，判断条件要不同
   err = err + 2 deltaY;
   if (err >= 0) { //说明取右方的点是不对的，应取右上方的点
   y++;
   err = err - 2 * deltaX;
   }
   output.push({ x: x, y: y });
   }
   }

RPG游戏中Bresenham算法推导以及应用

标签：就是   条件   图片   过程   step   应用   function   参数   情况   

原文地址：https://blog.51cto.com/zhangzhao/2422258