标签:dash const bool tchar mda 它的 return 操作 http
这些天,兔兔和蛋蛋喜欢上了一种新的棋类游戏。 这个游戏是在一个n行m列的棋盘上进行的。游戏开始之前,棋盘上有一个格子是空的,其它的格子中都放置了一枚棋子,棋子或者是黑色,或者是白色。 每一局游戏总是兔兔先操作,之后双方轮流操作,具体操作为:
兔兔每次操作时,选择一枚与空格相邻的白色棋子,将它移进空格。
蛋蛋每次操作时,选择一枚与空格相邻的黑色棋子,将它移进空格。
第一个不能按照规则操作的人输掉游戏。为了描述方便,下面将操作“将第x行第y列中的棋子移进空格中”记为M(x,y)。 例如下面是三个游戏的例子。
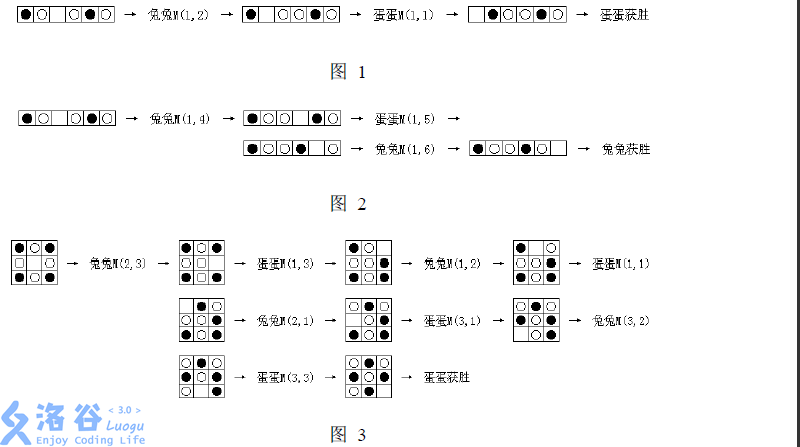
最近兔兔总是输掉游戏,而且蛋蛋格外嚣张,于是兔兔想请她的好朋友——你——来帮助她。她带来了一局输给蛋蛋的游戏的实录,请你指出这一局游戏中所有她“犯错误”的地方。 注意:
两个格子相邻当且仅当它们有一条公共边。
兔兔的操作是“犯错误”的,当且仅当,在这次操作前兔兔有必胜策略,而这次操作后蛋蛋有必胜策略。
这题显然可以转化成一个二分图模型
在一个二分图中,从给定的起点u开始移动棋子,两个玩家轮流移动,不得经过重复的点,若一方无法移动即为输家
1 #include <cstdio> 2 #include <iostream> 3 #include <cstring> 4 #include <vector> 5 #define N 2510 6 using namespace std; 7 const int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0}; 8 int n,m,k,sx,sy,a[50][50],vis[N],p[N]; 9 vector<int> q[N],ans; 10 bool bz[N],b[N]; 11 bool dfs(int x) 12 { 13 if (bz[x]) return 0; 14 for (int i=0;i<q[x].size();i++) 15 { 16 int y=q[x][i]; 17 if (!bz[y]&&!vis[y]) 18 { 19 vis[y]=1; 20 if (!p[y]||dfs(p[y])) { p[y]=x,p[x]=y; return 1; } 21 } 22 } 23 return 0; 24 } 25 int main() 26 { 27 scanf("%d%d",&n,&m); 28 for (int i=1;i<=n;i++) 29 for (int j=1;j<=m;j++) 30 { 31 char ch=getchar(); while (ch!=‘X‘&&ch!=‘O‘&&ch!=‘.‘) ch=getchar(); 32 a[i][j]=(ch==‘O‘)?1:2; if (ch==‘.‘) sx=i,sy=j; 33 } 34 for (int i=1;i<=n;i++) 35 for (int j=1;j<=m;j++) 36 for (int k=0;k<4;k++) 37 { 38 int xx=i+dx[k],yy=j+dy[k]; 39 if (xx<1||xx>n||yy<1||yy>m) continue; 40 if (a[i][j]!=a[xx][yy]) q[(i-1)*m+j].push_back((xx-1)*m+yy); 41 } 42 for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) if (a[i][j]==2) memset(vis,0,sizeof(vis)),dfs((i-1)*m+j); 43 scanf("%d",&k); 44 for (int i=1,x,y;i<=k*2;i++) 45 { 46 x=(sx-1)*m+sy,bz[x]=1; 47 if (p[x]) y=p[x],p[x]=p[y]=0,memset(vis,0,sizeof(vis)),b[i]=!dfs(y); 48 scanf("%d%d",&sx,&sy); 49 } 50 for (int i=1;i<=k;i++) if (b[i*2-1]&&b[i*2]) ans.push_back(i); 51 printf("%d\n",ans.size());; 52 for (int i=0;i<ans.size();i++) printf("%d\n",ans[i]); 53 }
标签:dash const bool tchar mda 它的 return 操作 http
原文地址:https://www.cnblogs.com/Comfortable/p/11224751.html